Применение производной при исследовании функций

Пределы и производные удобно применять к исследованию функций и построению графиков.

Общая схема исследования функций и построения их графиков:

1. Найти область определения функции.

2. Найти точки разрыва функции и ее односторонние пределы в этих точках.

3. Выяснить, является функция четной, нечетной или периодиче­ской.

4. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.

5. Найти асимптоты графика функции:

а) вертикальные;

б) невертикальные.

6. Найти точки экстремума и интервалы возрастания и убывания функции.

7. Найти точки перегиба графика функции и интервалы его выпук­лости и вогнутости.

8. Построить график функции, используя все полученные результаты исследования.

Рассмотрим отдельно некоторые пункты исследования.

Асимптотой кривой называется такая прямая, к которой неограни­ченно приближается точка кривой при неограниченном удалении этой точки от начала координат.

Для нахождения асимптот пользуются следующими положениями:

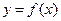а) если при кривая имеет бесконечный разрыв, т.е. если при слева или справа функция стремится к бес­конечности (того или иного знака), то прямая является ее верти­кальной асимптотой;

б) невертикальные асимптоты кривой 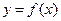, если они сущест­вуют, имеют уравнения вида , где параметры и опреде­ляются формулами:

Пример. Найти асимптоты кривой .

Решение:

а) при кривая имеет бесконечный разрыв. Поэтому прямая есть вертикальная асимптота. Найдем односторонние пределы:

- слева

- справа

Значит, при стремлении 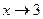слева функция неограниченно воз­растает, а справа - неограниченно убывает;

б) найдем невертикальные асимптоты:

Уравнение невертикальной, наклонной асимптоты будет

Других невертикальных асимптот кривая не имеет, так как при значения 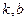будут те же самые.

Возрастание и убывание функции 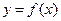характеризуется зна­ком ее производной : если в некотором интервале , то функция возрастает, а если , то функция убывает в этом интервале.

Значение функции в точке 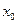называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравне­нию с ее значениями во всех достаточно близких точках слева и справа от 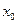. Функция может иметь экстремум (максимум или мини­мум) только в тех точках, которые лежат внутри области определения функции и где ее первая производная равна нулю или не существует. Такие точки называются критическими.

Функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна.

Из определений вытекает правило исследования функции на экстре­мум:

1. Найти производную и критические точки, лежащие внутри области определения функции.

2. Определить знак слева и справа от каждой критической точки. Если при переходе аргумента 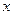через критическую точку :

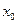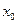1) меняет знак с + на -, то есть точка максимума;

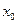2) меняет знак с - на +, то есть точка минимума;

3) не меняет знак, то в этой точке нет экстремума.

Для исследования критических точек, где , можно также рас­смотреть знак второй производной:

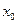1) если , то есть точка минимума;

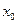2) если , то есть точка максимума;

3) если , то характер точки 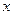можно выяснить только по изменению знака этой точки.

Пример. Найти интервалы монотонности функции и точки экстремума.

Область определения функции есть множество всех действительных чисел.

Полагая , получим 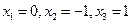. Других кри­тических точек нет.

Исследуем критические точки по изменению знака первой произ­водной. Составим таблицу:

	+		+		-		-
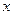
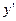
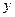
	возрастает	нет экстр.	возрастает	максимум	убывает	нет экстр.	убывает

В первой строке размещены критические точки и интервалы моно­тонности функции. Во второй - знаки производной в интервалах и значе­ния в критических точках. В третьей - выводы о поведении функции.

Соответственно результатам исследования функция возрастает на интервале и убывает на интервале . Точка есть точка максимума.

Если в некотором интервале кривая расположена ниже любой своей касательной, то кривая называется выпуклой, а если она расположена выше любой своей касательной, то вогнутой.

Точкой перегиба называется точка на кривой, разделяющая области выпуклости и вогнутости.

Характер кривой 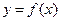определяется знаком второй производ­ной : если в некотором интервале , то кривая вогнутая, а если , то кривая выпуклая.

Нахождение точек перегиба и интервалов выгнутости и выпуклости сводится к следующему:

1. Найти вторую производную . В области определения функции и непрерывности кривой найти точки 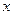, в которых или не суще­ствует.

2. Определить знак слева и справа от каждой из этих точек. Ис­следуемая точка 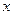будет абсциссой точки перегиба, если по разные сто­роны от нее имеет разные знаки.

Интервалы выпуклости и вогнутости кривой определяются из усло­вия, что их границами могут быть только точки перегиба, точки разрыва и граничные точки области расположения кривой.

Пример. Найти точки перегиба и интервалы выпуклости и вогнутости кривой .

Область определения функции есть множество всех действительных чисел.

точках

Других точек, которые могут быть абсциссами точек перегиба, нет.

Исследуем найденные точки, определяя знак слева и справа от каждой из них. Составим таблицу:

	+		-		+
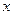
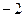
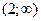
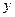
	вогнута	т.перегиба	выпукла	т.перегиба	вогнута

Рассмотрим пример полного исследования функции и построения ее графика.

1. Функция определена и непрерывна на всей оси за исключением точек .

2. Определим односторонние пределы в точках разрыва:

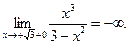
Значит, точки есть точки бесконечного разрыва.

3. Функция нечетная, т.к. .

Ее график симметричен относительно начала координат.

4. При 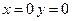, т.е. график функции проходит через начало координат. Интервалы оси , в которых функция сохраняет постоян­ный знак:

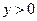- здесь ; - здесь

В силу симметрии графика функции:

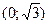- здесь 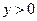; 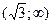- здесь

5. Прямые и есть вертикальные асимптоты графика. В соответствии с результатами п.2 при слева функ­ция неограниченно возрастает, а при стремлении справа неограниченно убывает. Аналогично поведение функции вблизи точки

Определим невертикальные асимптоты

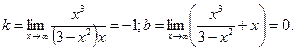
Те же значения коэффициентов при . Заключаем, что график исследуемой функции имеет невертикальную асимптоту .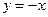

6. Найдем интервалы возрастания и убывания функции и точки экс­тремума:

Приравняем числитель выражения к нулю в найдем критические точки:

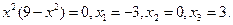
Производная может менять знак при переходе аргумента через эти точки и точки разрыва 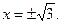Составим таблицу:

	-		+		+		+		+		-
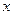
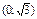
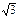
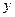
	убывает	миним.	возрастает	т.разр	возрастает	нет экстр	возрас-тает	т.разр	возрас- тает	макс.	убы-вает

Таким образом, при функция имеет минимум, а при - максимум. Определим ординаты точек экстремума:

7. Найти интервалы выпуклости и вогнутости графика функции и
точки перегиба:

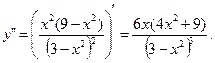
Видно, что только при . Вторая производная может менять знак только в этой точке и точках разрыва. Составим таблицу:

	+		-		+		-
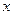
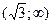
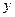
	вогнута	т.разрыва	выпукла	т.перегиба	вогнута	т.разрыва	выпукла

Значит, - абсцисса точки перегиба.

8. Все результаты исследования используем для построения графика.

Вычерчивание графика следует начинать с нанесения на плоскость его асимптот, затем точек экстремума и перегиба данной функции. Знание интервалов возрастания и убывания функции, выпуклости и вогнутости, а также поведение функции вблизи асимптот помогут вычертить график осмысленно и точно.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: