 |
Наибольшее и наименьшее значения функции на отрезке
|
|
|
|
Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
если в некотором интервале (конечном или бесконечном) функция  непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале;
непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале;
если функция  непрерывна на некотором отрезке
непрерывна на некотором отрезке  , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
Таким образом, для нахождения наибольшего и наименьшего значений функции  на отрезке
на отрезке  следует:
следует:
1. Найти критические точки, лежащие внутри отрезка  и вычислить значения функции в этих точках.
и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка, т.е.  и
и  .
.
3. Из всех полученных значений функции выбрать наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке  .
.
Решение:
1. Найдем критические точки функции 
 при
при 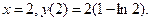 Других критических точек внутри данного отрезка нет.
Других критических точек внутри данного отрезка нет.
2. Вычислим значения функции на концах отрезка: 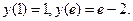
3. Сравним полученные значения: 
Таким образом, наибольшее значение функции  а наименьшее –
а наименьшее – 
Контрольная работа №3 по теме
«Введение в анализ.
Дифференциальное исчисление функции
Одной переменной»
3.1 Найти пределы:
3.1.1а)  б)
б) 
в)  г)
г) 
д)  е)
е) 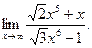
3.1.2 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.3 а)  б)
б) 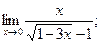
в)  г)
г) 
д)  е)
е) 
3.1.4 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.5 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.6 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.7 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.8 а)  б)
б) 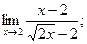
в)  г)
г) 
д)  е)
е) 
3.1.9 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.1.10 а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
3.2. Найти производные
3.2.1. а)  б)
б)  ;
;
в)  ; г)
; г)  ;
;
д) 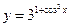 ; е)
; е)  ;
;
ж)  ;
;
3.2.2. а)  ; б)
; б)  ;
;
|
|
|
в)  ; г)
; г) 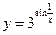 ;
;
д)  ; е)
; е)  ;
;
ж)  ;
;
3.2.3. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ;
;
3.2.4. а)  ; б)
; б) 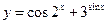 ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж) 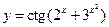 ;
;
3.2.5. а) 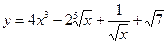 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 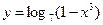 ;
;
ж)  ;
;
3.2.6. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ;
;
3.2.7. а)  ; б)
; б)  ;
;
в) 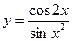 ; г)
; г)  ;
;
д) 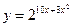 ; е)
; е)  ;
;
ж)  ;
;
3.2.8. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж) 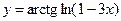 ;
;
3.2.9. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ;
;
3.2.10. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ;
;
3.3. Найти производную
3.3.1.  ; 3.3.2.
; 3.3.2.  ;
;
3.3.3.  ;
;
3.3.4.  ;
;
3.3.5.  ; 3.3.6.
; 3.3.6.  ;
;
3.3.7.  ; 3.3.8.
; 3.3.8.  ;
;
3.3.9.  ; 3.3.10.
; 3.3.10.  ;
;
3.4. Найти производную
3.4.1.  ; 3.4.2.
; 3.4.2.  ;
;
3.4.3.  ; 3.4.4.
; 3.4.4.  ;
;
3.4.5.  ; 3.4.6.
; 3.4.6.  ;
;
3.4.7.  ; 3.4.8.
; 3.4.8.  ;
;
3.4.9.  ; 3.4.10.
; 3.4.10.  ;
;
3.5. Найти производную
3.5.1.  ; 3.5.2.
; 3.5.2.  ;
;
3.5.3.  ; 3.5.4.
; 3.5.4.  ;
;
3.5.5.  ; 3.5.6.
; 3.5.6.  ;
;
3.5.7.  ; 3.5.8.
; 3.5.8.  ;
;
3.5.9.  ; 3.5.10.
; 3.5.10.  ;
;
3.6.1. Записать уравнение касательной к линии  в точке с абсциссой
в точке с абсциссой  .
.
3.6.2. Выяснить, в какой точке кривой 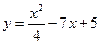 касательная параллельна прямой
касательная параллельна прямой  .
.
3.6.3. Записать уравнение нормали к линии  в точке с абсциссой
в точке с абсциссой  .
.
3.6.4. Выяснить, в какой точке кривой  касательная перпендикулярна прямой
касательная перпендикулярна прямой 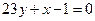 .
.
3.6.5. Найти, какой угол образует с осью обсцисс касательная к параболе  в т.
в т.  .
.
3.6.6. Записать уравнение касательной к кривой  в точке с ординатой
в точке с ординатой  .
.
3.6.7. Записать уравнение нормали к кривой  в точке с ординатой
в точке с ординатой  .
.
3.6.8. Определить угловой коэффициент касательной к кривой  в точке
в точке  .
.
3.6.9. В какой точке кривой  касательная перпендикулярна к прямой
касательная перпендикулярна к прямой  .
.
3.6.10.Выяснить, в какой точке кривой  касательная составляет с осью
касательная составляет с осью  угол
угол  .
.
3.7.1. Траектория движения тела – кубическая парабола  . В каких ее точках скорость возрастания абсциссы и ординаты одинаковы?
. В каких ее точках скорость возрастания абсциссы и ординаты одинаковы?
3.7.2. Закон движения материальной точки  . В какой момент времени скорость ее движения будет равна 2 м/с?
. В какой момент времени скорость ее движения будет равна 2 м/с?
3.7.3. Тело движется по прямой  по закону
по закону  . Определить скорость и ускорение движения тела.
. Определить скорость и ускорение движения тела.
3.7.4. Тело, брошенное вверх, движется по закону  . В какой момент времени скорость тела станет равна нулю? Найти наибольшую высоту подъема тела.
. В какой момент времени скорость тела станет равна нулю? Найти наибольшую высоту подъема тела.
3.7.5. Скорость тела, движущегося прямолинейно, определяется формулой  . Какое ускорение будет иметь тело через 4 с? После начала движения?
. Какое ускорение будет иметь тело через 4 с? После начала движения?
3.7.6. Тело массой 100 кг движется прямолинейно по закону  . Определить кинетическую энергию
. Определить кинетическую энергию  тела через 5 с после начала движения.
тела через 5 с после начала движения.
|
|
|
3.7.7. Заряд, проходящий через проводник, начиная с момента времени  , определяется формулой
, определяется формулой  . В какие моменты времени сила тока в проводнике будет равна нулю?
. В какие моменты времени сила тока в проводнике будет равна нулю?
3.7.8. Тело массой 6 т движется прямолинейно по закону. Требуется вычислить кинетическую энергию  тела через 1 с после начала движения.
тела через 1 с после начала движения.
3.7.9. Зависимость пути от времени при прямолинейном движении точки  . Найти скорость и ускорение через 1 секунду после начала движения.
. Найти скорость и ускорение через 1 секунду после начала движения.
3.7.10.Тело движется по прямой  согласно закону
согласно закону  . Определить скорость и ускорение движения. В какие моменты тело меняет направление движения?
. Определить скорость и ускорение движения. В какие моменты тело меняет направление движения?
3.8. Найти дифференциал функции:
3.8.1.  ; 3.8.2.
; 3.8.2.  ;
;
3.8.3. 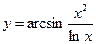 ; 3.8.4.
; 3.8.4.  ;
;
3.8.5.  ; 3.8.6.
; 3.8.6.  ;
;
3.8.7.  ; 3.8.8.
; 3.8.8.  ;
;
3.8.9.  ; 3.8.10.
; 3.8.10. 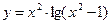 ;
;
3.9. Исследовать функцию и построить график
3.9.1.  ; 3.9.2.
; 3.9.2.  ;
;
3.9.3.  ; 3.9.4.
; 3.9.4. 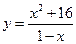 ;
;
3.9.5.  ; 3.9.6.
; 3.9.6. 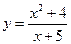 ;
;
3.9.7.  ; 3.9.8.
; 3.9.8.  ;
;
3.9.9.  ; 3.9.10.
; 3.9.10.  ;
;
3.10. Найти наибольшее и наименьшее значения функции на отрезке
3.10.1.  ; 3.10.2.
; 3.10.2.  ;
;
3.10.3.  ; 3.10.4.
; 3.10.4.  ;
;
3.10.5.  ; 3.10.6.
; 3.10.6.  ;
;
3.10.7.  ; 3.10.8.
; 3.10.8.  ;
;
3.10.9. 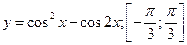 ; 3.10.10.
; 3.10.10.  ;
;
Контрольные вопросы к экзамену
1. Определение предела функции в точке.
2. Вычисление пределов элементарных функций в точке, принадлежащей области определения.
3. Виды неопределенностей и способы их раскрытия.
4. Первый и второй замечательные пределы.
5. Понятие бесконечно малой величины. Сравнение бесконечно малых.
6. Основные свойства пределов.
7. Применение понятия бесконечно малой для вычисления пределов.
8. Определение непрерывной функции в точке.
9. Определение производной, её геометрический и механический смысл.
10. Связь понятий непрерывности и дифференцируемости.
11. Основные правила нахождения производных. Производная сложной функции.
12. Таблицы основных производных.
13. Дифференциал функции и его геометрический смысл.
14. Производные и дифференциалы высших порядков: определения, нахождение.
15. Правило Лопиталя и его применение к вычислению пределов.
16. Применение пределов и производных к исследованию функций и построению их графиков. (Промежутки возрастания и убывания, выпуклости и вогнутости, точки экстремума, точки перегиба, асимптоты).
|
|
|


