 |
Метод математической индукции.
|
|
|
|
Принцип математической индукции.
Пусть некоторое А является подмножеством 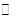 , которое удовлетворят следующим условиям:
, которое удовлетворят следующим условиям:
1. 
2. если  , то
, то  , тогда А содержит все натуральные числа, т.е.
, тогда А содержит все натуральные числа, т.е. 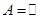 .
.
Доказательство:
Предположим, что утверждение теоремы не имеет место, т.е. теорема  . Рассмотрим дополнение множества А относительно множества
. Рассмотрим дополнение множества А относительно множества 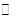 , т.е.
, т.е.  .
.
- По условию
 , причём
, причём  . По предположению
. По предположению  , т.е.
, т.е. 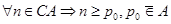 .
. - Если
 , кроме того
, кроме того  , то тогда
, то тогда  , а т.к.
, а т.к. 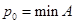 , т.е.
, т.е.  , т.к.
, т.к.  , где
, где  .
. - Пусть
 , согласно условию теоремы 2, тогда
, согласно условию теоремы 2, тогда  и
и  - противоречие, т.е.
- противоречие, т.е.  наше предположение не верно, следовательно,
наше предположение не верно, следовательно, 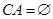 , т.е.
, т.е.  и т.д.
и т.д.
Пример: докажем, что  имеет место равенство
имеет место равенство  .
.
Доказательство: пусть  . Заметим, что при
. Заметим, что при 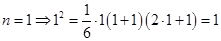 , т.е.
, т.е.  .
.
Если  , то
, то 
 в силу принципа математической индукции имеем, что
в силу принципа математической индукции имеем, что  , т.е. наша формула справедлива
, т.е. наша формула справедлива  .
.
Так же предлагаем более доступный вариант объяснения Метода Математической индукции.
ПОНЯТИЕ ПОЛНОЙ И НЕПОЛНОЙ ИНДУКЦИИ.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ.
1. Индукцией называется метод рассуждений, ведущий от частных примеров к некоторому общему выводу (индукция – латинское слово Inductio, означающее «наведение»).
При доказательстве математических предложений различают неполную индукцию, полную индукцию и математическую индукцию.
2. Неполной индукцией называется метод рассуждений, при котором общий вывод делается на основе рассмотрения достаточно большого числа примеров, которые не охватывают всехвозможныхслучаев.
Метод неполной индукции (нельзя признать методом строго доказательства) позволяет сформулировать гипотезу (гипотеза от греческого hypöthesis – основание, предположение), которую можно доказать или опровергнуть с помощью других методов доказательства.
|
|
|
3. Полной индукцией называется метод рассуждений, при котором общий вывод делается на основании разбора всех частных случаев.
Этот метод применим лишь для конечного числа случаев, причем он целесообразен для не слишком большого их числа.
Пример1:
Доказать, что при  -х
-х  справедливо высказывание:
справедливо высказывание:  .
.
Решение:
При доказательстве надо учитывать, что данное высказывание образованно с помощью логической операции «или» (меньше или равно), а такое высказывание истинно, если истинно хотя бы одно из высказываний  или
или  .
.
Рассмотрим все возможные случаи:
1) Числа 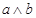 имеют одинаковые знаки, т.е.
имеют одинаковые знаки, т.е. 

 . И в том
. И в том  в другом случае для нахождения модуля суммы
в другом случае для нахождения модуля суммы 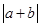 надо сложить модули слагаемых. Тогда высказывание
надо сложить модули слагаемых. Тогда высказывание  справедливо, т.к.
справедливо, т.к.  .
.
2) Числа 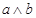 имеют разные знаки, т.е.
имеют разные знаки, т.е. 

 . В этом случае, чтобы найти модуль суммы, надо из большего модуля вычесть меньший. Пусть
. В этом случае, чтобы найти модуль суммы, надо из большего модуля вычесть меньший. Пусть  . Тогда
. Тогда  ; т.к. числа
; т.к. числа  положительны, то их разность меньше суммы; значит,
положительны, то их разность меньше суммы; значит,  и, следовательно, высказывание
и, следовательно, высказывание  истинно.
истинно.
3) Одно из чисел  равно нулю.
равно нулю.
Пусть  ,
,  - любое действительное число, в том числе
- любое действительное число, в том числе  нуль. В этом случае
нуль. В этом случае 

 ; следовательно
; следовательно  , что доказывает справедливость данного утверждения.
, что доказывает справедливость данного утверждения.
Аналогично с помощью полной индукции доказывается теорема «площадь параллелограмма равна произведению его основания на высоту».
Таким образом, метод полной индукции приводит к общему выводу после рассмотрения каждого из конечного числа возможных случаев. Этот метод рассуждений вполне надёжен.
4. Принцип математической индукции.
1) Если предложение  , в котором
, в котором 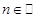 , истинно для
, истинно для  и из того, что оно истинно для
и из того, что оно истинно для  (где
(где  ), следует, что оно истинно и для следующего числа
), следует, что оно истинно и для следующего числа  , то предложение
, то предложение  истинно для
истинно для  -го
-го 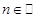 .
.
2) Доказательство методом математической индукции состоит из двух частей, основанных на указанном выше принципе:
a) В первой части доказывают (проверяют) истинность высказывания  .
.
b) Во второй части предполагают, что  верно для
верно для  и доказывают справедливость предложения
и доказывают справедливость предложения  для
для  , т.е. что
, т.е. что  .
.
|
|
|
Если обе части доказательства проведены, то на основании принципа математической индукции можно заключить, что предложение  истинно для
истинно для 
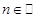 .
.
Символически формулировка метода математической индукции записывается так:
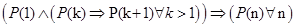 , где
, где 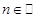 .
.
Примеры доказательств методом математической индукции
Пример 1. Доказать, что при 
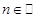 верно равенство
верно равенство
 (1)
(1)
Доказательство:
Обозначим данное высказывание через  , где
, где 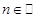 , а сумму в левой части (1) через
, а сумму в левой части (1) через  .
.
a) Высказывание  истинно, т.к. при
истинно, т.к. при  получаем верное равенство:
получаем верное равенство:  .
.
b) Предположим, что  верно для
верно для  ; тогда:
; тогда: 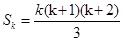 .
.
Докажем, что  , т.е.
, т.е.  . Имеем
. Имеем 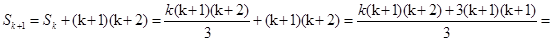
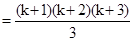 т.к.
т.к.  истинно
истинно 
 , то на основании принципа мат. индукции заключаем, что формула (1) справедлива для
, то на основании принципа мат. индукции заключаем, что формула (1) справедлива для 
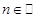 .
.
Пример 2. Методом математической индукции доказать, что

Доказательство:
a)  истинно, т.к. при
истинно, т.к. при  получаем верное равенство:
получаем верное равенство:  .
.
b) Предположим, что  верно для
верно для  ; тогда:
; тогда:  . Докажем, что
. Докажем, что  , т.е.
, т.е.  , т.е.
, т.е.  , т.к.
, т.к.  истинно и
истинно и  , то на основании приципа математической индукции заключаем, что
, то на основании приципа математической индукции заключаем, что  истинно для
истинно для  .
.
Замечание. Может случиться, что некоторые утверждения относительно натурального « » выполняются не при всех
» выполняются не при всех  , а начиная с какого-либо другого значения (
, а начиная с какого-либо другого значения (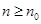 ). В этом случае можно пользоваться следующим видоизменением принципа индукции:
). В этом случае можно пользоваться следующим видоизменением принципа индукции:
Пусть о некотором утверждении  относительно натурального числа
относительно натурального числа  известно:
известно:
I. Утверждение  выполняется при
выполняется при  ;
;
II. Каким бы ни было натуральное  , из справедливости
, из справедливости  при
при  вытекает, что
вытекает, что  справедливо и при
справедливо и при  , т.е.
, т.е.  .
.
Тогда  выполняется при
выполняется при  натуральном
натуральном 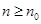 .
.
Можно показать, что это предположение эквивалентно принципу (аксиоме) мат. индукции.
Тогда метод математической индукции имеет вид:
 .
.
Пример 1.
Найти все 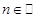 для которых
для которых  .
.
Решение: Имеем  при
при


Однако п ри 
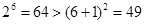 .
.
Докажем, что при  выполняется неравенство:
выполняется неравенство:  .
.
Для это установим, что при 
 (
( )
)
это неравенство эквивалентно неравенству 

 , что справедливо при
, что справедливо при 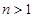 , и тем более при
, и тем более при  .
.
Допустим, что при некотором 
 (
( ).
).
Перемножаем формулы ( ) и (
) и ( ):
):


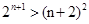 .
.
Ответ: 
Пример 2.
Доказать неравенство Бернулли:  , где
, где 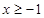 ,
,  .
.
Доказательство:
a) При  высказывание
высказывание  истинно:
истинно: 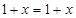 .
.
b) Нужно доказать, что при 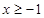 из предположения о справедливости неравенства:
из предположения о справедливости неравенства: 
 справедливость неравенства
справедливость неравенства  (
( ). Докажем этот факт.
). Докажем этот факт.
Если неравенство  является верным, то при умножении обеих частей на
является верным, то при умножении обеих частей на  , где
, где  , получим верное неравенство:
, получим верное неравенство:  , где
, где  , так как
, так как  мы его отбросили и усилии неравенство.
мы его отбросили и усилии неравенство.
|
|
|
Таким образом, при 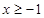 справедливо неравенство (
справедливо неравенство ( ) и поэтому неравенство
) и поэтому неравенство  является верным при
является верным при  .
.
|
|
|


