 |
Задачи на арифметическую прогрессию
|
|
|
|
Задача 1. В арифметической прогрессии дано: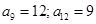 
. Определить 
.
Решение: 
Т.к. найти разность d можно было взяв и другие два элемента, возьмём такие, чтобы туда входил искомый элемент , т.е.
(т.к. 
.
Ответ: 
Задача 2. Известно, что в арифметической прогрессии 
. Определить 
.
Решение: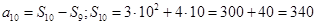 
.
Ответ: 
.
Задача 3. При какой зависимости между числами А, В, С они определяют собой 
члены одной и той же прогрессий.
Решение: запишем, что наши числа являются соответствующими числами арифметической прогрессии, получим систему
Исключим из этой системы 
и 
, т.к. они нам по условию задачи не нужны. Вычтем из первого равенство второе, а из второго – третье:
А теперь поделим четвертую формулу на пятую:
.
При таком соотношении между этими числами, они будут, соответственно, 5-м,8-м, 20-м членами одной и той же арифметической прогрессии. Если задать конкретные значения любым двум из 3 чисел, то третье число примет вполне определённое значение. Таким образом, таких прогрессий может быть неограниченное число.
Задача 4. Могут ли числа 
быть членами одной и той же арифметической прогрессии.
Решение:
Предположим, что могут быть, тогда возможны 2 случая:
Соотношение 
, конечно, должно быть рациональным. Однако, хорошо видно, что дробь 
является числом иррациональным. Наше предположение, что числа образуют арифметическую прогрессию не имеют смысла. Они не могут быть членами одной и той же прогрессии
Задача 5. Найти 
арифметической прогрессии, в которой 
Решение: по условию имеем:
- 
,
а отсюда следует 
, откуда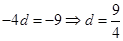 
.
Тогда 
и окончательно
Задача 6. В арифметической прогрессии 
Найти n.
Решение:
Отсюда: 
.
Тогда 
и 
. 
. Из равенства 
и находится значение 
.
|
|
|
Ответ: 
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Рекуррентная последовательность, у которой каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, называемое знаменателем прогрессии, носит название геометрической прогрессии. Условимся обозначать её - 
Таким образом, прогрессия является рекуррентной последовательностью, и её будем записывать так: 
.
Из определения 
член равен первому члену, умноженному на знаменатель прогрессии (
) в степени, показатель которой равен числу членов, предшествующих определяемому.
Мы получили первую формулу 
, её можно принять за определение прогрессии, где 
. - знаменатель прогрессии, 
. Если 
, то прогрессия называется возрастающей, если же 
, то называется убывающей. Значения - общий член прогрессии, где 
(
из рассмотрения исключается).
1) Используя метод математической индукции, докажем формулу общего члена прогрессии. По определению запишем:
Перемножаем все строчки: 
.
А теперь р азделив обе части равенства на произведение 
, имеем .
Доказательство полученной формулы.
I. При 
, получаем 
, т.е. Р(1) истинно.
II. Предположим, что истинно высказывание Р(
), т.е.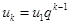 
.
III. Докажем, что в этом случае истинно и высказывание Р(
).
Имеем: 
, что и требовалось показать 
.
Итак, формула верна для .
2) Если все члены прогрессии положительны, то её член, начиная со второго, равен среднему геометрическому двух соседних членов, т.е. если 
, то 
.
В самом деле,
.
Иногда говорят: квадрат каждого члена прогрессии равен произведению двух равноудалённых от него членов этой прогрессии.
ч.т.д.
3) В каждой прогрессии произведение двух членов, равноотстоящих от концов, равно произведению крайних членов, т.е.:
Доказательство:
Произведение двух симметричных по отношению центра членов прогрессии есть величина постоянная для этой прогрессии, равная произведению крайних её членов.
|
|
|
4) Выведем формулу для знаменателя () (подобно формуле разности арифметической прогрессии. Разделим друг на друга произвольных два члена прогрессии:
.
|
|
|
