 |
Общие требования к проведению и оформлению курсовой работы
|
|
|
|
Содержание и требования к выполнению курсовой работы
Содержание курсовой работы
Курсовая работа состоит из двух логически связанных частей, соответствующих содержанию лекций, читаемых по дисциплине: «Методы оптимизации организационно-технических систем».
Первая часть работы посвящена аналитическим методам решения задач условной оптимизации целевых функций с ограничениями типа неравенств, накладываемых на векторный аргумент, то есть:
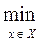 f (x) f (x)
| (1.1) |
Где х – вектор аргументов (параметров), имеющий в общем случае размерность [n´1], f(x) – скалярная унимодальная дифференцируемая функция, Х – множество допустимых значений аргументов х, заданное совокупностью ограничений типа неравенств:
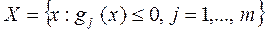
| (1.2) |
Где gj(x) - дифференцируемая функция векторного аргумента, j - число ограничивающих функций.
Задача (1.1) считается поставленной корректно, если ограничения gj(x)≤0, j=1,…,m совместимы и образуют непустое множество Х, на котором существует целевая функция f(x).
Аналитическое решение задачи (1.1, 1.2), конкретный вид которой определяется индивидуальным заданием по курсовой работе (см. раздел 3.1), осуществляется на основе теоремы Куна и Таккера (H.W. Kuhn, A.W. Tucker) о необходимых условиях минимума (максимума) целевой функции при ограничениях типа неравенств [1, 2]. Существо этой теоремы и построенный на ее основе алгоритм решения поставленной задачи излагаются в разделе 2.1.
В результате аналитического решения конкретной задачи типа (1.1, 1.2) каждым исполнителем должен быть получен набор локальных условных минимумов, из которых путем простого сравнения должен быть выбран глобальный условный минимум. Кроме того, полученное решение должно сопровождаться иллюстрацией целевой функции с отображенными на ней ограничениями типа неравенств и конкретных точек глобального и локальных условных минимумов. Это становится возможным поскольку целевая функция зависит только от двух переменных и может быть изображена в виде линий уровня с различными значениями функции на плоскости. На этом фоне относительно не трудно построить все конкретные ограничения и точки глобального и локальных условных минимумов. Для реализации этой иллюстрации предлагается использовать одну из известных графических программ, разработанных для ПЭВМ, например, в структуре “MATHCAD”.
|
|
|
Вторая часть работы посвящается применению наиболее эффективных численных методов безусловной оптимизации для решения задач условной оптимизации с ограничениями типа неравенств, то есть для решения задач, вписывающихся в общую постановку (1.1, 1.2).
В данном учебном пособии предлагается осуществить численное решение задачи условной оптимизации типа (1.1, 1.2) с помощью одного из часто используемых способов ее сведения к задаче безусловной оптимизации посредством метода «штрафных функций» [1, 2]. Методика применения этого метода достаточно подробно рассматривается в разделе 2.2, а общая процедура численного решения поставленной задачи должна осуществляться согласно следующему укрупненному алгоритму:
· применение метода «штрафных функций» - внешний цикл программы;
· применение одного из заданных численных методов безусловной оптимизации – внутренний цикл программы;
· применение одного из заданных численных методов одномерной оптимизации (если он входит в задание) – дополнительный цикл программы.
Состав задаваемых методов безусловной оптимизации определяется индивидуально при выдачи задания по курсовой работе. Их число, порядок и сложность численного метода зависят составлены таким образом, чтобы трудоемкости выполнения индивидуальных заданий были примерно одинаковыми как с точки зрения сложности конкретных численных методов, так и с точки зрения программирования, отладки и получения результатов счета на типовой ПЭВМ. В данной работе рассматриваются численные методы безусловной оптимизации, приведенные в классификации (см. раздел 2.2).
|
|
|
В процессе решения поставленной задачи с помощью задаваемых численных методов должны быть решены следующие подзадачи:
1. Разработка алгоритмов (блок-схем) и подпрограмм численных методов безусловной оптимизации, определенных индивидуальным заданием;
2. Разработка основной программы, в которой задаются все исходные данные, связанные с конкретной задачей условной оптимизации и фиксируются параметры соответствующих численных методов безусловной оптимизации;
3. Разработка подпрограммы, реализующей метод «штрафных функций», из которой происходит непосредственный вызов подпрограммы конкретного численного метода безусловной оптимизации;
4. Отладка и тестирование сформированной программы численного решения конкретной задачи условной оптимизации одним из заданных численных методов безусловной оптимизации (эта задача повторяется для каждого заданного метода отдельно);
5. Решение задачи условной оптимизации одним из заданных численных методов безусловной оптимизации (эта задача повторяется для каждого заданного метода отдельно);
6. Исследование влияния варьируемых параметров методов безусловной оптимизации (задаваемых в основной программе) на скорость сходимости к искомому решению, фиксируемому с заданной точностью;
7. Проведение сравнительного анализа заданных методов безусловной оптимизации по скоростям сходимости к искомому решению;
8. Написание выводов по проделанной работе.
Основные рекомендации по выполнению курсовой работы даются в разделе 2.
Общие требования к проведению и оформлению курсовой работы
Каждый студент получает индивидуальный вариант задания, в который включаются:
по части I работы - конкретные виды целевой функции, подлежащей минимизации, и ограничений типа неравенств;
по части II работы – численные методы безусловной оптимизации и методы одномерной оптимизации (если они входит в задание), с помощью которых необходимо решить (поочередно) поставленную задачу.
|
|
|
Процесс проведения курсовой работы строго регламентирован и должен выполняться согласно плану, представленному в табл 1.1. При этом задание по части II работы выдается только после выполнения части I.
Таблица 1.1
| № п/п | содержание | продолжитель-ность | основная литература |
| постановка конкретной задачи, оформление раздела в отчет по КР | 1 неделя | конспект лекций | |
| Изучение методики аналитического решения задачи, оформление раздела в отчет по КР | 1 неделя | [1, 2], конспект лекций и семинарских занятий | |
| решение задачи в черновом виде | 1 неделя | конспект семинарских занятий |
Продолжение Таблицы 1.1
| оформление части I КР, построение геометрической интерпретации результатов аналитического решения задачи | 1 неделя | конспект семинарских занятий | |
| Изучение методов численного решения задачи (согласно заданию), оформление раздела в отчет по КР | 1 неделя | [1, 2, 3], конспект лекций и семинарских занятий | |
| Формирование алгоритмов (блок-схем), программирование и отладка программного обеспечения | 1,5 недели | [1, 2, 3], конспект лекций и семинарских занятий | |
| Проведение численных исследований с помощью созданного программного обеспечения | 1,5 недели | ||
| Построение геометрической интерпретации результатов численного решения задачи и оформление части II отчета по КР | 0,5 недели | ||
| Анализ результатов и формулировка выводов по КР | 0,5 недели |
Как видно из плана проведения КР ее реализация рассчитана на ~ 9 недель, что составляет по продолжительности около 55 % семестра.
Отчет по КР должен быть оформлен согласно действующему ГОСТу на оформление научно-технических отчетов и удовлетворять следующим требованиям.
· Отчет по КР должен иметь титульный лист, на котором должны быть указаны: дисциплина, в рамках которой выполняется КР, учебное заведение, факультет и кафедра, где выполнялась КР, автор и руководители КР, а также год выполнения КР;
|
|
|
· Вслед за титульным листом Отчет по КР должен иметь лист - «Задание на КР», на котором компактно излагаются индивидуальные целевые функции, ограничения и численные методы, задаваемые преподавателем, контролирующим выполнение КР;
· Вслед за листом «Задание на КР» должно следовать Содержание отчета по КР;
· Часть I отчета по КР должна иметь раздел, посвященный общей и частной постановке задачи с привлечением принятой в данной дисциплине терминологии и математических обозначений;
должна иметь раздел, посвященный методике и алгоритму аналитического решения поставленной задачи (формализм Куна и Таккера);
должна иметь раздел, в котором описано (детально) конкретное решение поставленной задачи, оформленное согласно алгоритму аналитического решения;
· Часть II отчета по КР должна иметь раздел, посвященный описанию методики решения задач условной оптимизации численными методами безусловной оптимизации с помощью метода «Штрафных функций»;
должна иметь раздел, посвященный описанию алгоритмов (блок-схем) конкретных численных методов, определенных заданием;
должна иметь описание результатов численных исследований в виде соответствующих таблиц и графиков, а также графических изображений «траекторий» уменьшения целевой функции в процессе поиска условного минимума каждым численным методом;
· В заключении КР должны быть сформулированы выводы по проделанной исследовательской работе с учетом сравнительного анализа заданных численных методов безусловной оптимизации;
· В Приложении к КР должны быть помещены: распечатки модулей программного обеспечения, соответствующие блок-схемам заданных численных методов; результаты тестирования методов безусловной оптимизации; предложения по повышению эффективности заданных численных методов оптимизации.
|
|
|


