Методика аналитического решения задачи условной оптимизации с ограничениями типа неравенств

Для аналитического решения задачи типа (1.1, 1.2) предлагается использовать методику, в основе которой лежит теорема Куна и Таккера (H.W. Kuhn, A.W. Tucker) [1], представляющая собой в общем случае необходимые условия минимума целевой функции при наличии ограничений типа неравенств на множество допустимых значений векторного аргумента функции (см.(1.2)). В рассматриваемом приложении эту методику целесообразно представить в виде следующего расширенного алгоритма.

1. Формирование функции Лагранжа.

Исходя из обозначений принятых в постановке (1.1, 1.2), функция Лагранжа будет иметь вид:

F(x, l) = f (x) + lT g(x)

(2.1)

где l - вектор множителей Лагранжа размерности [m´1], соответствующей количеству ограничений g_j(x)≤0, j=1,…,m.

2. Применение необходимых условий (НУ) в форме Куна и Таккера для определения условных стационарных точек для задачи (1.1, 1.2).

В компактной форме для случая минимизации функции условия Куна и Таккера могут быть записаны в виде:

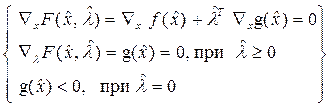
(2.2)

Где - координаты стационарных точек.

При рассмотрении конкретных задач, в которых количестве ограничений более одного, то есть при m >1 возможны различные сочетания активных и пассивных ограничений:

gi(x)=0, i Î I1; gj(x)<0, j Î I2

(2.3)

Где I₁ – множество номеров индексов активных ограничений, I₂ – множество номеров индексов пассивных ограничений (сумма элементов этих множеств всегда равна m).

Очевидно, что в этих случаях НУ (2.2) должны быть применены при всех возможных сочетаниях активных и пассивных ограничений, включая крайние случаи:

когда множество номеров активных ограничений I₁ пусто (l = 0), то есть фактически рассматривается задача безусловной оптимизации;

и когда количество активных ограничений, то есть количество элементов множества I₁ равно размерности вектора х – [n´1] (так называемые «угловые» точки), тогда эта точка фиксируется активными ограничениями и не допускает вариации целевой функции (имеется ввиду корректная постановка задачи (1.1, 1.2)).

В результате применения НУ для всех возможных сочетаний активных ограничений будут получены варианты стационарных точек - , в которых могут оказаться условные локальные минимумы и, в конечном итоге, - условный глобальный минимум, являющийся решением поставленной задачи.

3. Исключение всех стационарных точек, не удовлетворяющих пассивным ограничениям.

То есть:

gj()<0, j Î 1,m

(2.4)

4. Исключение стационарных точек, не удовлетворяющих условиям неотрицательности множителей Лагранжа.

Из оставшегося числа вариантов стационарных точек необходимо исключить все точки, не удовлетворяющие условиям неотрицательности соответствующих множителей Лагранжа - , в которых согласно НУ не могут находиться условные локальные минимумы целевой функции.

5. Проверка оставшихся стационарных точек на достаточные условия локального минимума функции.

Все оставшиеся стационарные точки, за исключением «угловых» точек, должны быть проверены с помощью достаточных условий (ДУ), подтверждающих или опровергающих наличие в них условного локального минимума.

Одним из широко распространенных вариантов ДУ нахождения в исследуемой стационарной точке условного локального минимума является положительная определенность матрицы Гессе, размера [n´n] (матрицы вторых частных производных) для функции Лагранжа F(х, l) по вектору х – [n´1].

H(x)(х, l) =

(2.5)

Известно, что матрица положительно определена, если составленная с ее помощью квадратичная форма положительно определена [1], то есть:

yTH(x)(х, l) y > 0

(2.6)

Где H (x) (х, l) - матрица Гессе (Гессиан) по вектору х; y – любой вектор с фиксированными значениями, размера [n´1].

Для проверки положительной определенности квадратичной формы (2.6) предлагается применить критерий Сильвестра [2, 4]. Суть его заключается в следующем.

Для того, чтобы квадратичная форма (2.6) была положительно определенной, необходимо и достаточно, чтобы матрица H (x) (х, l) имела все положительные угловые миноры, нарастающие вдоль главной ее диагонали, то есть были бы положительными определители матриц:

∆1 = h11> 0; ∆2 = > 0;…; ∆n = > 0

(2.7)

Где h_ij – элементы матрицы Гессе H (x) (х, l).

Таким образом, при подтверждении положительной определенности матрицы Гессе в стационарных точках, в которых согласно НУ возможно было нахождение условного локального минимума, то есть при 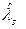> 0, такие стационарные точки переводятся в число точек условного локального минимума целевой функции f(x) при условиях gj(x) ≤ 0, j=1,…,m:

для номеров «s», удовлетворяющих НУ и ДУ

(2.8)

6. Определение условного глобального минимума.

Сравнение значений целевой функции f(x) в точках условного локального минимума и в «угловых» точках позволяет выявить условный глобальный минимум:

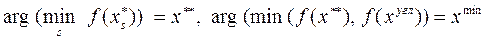
(2.9)

Где x^угл – координаты «угловых» точек, определяемых n активными ограничениями из числа jÎ1,…,m (см. пункт 2).

Таким образом условный глобальный минимум целевой функции равняется f(x_min).

В соответствии с требованиями к КР (см. раздел 1.2) полученный результат необходимо представить графически и прокомментировать его с помощью поясняющих подписей и отдельных пояснений, следующих после рисунка (масштаб рисунка должен выбираться из соображений его наглядности). Пример графического представления результата аналитического решения задачи типа (1.1, 1.2) изображен на рис. 2.1.

Рис	2.1

В частности, на рис. 2.1 изображены: целевая функция f(x) с помощью линий уровня C₁, C₂, C₃, …., причем C₁ < C₂ < C₃ и т.д.; ограничения g_j ≤ 0, j =1,2,3, выделяющие множество допустимых аргументов (параметров) - Х (запретные области условно заштрихованы); точки условного локального минимума определены номерами №1, №2, №3, №4, причем на рисунке видно, что точки №1 и №3 не удовлетворяют всем ограничениям g_j ≤ 0; «угловые» точки: №5, №6, №7.

Как следует из рассмотренной выше методики в результате сравнения значений функций в точках условного локального минимума №2, №4 и в «угловых» точках №5, №6, №7 определяются координаты условного глобального минимума, которые на рисунке обозначены №2.

1234	Поделиться:

Воспользуйтесь поиском по сайту: