 |
Бланк заданий «теста интеллекта»
|
|
|
|
| № | Инструкция | Задание |
| 1 | Выберите из приведенного списка лишнее слово и запишите его | Малиновый; желтый; сиреневый; лимонный |
| 2 | Запишите два слова, которые должны стоять на месте пропусков | Лондон: Англия = = Париж:... = =...: Италия |
| 3 | Закончите данное предложение | Из того, что Петя выше Толи, а Толя выше Оли, следует, что... |
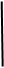     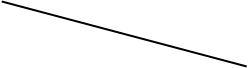   4 4
| Сколько треугольников изображено на рисунке? Правильный ответ обведите рамкой | |
| 5 | Обведите рамкой слово «да» если утверждение верно и слово «нет», если – неверно | А) Если у человека высокая температура, то он болен. Б) Если человек болен, то у него высокая температура. В) Все звери живут в лесу. Г) Некоторые звери живут в лесу. |
| 6 | Запишите в порядке убывания следующие слова | кило, милли, деци, санти |
| 7 | Найдите два недостающих числа в указанной последовательности | 2; 5; 10; 17;...; 37; 50;...; 82; 101 |
                      8 8
| Установите, какой элемент из II списка соответствует каждому элементу из I списка | I список 1) 2) 3) 4) II список а) б) в) г) |
| 9 | Запишите грамматически правильную последовательность указанных слов | правила очень знает Вася хорошо |
| 10 | Запишите одно слово, которое является общим для всех четырех приведенных слов | хорда медиана высота радиус |
Бланк заданий «теста достижений»
| № | Инструкция | Задание |
| 1 | Вычислите и запишите ответ | а) 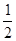 + + 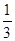 ; б) ; б) 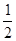 - - 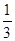 ; в) ; в) 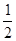 * * 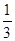 ; г) ; г) 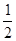 : : 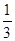
|
| 2 | Вычислите. Правильный ответ обведите рамкой | 7˚ + (-2)3 – 5 · (4,92 – 5,12) – (-1)4 + |-9| |
   3 3
| Установите, какой элемент из II списка соответствует каждому элементу из I списка | I список: 1) углы 6 и 3 2) углы 2 и 3 1 2 а 3) углы 4 и 6 3 4 4) углы 7 и 8 5) углы 5 и 1 5 6 в 7 8 II список а) внутренние односторонние б) внутренние накрест лежащие в) соответственные г) смежные д) вертикальные |
| 4 | Выпишите номера только тех формул, которые являются вернными | 1) а2 + в2 = (а – в) · (а + в) 2) х4 – 16 = (х – 2) · (х + 2) · (х2 + 4) 3) а2 + в2 + с2 = (а + в + с)2 4) с5 – 1 = (с – 1) · (с4 + с3 + с2 + с + 1) |
| 5 | Запишите числа, которые должны стоять на месте пропусков | А) 30% от 120 составляют... Б) 12 составляет 60% от... В) 15 составляет...% от 20 Г) 16 больше, чем 8 на...% |
     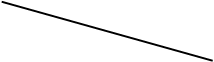  6 6
| Используя приведенный рисунок, найдите длину отрезка А D. Верный ответ обведите рамкой | А | D 150° | В С 12см |
| 7 | Установите, какой элемент из II cписка соответствует каждому элементу из I списка | I список: 1) 2 х = 0; 2) 0 х = 0; 3) 0 х = 2. II список: а) нет корней; б) один корень; в) бесконечно много корней. |
      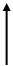 8 8
| Подчеркните ту функцию которой соответствует указанный график | у 1 -1 0 1 х |
                    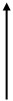 9 9
| Туристы прошли путь из пункта А в пункт F. На графике показана зависимость пройденного ими расстояния (s) от времени (t). Установите, истинно или ложно каждое из приведенных высказываний. Истинные высказывания отметьте знаком «+», а ложные – знаком «-». | А) Протяженность маршрута составила 24 км; Б) Из А в F туристы шли без остановок; В) Участок CD был пройден ровно за 4 ч; Г) Участок AB был пройден со скоростью 8 км/ч S (км) F D 16 В С E 8 1 3 5 7 t (ч) |
| 10 | Катер плывет по реке. Скорость течения реки равна х, а скорость катера в стоячей воде равна у. Какая из формул выражает время, которое затрачивает катер на то, чтобы спуститься вниз по течению на 30 км, а потом сразу вернуться обратно? (Выпишите номер подходящей формулы). | 1) 60 ; у-х 2) 30 + 30 ; у +х у – х 3) 30 + 30; х у 4) 30х + 30у |
|
|
|
|
|
|
Бланк правильных ответов
К «тесту интеллекта»
| № | Ответ к заданию |
| 1 | желтый |
| 2 | Франция, Рим |
    3 3
| Петя выше Оли (Оля ниже Пети) |
               4 4
| 4 8 12 16 24 |
| 5 | А) да / нет; Б) да/ нет; В) да/ нет; Г) да / нет; |
    6 6
| 1) кило; 2) деци; 3) санти; 4) милли |
| 7 | 26 и 65 |
| 8 | 1) – в); 2) – г); 3) – а); 4) – б) |
| 9 | Вася очень хорошо знает правила |
| 10 | Отрезок |
Бланк правильных ответов
К «тесту достижений»
| № | Ответ к заданию |
| 1 | а) 5; б) 1; в) 1 ; г) 3 (или 1 1, или 1,5) 6 6 6 2 2 |
   2 2
| -16; 0; 2; 4; 16 |
  3 3
| 1) – б); 2) - д); 3) - а); 4) - г); 5) - в) |
| 4 | 2) и 4) |
| 5 | А) 36; Б) 20; В) 75; Г) 100 |
    6 6
| 3 см; 4 см; 5 см; 6 см; 9 см |
| 7 | 1) - б); 2) - в); 3) - а) |
| 8 | у = х; у = х2; у = -х; у = |х| |
| 9 | А) +; Б) -; В) -; Г) + |
| 10 | 2) |
РОЛЬ ЗАДАЧ В ОБУЧЕНИИ МАТЕМАТИКЕ.
Важной целью задач является развитие мышления школьников. Задачи служат также основным дидактическим целям: формируют системы знаний, умений и навыков решения различных типов задач, творческое мышление учащихся; способствуют развитию интеллекта, мировоззрения, нравственных качеств, выполняют показательную роль в обучении. Задачи и процессы их решения являются основой реализации целей обучения, воспитания и развития.
Смысл задачи как средства обучения состоит в том, что только с ее помощью учебный материал, подлежит усвоению, может стать «предметом обучения лишь тогда, когда он принимает для учения вид определенной задачи, направляющей и стимулирующей учебную деятельность».
Задачи выступают так же как средство целенаправленного формирования математических способностей, познавательного интереса, самостоятельности, активности учащихся в обучении.
|
|
|
Вопрос о необходимости исследования самих задач как сложных объектов (а не только процессов их решения) в настоящее время четко ставится в психологических, дидактических и методических исследованиях. Так, например, У.Р.Рейтман отмечает: «… если мы попытаемся понять, как люди решают задачи какого-либо вида, нам необходимо иметь хорошее представление о структуре решаемой задачи».
Отсюда становится очевидным то, что эффективность процесса обучения решению задач повысится, если учитель и учащиеся будут иметь ясное представление о структуре задачи. В этом заключается суть задачи как предмета изучения.
Школьная математическая задача, как и любая задача, несет в себе две информации: субъективную и объективную.
Это положение позволило рассматривать задачу как сложный объект, имеющий внешнюю (информационную) и внутреннюю структуру. В связи с этим многие авторы рассматривают задачу как систему (системный подход) (Ю.М.Колягин, В.И.Крупич,Е.И.Машбиц и другие).
С точки зрения информационной структуры задачу можно рассматривать как замкнутую систему S = (A, С, R, D, В), где
А – условия (условие) задачи, то есть данные и отношения между ними;
В – требование задачи, то есть искомые (искомое) и отношения между ними;
С – базис решения задачи, то есть теоретическая и практическая основа, необходимая для обоснования решения;
D – способ, определяющий процесс решения задачи, то есть способ действия по преобразованию условий (условия) задачи для нахождения искомого;
R - основное отношение в системе отношений между данными и искомым.
Информационная структура задачи позволяет различать задачи по степени их психологической сложности (проблемности), как одного из основных компонентов трудности.
Трудность задачи есть психолого-дидактическая категория и представляет совокупность многих субъективных факторов, зависящих от особенностей личности, таких как степень ее новизны, интеллектуальные возможности учащегося, его потребности и интересы, опыт решения задач, уровень владения интеллектуальными и практическими умениями и др. Однако основными компонентами трудности задачи как объекта являются степень ее проблемности и сложности.
|
|
|
Сложность задачи является объективной характеристикой, не зависящей от субъекта. Она определяется внутренней структурой задачи.
Хотя выделен общий механизм построения внутренней структуры следующих задач школьного курса математики (текстовые задачи, дробно-рациональные уравнения, геометрические задачи на вычисление) единого подхода к пониманию внутренней структуры задачи не существует.
Например, А.М.Сохор при выявлении внутренней структуры задачи опирается на характер внутренних отношений (связей, зависимостей) между данными и искомыми величинами.
Е.И.Лященко, Г.Н.Васильева выявляют структуру задачи, исходя из структуры ее решения.
Школьная математическая задача содержит некоторое множество отношений. Например, это отношения между данными, между искомыми, то есть между условием и требованием задачи. В этом множестве отношений на основе обобщения можно выделить главное, ведущее отношение, которое принято называть основным. Основное отношение в общем случае выражает функциональную зависимость между величинами, входящими в условие и требование задачи, и реализовано на предметной области задачи.
Выявление основного отношения в процессе анализа задачи является необходимым условием построения методики обучения решению задач на основе реализации системного типа ориентировки учащихся в этом процессе, а также выявления внутренней структуры задачи, ее элементов.
СИСТЕМНЫЙ ПОДХОД К ОБЪЕКТУ ИССЛЕДОВАНИЯ.
Характерной чертой современной науки является направленность научного познания на управление в природе и обществе. В связи с этим значительное место в научных исследованиях стала занимать общенаучная методология системных исследований.
Обобщенной научной формой ее выражения является системный подход к объекту исследования. Основой этого подхода является философский принцип системности, сущность которого состоит в том, что объект исследования рассматривается как нечто целое, имеющее определенную структуру.
Основными понятиями системного подхода являются система, структура и элемент.
Система – совокупность элементов, находящихся в отношениях и связях между собой и образующих определенную целостность, единство.
Структура – строение и внутренняя форма организации системы, выступающая как единство устойчивых взаимосвязей между ее элементами, а также законов данных взаимосвязей.
|
|
|
Под элементом понимают объект, входящих в состав определенной системы и рассматриваемый в ее пределах как неделимый.
Основными принципами системного подхода являются принцип целостности, принцип сложности и принцип организованности.
Под целостностью понимается такая характеристика объекта, которая позволяет отразить объект в единстве его элементов и связей. Целое выступает как совокупность связей и отношений между его частями, обладающее качественно новыми свойствами.
Целостность объекта проявляется также в сложности и иерархичности строения объекта, в наличии нескольких уровней его организации. Если отсутствует хотя бы один из уровней его организованности, то целостность разрушается.
Иерархичность системы означает, что каждая ее подсистема может рассматриваться как система, а сама исследуемая система представляет собой лишь одну из подсистем более широкой системы (количество элементов, связей и др.).
Отметим, что деятельностный подход к процессу обучения при исследовании объекта также опирается на принципы системного подхода.
Действительно, если рассмотреть структуру человеческой деятельности, состоящую из следующих взаимопереходящих друг в друга элементов: деятельность, действие, операция и потребность, мотив, цель; с точки зрения системного подхода, то здесь действуют все основные принципы системного подхода: целостность, сложность и иерархичность (организованность).
Основные принципы системного подхода находят непосредственную реализацию в процессе анализа объективной информации, определяющей внутреннюю структуру и сложность задачи.
Глава 2. Методические основы уровневой дифференциации.
В данной главе мы более подробно рассмотрим такие способы организации учебной деятельности в условиях дифференцированного обучения как фронтальная, групповая и индивидуальная работа, и их практическую реализацию. Глава содержит также ряд практических задач различной степени сложности.
Формирование математического мышления предполагает целенаправленное развитие на предмете математики всех качеств, присущих естественнонаучному мышлению, комплекса мыслительных умений в органическом единстве с формами проявления мышления.
В процессе обучения математике, естественно уделять особое внимание развитию у учащихся качеств мышления, специфичных для мышления математического. Органическое сочетание и повышенная активность разнообразных компонентов мышления вообще и различных его качеств проявляются в особых способностях человека, дающих ему возможность успешно осуществлять деятельность творческого характера в разнообразных областях науки. Математические способности – это определенная совокупность некоторых качеств творческой личности, сформированных и применяемых в процессе математической деятельности.
Совокупность способностей, присущих творческой личности, реализуемых в процессе мышления, называют творческим мышлением.
Факторы творческого развития выражаются в следующих принципах:
1) творческие потенциалы заложены в каждом ребенке;
2) развитие творческого стиля мышления происходит только в творческой деятельности;
3) формирование творческой инициативности зависит от условий социальной среды.
Итак, можно сделать следующий вывод: творчество – природная функция мозга, творчество зависит от условий обучения.
Создание этих условий одно из важнейших задач педагога. Одним из них является выбор формы организации работы и типа урока по технологии - творческого развития.
1-ый тип урока – урок анализа домашнего задания
2-ой тип урока – урок выравнивания знаний.
Цель урока - Создать для всех учащихся равные стартовые условия до начала изучения нового учебного материала, т.е. выравнивание знаний по усвоенному ранее материалу.
3-ий тип урока – урок постановки учебной задачи.
Цель урока – научить учащихся целеобразованию, формулировать учебные задачи на первом этапе урока.
При традиционном обучении учебные цели ставит сам учитель, а учащиеся должны их принять к исполнению. Технология урока творческого развития предполагает создание ситуации целеобразования, где возникает процесс порождения новых целей в учебной деятельности, что является одним из важных проявлений творческого мышления.
Целеобразование может быть непроизвольным и произвольным, когда цель возникает в результате специального намерения и планирования.
Существуют различные механизмы целеобразования:
1) внешние требования учителя превращаются в индивидуальную цель;
2) превращение мотивов в цели при их осознании;
3)преобразование неосознанных предвидений в цели и т.д.
4-й тип урока – урок решения учебной задачи (УЗ).
Цель урока – Научить учащихся теоретическому анализу учебного материала, развивать и формировать диалектико-логический, творческий способ мышления.
Процесс решения учебной задачи самый ответственный этап урока, где формируются интеллектуальные способности, творческое мышление, способность к самодвижению
Учебная задача только тогда является действительно «учебной», если она квалифицированно расчленена на дискретные части, т.е. на элементарные задания, раскрывающие УЗ только с какой-то одной стороны. При этом каждое задание у учащихся вызывает проблемную ситуацию.
Максимальные результаты в обучении и воспитании учащихся возможны только при комплексном и умелом использовании всех научных открытий и рекомендаций. Однако для этого нужен совершенно другой тип специалистов, работающих на уровне педагогической акмеологии, т.е. ученые и учителя, достигшие высшей степени профессионализма. К сожалению, фактическое положение таково, что одни знают, что такое развивающее обучение, другие – что такое проблемное обучение, третьи – еще что-то, но трудно найти специалистов, которые в равной мере умели бы продуктивно использовать результаты разных научных школ.
5-й тип урока – урок формирования общего способа.
Цель урока – научить учащихся выделению учебных (умственных) действий и формулировать на их основе общие способы в процессе решения учебной задачи.
6-й тип урока – урок моделирования содержания материала или способов решения.
Цель урока – научить учащихся действиям моделирования усвоенного учебного материала в графической, знаковой, символической или другой форме.
Учебное моделирование – это процесс чистого творчества, великолепное средство познания и содержательного обобщения знаний и способов действий. Учебная модель является результатом творческого анализа научного понятия и условием формирования устойчивой мотивации учения.
Урок моделирования может проходить в двух формах: как процесс (фиксированный в наглядно-логической форме), как результативное средство (модель фиксирования в конце урока в результате специального задания).
7-й тип урока – урок самоконтроля.
Цель урока – научить учащихся осуществлять контроль над своими учебными действиями.
Самоконтроль – основное нравственное действие человека связанное с развитостью его волевой сферы. Самоконтроль осуществляется на основе личностно значимых мотивов и установок, что ведет к рациональной рефлексии и оценке учащимися своих собственных учебных действий. Самоконтроль учащихся предполагает сличение, анализ и коррекцию отношений между целями, средствами и результатами.
Различают следующие основные виды:
1) итоговый контроль (по результату);
2) процессуальный;
3) прогнозирующий;
8-й тип урока – урок самооценки.
Цель урока - научить учащихся осознавать степень усвоения учебного материала и адекватно оценивать свои знания.
Школьная самооценка - это оценка учеником самого себя, своих знаний, возможностей, качеств и занимаемого места среди одноклассников. Учебная самооценка является важным регулятором поведения школьника и относится к главному фактору формирования личности.
В самооценке необходимо выделять ее адекватность, надежность и полноту.
9-й тип урока – урок учебной деятельности (творческого развития).
Цель урока - научить детей работать в ситуации целостной учебной деятельности, где в свернутой, обобщенной, сокращенной форме одновременно присутствуют все типы уроков как структурные, естественные компоненты типичного (обычного) урока творческого развития.
Обычный, «классический» тип урока творческого развития в себя включает все «чистые типы» уроков.
10-й тип урока – урок усвоения групповых форм учебной деятельности.
Цель урока - научить учащихся работать в группах, знания добывать совместными усилиями.
2.1. Фронтальная работа.
Фронтальная работа может осуществляться в нескольких видах:
- подача нового материала;
- устные упражнения – как средство для повторения и моделирования проблемы;
- работа с классом.
Значение этого метода достаточно велико, но для повышения эффективности обучения необходимо комбинировать его с другими формами.
Задания для фронтальной работы могут быть направлены на активизацию
1) процесса памяти;
2) процесса логического мышления на базе имеющихся навыков и знаний;
3) творческой деятельности и поиска новых знаний.
Рассмотрим несколько примеров реализации дифференцированного подхода во фронтальной работе
Пример 1. Для примера выберем тему «Прогрессии»
Покажем план урока подачи нового материала в классах различного типа и уровня развития.
1. Класс сильный, думающий, увлеченный математикой.
Сама математика как предмет держат его внимание. Потому, с одной стороны, в таком классе легко работать, но с другой стороны, есть и сложности. Особенно если тема простая, а рассматриваемая нами тема «Прогрессии» не содержит сложного материала.
Если идти по пути построения урока, достойного развития детей, то можно начать изучение двух тем параллельно. Например, дается определение арифметической прогрессии, приводятся примеры, и тут же рядом записывается определение геометрической прогрессии, составленное по аналогии самими учащимися. Действительно, если есть арифметическая прогрессия, то, наверное, существует и геометрическая.
Затем встает вопрос о формуле любого числа. Здесь сами ребята догадаются о ее структуре и докажут справедливость. Учителю придется подсказать лишь каким методом это сделать. Уместен будет разговор о методе математической индукции, хотя в качестве информации.
Последними можно рассмотреть характеристические свойства.
При всем этом нельзя забывать, что даже этот круг учеников нуждается в отработке элементарных операций. Поэтому далее целесообразно включить устную работу (10-15 мин.), направленную на отработку специальных умений по этой теме. Затем решить по одной задаче на характеристическое свойство каждой из прогрессий.
Закончить урок можно решением таких задач:
Задача 1. Выписаны 2 арифметические прогрессии. Если из каждого члена первой прогрессии вычесть соответственно член второй прогрессии, то получится ли снова арифметическая прогрессия?
Решение:
Ответ: да.
Задача 2. Могут ли три последовательных члена арифметической прогрессии вместе с тем быть и тремя последовательными членами геометрической прогрессии? (прогрессии с неравными членами).
Решение: Пусть числа а, в, с, образуют арифметическую прогрессию и геометрическую одновременно, тогда:
Ответ: нет.
Задача 3. В двух трехчленных прогрессиях (арифметической и геометрической с положительными членами) одинаковы оба первых и оба последних члена. В какой из них сумма членов больше?
Ответ:в арифметической.
Однако вместо этих задач можно сделать экскурс в историю. Рассказать о том, что примеры отдельных арифметических и геометрических прогрессий можно встретить еще в древне-вавилонских и египетских надписях (500-400 лет до нашей эры), что в Древней Греции были известны такие суммы:
А знаменитая задача о награде за изобретение шахматы впервые встречается у хорезмского математика Аль-Бируни
Можно упомянуть и о бесконечных рядах и их применении. Впечатляет и способ вычисления суммы бесконечного ряда
2. Класс шумный, думающий, заинтересованный предметом, но с недостаточно развитой самостоятельностью действий.
В этом случае работа будет носить фронтально-индивидуальный характер. Учащиеся, отвечающие вышеизложенной характеристике, любят учиться, но испытывают тягу к получению быстрых результатов. Однако с большим интересом воспринимают информацию о самих себе: о своей памяти, внимании, работоспособности. Учитель должен завладеть вниманием учащихся и удержать его до конца урока. Класс с готовностью выполняет четкие указания учителя и этот момент надо непременно использовать. Но необходимо не трафаретное начало. Поэтому учащихся можно сразу озадачить вопросами: какие анализаторы человек использует при восприятии информации? Дальше можно сказать, что основными являются анализаторы запаха, вкуса, осязания, слуха. Для рационального восприятия необходимо знать свой доминирующий анализатор, обычно зрение или слух. Именно его следует использовать в первую очередь. Для выявления учеников предлагаются задания следующего типа. На доске записаны числа 6,8,10,12,14,16,18,20;-12; -9; -6; -3; 0; 3; 6; 9; 12.
Учащиеся после минутного рассмотрения должны воспроизвести запись в тетрадях, что удается не каждому. Далее им предлагается ряд равенств, для запоминания которых включается не только зрительная, но и логическая память:
Затем делается акцент на слуховую память: медленно читается определение, которое необходимо записать после прослушивания.
«Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называется арифметической прогрессией». После паузы читается определение еще раз и все проверяют запись.
После этого можно сделать общий вывод принципов рационального восприятия информации:
1. Постановка цели: что люди мыслят под этим понятием, хочу про него знать все.
2. Использование основного анализатора.
3. Интерес.
Далее дети читают в своем темпе параграф по теме.
Завершает урок ряд задач из учебника или подобранных учителем.
Пример 2. Устные упражнения.
Устные упражнения заслуживают особого внимания. Они эффективны кажущейся легкостью, эмоциональностью, действуют на учащихся мобилизующе, способствуют развитию внимания и памяти, но требуют от школьников большого умственного напряжения, поэтому могут быстро их утомить.
На ряду с чисто устными практикуются также полуустные (зрительно-слуховые), когда задания записаны на доске или проецируется на экран. Некоторые мы рассматривали в предыдущем примере, когда с их помощью вводился новый материал.
Устные упражнения успешно применяются и при повторении. Например, при подготовке к контрольной работе в 8 классе по теме «арифметический квадратный корень» можно предложить следующую систему устных упражнений:
- в начале урока:
1) Известно, что площадь квадрата составляет а2; 36; 900 кв.ед. Чему равна его сторона?
Запись на доске:
2) Сравнить значения выражений:
3) Упростить выражения:
4) Назвать область определения:
5) Решить уравнения (назвать его корни):
- после блока повторения – построение графиков:
1) указать ход построение графиков:
Приведем так же пример обобщающего повторения. В начале 9 класса необходимо восстановить в памяти учащихся все о квадратном трехчлене и квадратных уравнениях с помощью упражнений:
1. Указать общий вид квадратных уравнений, корни которых равны по величине, но противоположны по знаку:
2. При каком значении «а» один из корней уравнения
3. Выразите зависимость между коэффициентами уравнения
4. Составьте такое уравнение, чтобы сразу было видно, что оно имеет три корня 0; 2; 5.(Ответ:
Фронтальную работу можно использовать так же при текущем контроле знаний и умений учащихся. Например, в форме математического диктанта, при чем задания можно давать повариантно: первый вариант доказывает свойство умножения степеней с одинаковыми основаниями, второй – свойство возведения степени в степень; в качестве второго задания даются не сложные примеры на вычисление и т.п.
2.2 Групповая работа.
Для того, чтобы обучение проявляло развивающий эффект, необходимо соблюдать универсальное условие: развиваемый субъект должен быть включен в активную деятельность и общение. Это условие вытекает из того, что ученик в учебном процессе не только объект, но и субъект процесса собственного учения.
Формирование творческой активности – высшая цель активизации, но нельзя игнорировать более низкие ее ступени. К содержательной стороне активизации относятся составление и предъявление заданий, активизирующих учебно-познавательный процесс. Другой ее стороной является организация активизированной учебной работы.
Групповая работа – одна из форм активизации учащихся. По определению Х.И.Лийметса под групповой работой понимают такое построение работы, при которой класс делится на группы по 3-8 человек (чаще по четыре человека) с целью выполнения той или иной учебной задачи.
Групповая работа так же представляет много возможностей для индивидуализации, особенно, если группы составлены из схожих по какому-либо признаку учащихся, причем тогда для каждой группы подбираются специальные задания.
В малой группе учащийся находится в более благоприятных условиях, чем при фронтальной работе. Группы могут быть сформированы как учителем (на основании уровня знаний и/или умственных способностей), так и по пожеланию учащихся.
Групповая работа достаточно эффективна, однако следует следить за тем, чтобы более сильные и старательные не заглушали инициативу более слабых и пассивных. Целесообразно проводить работу также с относительно стабильными группами, что позволяет оперативно распределять задания различной степени сложности, причем по результатам обучения возможен переход из одной группы в другую.
И так групповая учебная деятельность – это организованная система активности взаимодействующих учащихся, направленная на целенаправленное р
|
|
|


