Задачи для самостоятельного решения

Задача 1. Используя "Поиск решения" найти экстремум функции

f(x)=x ⁴ – 3 x

Сохранить результат в виде сценария. Произвольно задать два других значения аргумента, сохранить результаты в виде сценариев. Создать отчет по сценариям.

Задача 2. Найти x и y, при которых достигается наименьшее значение функции:

f (x,y)=–2 x –6 y + x ²–2 xy +2 y ²

при ограничениях: x ³0, y ³0, x + y £2, 2 y – x £2.

Задача 3. Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1т карамели данного вида приведены в таблице. В ней также указано общее количество сырья каждого вида, которое может быть использовано фабрикой, и прибыль от реализации 1т карамели данного вида. Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации.

Вид сырья	А	В	С	Общее кол-во сырья
Сахарный песок	0,8	0,5	0,6
Патока	0,4	0,4	0,3
Фруктовое пюре	-	0,1	0,1
Прибыль от реализации 1т продукции

Задача 4. Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В – 4 м². фирма может получать от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В – 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 долл. прибыли, а каждое изделие модели В – 4 долл. прибыли?

Задача 5. При получении школой нового компьютерного класса необходимо оптимально спланировать использование единственного легкового автомобиля для перевозки 15 компьютеров. Каждый компьютер упакован в две коробки (монитор и системный блок) и существуют три варианта погрузки коробок в автомобиль.

Способы погрузки

Тип коробки	Варианты погрузки
Мониторы
Системный блок

Необходимо выбрать оптимальное сочетание вариантов погрузки для того, чтобы перевезти 15 коробок с мониторами и 15 коробок с системными блоками за минимальное количество рейсов автомобиля.

Задача 6. Имеются три сплава. Первый сплав содержит 70% олова и 30% свинца, второй – 80% олова и 20 % цинка, третий – 50% олова, 10% свинца и 40% цинка. Из них необходимо изготовить новый сплав, содержащий 15% свинца. Какое наибольшее и наименьшее процентное содержание олова может быть в этом сплаве?

Задача 7. Фирма производит три вида продукции А, В, С, для выпуска каждого требуется определенное время обработки на всех четырех устройствах I, II, III, IV

Вид продукции	Время обработки, ч	Прибыль, долл
I	II	III	IV
А
В
С

 

Пусть время работы на устройствах соответственно 84, 42, 21, 42 часа. Определите, какую продукцию и в каких количествах стоит производить для максимизации прибыли (рынок сбыта для каждого продукта не ограничен).

Задача 8. Имеются 6 предметов, каждый из которых характеризуется весом и ценой:

Предмет	вес	цена

Нужно выбрать из них такие предметы, чтобы их общий вес не превышал 12, а суммарная цена была максимальной.

Задача 9. Транспортная задача

Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i – гопункта производства в j– й центр распределения с_ij приведена в таблице, где под строкой понимается пункт производства, а под столбцом – пункт распределения. Кроме того, в этой таблице в i – й строке указан объем производства в i – м пункте производства, а в j– м столбце указан спрос в j– м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.

Вариант 1.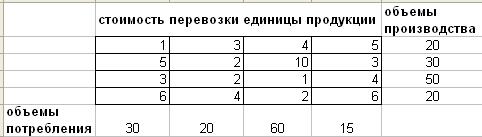

Вариант 2.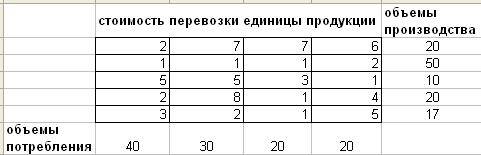

Задача 10. Задача о назначениях

Имеются n рабочих и m видов работ. Стоимость c_ij выполнения i- м рабочим j- й работы приведена в таблице, где рабочему соответствует строка, а работе– столбец. необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была бы минимальной.

Вариант 1.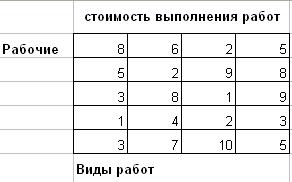

Вариант 2.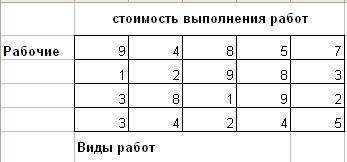

Задача 11. Линейная оптимизационная задача

Вариант 1. Фирма имеет возможность рекламировать свою продукцию, используя местные радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой $1 000 в месяц. Каждая минута радиорекламы обходится в $5, а каждая минута телерекламы – в $100. фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше объема сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Вариант 2. Фирма производит два вида продукции – А и В. Объем сбыта продукции А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции и В равны 20 и 40 долларов, соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Задача 12. Система нелинейных уравнений. Найти все решения системы нелинейных уравнений.

Вариант 1.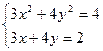

Вариант 2.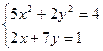

Вариант 3.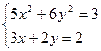

Списки

Список - определенным образом сформированный на рабочем листе Excel массив данных со столбцами и строками.

Первая строка списка при этом содержит названия полей (столбцов). Строки выступают в качестве записей, а столбцы являются полями.

Фильтрация данных позволяет выбрать из списка только те записи, которые удовлетворяют некоторому условию

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: