 |
Предварительный анализ проблемы
|
|
|
|
На этом этапе определяются:
- главные цели;
- уровни рассмотрения, элементы и структура процесса;
- подсистемы и используемые ими основные ресурсы, критерии качества функционирования подсистем;
- основные противоречия, узкие места и ограничения.
Основная задача этого этапа заключается в определении целей, которых необходимо достичь в процессе управления. Непосредственное участие в процессе формирования этих целей должен принимать руководитель.
Цели должны быть конкретными и выражаться измеримыми значениями, чем задаются показатели, которые будут использоваться в дальнейшем для выбора варианта управленческого решения и контроля по реализации управляющих воздействий.
Под воздействием внутренних или внешних факторов или при получении дополнительной информации цели могут изменяться во времени. Таким образом, при формулировке целей управления важно учитывать как факторы взаимодействия (внутренние и внешние), так и временной фактор.
Для определения уровней рассмотрения, элементов и структуры процесса может быть использован, в частности, подход, предусматривающий декомпозицию главной цели до того уровня детализации, когда для нижнего уровня иерархии целей можно сформулировать критерии, позволяющие адекватно описать степень достижения при принятии той или иной альтернативы (рис. 3).
Так, главная цель фирмы – выбор варианта внедрения СППР с целью повышения рентабельности фирмы.
Критериями оценки вариантов могут выступать, например, затраты на внедрение, способность поддерживать решения, возможность адаптации к другим видам деятельности фирмы, возможность защиты информации, время реакции на запрос, надежность оборудования и пр. Наборы значений этих критериев используются для описания исходов альтернативных вариантов решений (в дальнейшем − «альтернатив»). Для решения таких сложных проблем следует привлекать многих специалистов из разных областей знания, что при использовании такого подхода весьма затруднительно.
|
|
|
Цели управления должны учитывать всю накопленную объективную и субъективную информацию, а также согласовываться с имеющимися возможностями и ресурсами. В качестве технологий на этом этапе могут использоваться методики SWOT-анализа (strengths and weaknesses, opportunities and threats − достоинства и недостатки, возможности и
угрозы), сегментного анализа и т. д.
Рис. 3. Декомпозиция целей
Если поставленные цели не согласуются с имеющимися ресурсами и возможностями, то они могут оказаться недостижимыми. Это может выявиться на последующих этапах процесса поддержки принятия решения, что приведет к возврату на первый этап для уточнения и корректировки ранее поставленных целей и показателей.
Постановка задачи
Постановка конкретной задачи принятия решений (ЗПР) включает:
- формулировку задачи;
- определение типа задачи;
- выбор метода решения;
- определение множества альтернатив и основных критериев для выбора из них наилучшей и согласование критериев.
Для решения задач широко применяются различные методы.
3.2.1. Математическое моделирование при принятии решений
При построении, изучении и применении экономико-математических моделей принятия решений используются различные математические методы, именуемые экономико-математическими. Их можно разделить на несколько групп:
- методы оптимизации;
- методы, учитывающие неопределенность, прежде всего вероятностно-статистические;
- методы построения и анализа имитационных моделей;
- методы анализа конфликтных ситуаций (теории игр).
Во всех этих группах можно выделить статическую и динамическую постановки. При наличии фактора времени используют дифференциальные уравнения и разностные методы.
|
|
|
Математическое программирование – это семейство инструментальных средств, созданных для помощи в процессе решения управленческих задач, при котором лицо, принимающее решения, должно выделить ограниченные ресурсы для различных действий или операций с условием оптимизации измеримой цели. Наиболее известным методом этого семейства инструментов является линейное программирование. Оно широко используется в информационных системах поддержки руководителя (ИСПР) и имеет много важных практических приложений, например решение задачи распределения (ресурсов или времени).
Задачи распределения, решаемые на основе линейного программирования, обычно отражают следующие характеристики:
- для распределения доступно ограниченное количество ресурсов;
- ресурсы используются в производстве продукции или услуг;
- существует два или более путей использования ресурсов, каждый из которых называется решением или программой;
- распределение обычно ограничивается несколькими доступными пределами и требованиями, называемыми ограничениями.
Модель распределения линейного программирования основывается на следующих различных экономических допущениях:
- отдача или доходность при различных вариантах распределения могут сравниваться, т.е. они могут быть измерены в общих единицах
(например, денежных);
- отдача от одного распределения независима от других распределений;
- общая доходность является суммой доходностей, принесенных различными действиями;
- все исходные данные известны и определены.
Наиболее известны задачи линейного программирования, в которых максимизируемая функция F(X) является линейной, а ограничения А задаются линейными неравенствами.
Пример [4]. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола – 20 (футов красного дерева). Трудоемкость изготовления одного стула 10 человеко-часов, стола – 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула – 45 долларов США, при производстве стола −
80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?
|
|
|
Введем обозначения: Х1 – число изготовленных стульев;
Х2 – число сделанных столов. Задача оптимизации имеет вид:
45 Х1 + 80 Х2 → max;
5 Х1 + 20 Х2 ≤ 400;
10 Х1 + 15 Х2 ≤ 450;
Х1 ≥ 0;
Х2 ≥ 0.
В первой строке выписана целевая функция − прибыль при выпуске Х1 стульев и Х2 столов. Ее требуется максимизировать, выбирая оптимальные значения переменных Х1 и Х2. При этом должны быть выполнены ограничения по материалу (вторая строчка) − может быть истрачено не более 400 футов красного дерева, а также и ограничения по труду (третья строчка) − работы выполнялись в течение 450 часов. Кроме того, нельзя забывать, что числа столов и стульев положительны.
В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
Условия производственной задачи можно изобразить на координатной плоскости. По горизонтальной оси абсцисс будем откладывать значения Х1, а по вертикальной оси ординат − значения Х2.
 | |||
|
Таким образом, множество возможных значений объемов выпуска стульев и столов (Х1, Х2) представляет собой выпуклый четырехугольник, показанный на рисунке 4. Три его вершины очевидны − это (0,0), (45,0) и (0,20). Четвертая − это пересечение двух прямых, т. е. решение системы уравнений следующее:
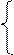5Х1 + 20Х2 = 400;
10Х1 + 15Х2 = 450.
Из первого уравнения: 5Х1 = 400 − 20Х2; Х1 = 80 − 4Х2. Подставляем во второе уравнение: 10(80 − 4Х2) + 15Х2 = 800 − 40Х2 + 15Х2 =
= 800 − 25Х2 = 450, следовательно, 25Х2 = 350, Х2 = 14. Отсюда
Х1 = 80 − 4×14 = 80 − 56 = 24. Итак, четвертая вершина четырехугольника − это (24, 14).
Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. Максимум целевой функции, равный 2200, достигается в вершине (24, 14).
Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.
|
|
|
