 |
Взаимное положение точки и прямой
|
|
|
|
Точка принадлежит прямой, если проекции точки расположены на одной линии связи и на соответствующих проекциях прямой.
 |
Рис. 12
Точки А и В (рис. 12) принадлежат прямой f. А2, В2 и А1, В1 лежат соответственно на f2 и f1 и между собой на линиях связи.
Точки C и D по той же причине не принадлежат прямой f (обе проекции точки D не принадлежат одноименным проекциям прямой f, горизонтальная проекция C1 не принадлежит горизонтальной проекции f1).
Расстояние измеряется между точками. Следовательно, если прямую АВ расположить, например, перпендикулярно П1, то горизонтальная проекция будет точка А21=В21. Расстояние от точки D до АВ будет равно D21 А21.
Горизонтальная проекция прямой А1В1 и горизонтальные проекции точек D1 и С1 повернуты вокруг оси ZA до положения, в котором YA = YB, угол bАВ = 0 и перенесены в положение А11В11, D11, С11.
Чтобы сохранить геометрические размеры горизонтальной проекции
Объекта (прямая и 2 точки) в текущем положении 1, в исходном положении из горизонтальных проекций точек C1 и D1 опустим перпендикуляры C1К и D1Н на горизонтальную проекцию прямой А1В1. Для построения в первом текущем положении горизонтальной проекции точки С11 от горизонтальной проекции точки А11 отложено расстояние (А11 К) = (А1 К), из точки К восставлен
перпендикуляр (КС11) = (КС1). Для построения горизонтальной проекции
точки D11 от горизонтальной проекции точки А11 отложено расстояние (А11Н)=(А1Н), из точки Н восставлен перпендикуляр (НD11)=(Н D1).
Фронтальные проекции точек А12, В12, С12 и D12 расположены на пересечении линий связи к оси Х через точки А11, В11, С11 и D11 и линий связи к оси Z через точки А2, В2, С2 и D2.
На П2 измерим угол aАВ и повернем фронтальную проекцию в положении один на угол 90° - aАВ вокруг оси YA1. Перенесем в положение 2.. Положение фронтальной проекции точки D22 определено расстояниями от концов фронтальной проекции отрезка (А22 В22) и находится на пересечении дуг радиусами R=(А12 D12) и R=(В12 D12). Аналогично построена фронтальная проекция точки С22.
|
|
|
Взаимное положение прямых
Параллельные прямые имеют одинаковые углы наклона к плоскостям проекций, но расстояние между ними не равно 0 (базовая точка одной прямой не принадлежит другой прямой). На рис. 13 прямая a(a 1, a 2)и параллельная ей прямая е(е1, е2) заданы проекциями на плоскости П1 и П2.
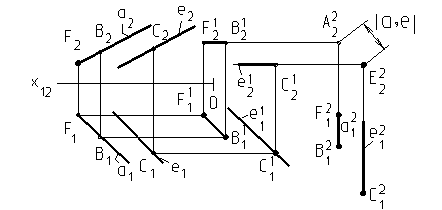
Если прямые параллельны, то параллельны их одноименные проекции (a1 ½½ е1) и (a2 ½½ е2). Для параллельных прямых следует определить расстояние между ними.
Рис. 13

Пересекающиеся прямые имеют общую точку А, проекции которой лежат на одной линии связи к оси Х и совпадают с точками пересечения одноименных проекций, угол между прямыми j больше 0 (рис. 14).
Рис. 14
Скрещивающиеся прямые - не пересекаются (расстояние между ними не равно 0), не параллельны (угол между ними не равен 0). На плоском чертеже точки пересечения одноименных проекций не лежат на одной линии связи к оси Х (рис. 15).
При определении расстояния и угла между прямыми следует исходить из условия, что через две скрещивающиеся прямые можно всегда провести две параллельные плоскости.
Плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся
прямым другой плоскости.
Через точку А проведем прямую АЕ, которая параллельна прямой СD.
В результате получим треугольник АВЕ, который параллелен прямой CD.
Прямая параллельна плоскости, если она параллельна прямой,
которая принадлежит плоскости.
В плоскости АВЕ возьмем прямую АР, угол b AР = 0. Измерим угол aАЕ между А2Р2 и А1Р1, повернем фронтальные проекции С2D2, А2В2Е2 вокруг оси YA на угол 90° - aАЕ и перенесем в положение C12D12, А12В12Е12.
|
|
|
Горизонтальная проекция треугольника А11В11Е11 – прямая, с ней совпадет горизонтальный след плоскости D11. Горизонтальная проекция прямой C11D11 , которая будет параллельна А11В11Е11. С C11D11 совпадет горизонтальный след S11 плоскости, проходящей через CD и параллельной АВЕ.
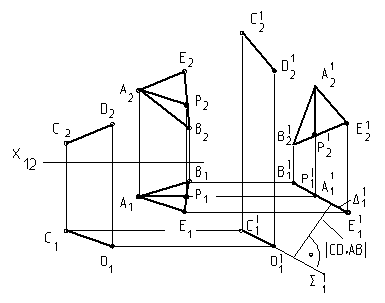 |
Рис. 15
Расстояние между плоскостями ½D11 S11½ равно расстоянию между прямыми ½CD, AB½.
Угол между прямыми CD Ù AB равен углу между сторонами треугольника АВ Ù АЕ. Измерять угол следует в натуральной величине треугольника.
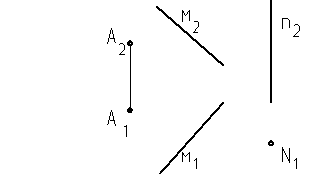 |
Домашняя работа: Через точку А провести прямую АК, которая пересекает прямые м и n.
|
|
|


