 |
Взаимное положение прямой и плоскости
|
|
|
|
 Прямая принадлежит плоскости:
Прямая принадлежит плоскости:
- имеет 2 общие точки с плоскостью (в плоскости пересекает 2 прямые);
- имеет 1 общую точку с плоскостью и параллельна некоторой прямой, которая принадлежит плоскости.
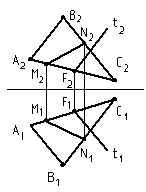
На рис. 16 прямая МN принадлежит плоскости треугольника АВС. Точки М и N лежат на соответственно на АС и ВС.
Прямая t принадлежит плоскости АВС, так как точка F лежит на прямой АС и прямая t параллельна стороне треугольника АВ (t2 парал-
Рис. 16 лельна А2В2, t1 параллельна А1В1).
Прямая не принадлежит плоскости:
t параллельна плоскости, если она параллельна
прямой d, которая принадлежит плоскости,
t пересекает плоскость, то она пересекает
прямую d, которая принадлежит плоскости.
 |
На рис. 17а прямая t пересекает плоскость АВС в точке К, так как в
Рис. 17
этой точке прямая t пересекает прямую d, которая принадлежит плоскости.
Прямая d принадлежит плоскости, так как точки M и N принадлежат сторонам треугольника.
На рис. 17б прямая t параллельна плоскости так как t параллельна прямой d, которая принадлежит плоскости (d имеет с плоскостью общие точки M и N).
Примечание:
Прямую d, по отношению к которой определяется положение к плоскости прямой t, следует выбирать из условия, что d и t лежат в одной плоскости. В противном случае они не могут пересекаться.
Однозначно прямые лежат в одной плоскости, если:
1. Совпадают их фронтальные проекции (d2 совпадает с t 2). Прямые лежат в плоскости, которая перпендикулярна П2.
2. Совпадают их горизонтальные проекции (d1 совпадает с t 1). Прямые лежат в плоскости, которая перпендикулярна П1.
Взаимно перпендикулярные прямые
Две прямые взаимно перпендикулярны, если одна из них
|
|
|
принадлежит плоскости, перпендикулярной второй прямой
Прямая перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся прямым
в этой плоскости.
 На рис. 18 построена прямая ЕК, которая перпендикулярна прямой a и пересекает ее в точке К:
На рис. 18 построена прямая ЕК, которая перпендикулярна прямой a и пересекает ее в точке К:
- взяли произвольную точку Е;
- через точку Е построили плоскость S(h Ç f), заданную двумя пересекающимися прямыми; прямая h перпендикулярна прямой a (угол наклона прямой h к П1 a=0 и горизонтальная проекция h1 ^ a1), прямая f тоже перпенди-кулярна прямой a (угол наклона прямой f к П2 b=0 и фронтальная проекция f 2 ^ a2);
- определена точка К – пересечение прямой a с плоскостью S (в плоскости S взяли прямую d, фронтальная проекция которой d2 совпадает с фронтальной проекцией a2 прямой a; прямая d проходит через точку 1(11, 12), принадлежащую
Рис. 18 прямой f, и точку 2(21,22), принадлежащую прямой
h; горизонтальная проекция точки К1 – на пересечении горизонтальных проекций a1 и d1, фронтальная проекция - на линии связи к оси Х и на a2). Прямая ЕК перпендикулярна прямой a, т.к. ЕК лежит в плоскости S, перпендикулярной прямой a.
Через точку К в плоскости S можно построить веер прямых, которые будут перпендикулярны a.
На рис. 19 построена прямая MN, которая скрещивается с прямой g и перпендикулярна ей. С этой целью на прямой g взяли точку D и построили плоскость D, которая задана пересекающимися в точке D прямыми h и f.
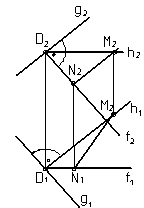
Обе прямые перпендикулярны прямой g
(ah = 0, h 1 ^ g1; bf = 0, f 2 ^ g2).
Если прямая принадлежит плоскости D и не проходит через точку D, то по отношению к прямой
g она будет скрещивающейся. У прямой MN фронтальная проекция M2N2 параллельна g2, а горизонтальная проекция M1N1 при продолжении пересекает g1, следовательно, прямые MN и g скрещиваются.
Любая прямая, которая расположена в плоскости D будет перпендикулярна прямой g.
При этом прямые, пересекающие прямую g,
Рис. 19 будут проходить через точку D.
|
|
|
|
|
|


