Разработка имитационной модели

Министерство образования РФ

Пермский национальный исследовательский политехнический университет

Кафедра «Автоматика и телемеханика»

 

Прикладная теория систем массового обслуживания

КУРСОВАЯ РАБОТА

Вариант № 3.2.8

 

Выполнил:	студент гр. ТКбз-10 Арапов Р.А. Дата ________________ Подпись _____________
Проверил:	Профессор кафедры АТ Южаков А.А. Дата ________________ Подпись _____________

 

 

Пермь 2013

Содержание

Введение
1 Техническое задание
2 Описание системы
3 Разработка имитационной модели
	3.1 Математическое описание имитационной модели
	3.2 Описание блок-схемы алгоритма
	3.3 Анализ полученных результатов имитационного моделирования
4 Разработка аналитической модели
	4.1 Математическое описание аналитической модели
	4.2 Расчет параметров СМО
	4.3 Анализ полученных результатов аналитического моделирования
5 Сопоставление полученных результатов для разработанных моделей
Заключение
Список используемой литературы
Приложения
	Приложение 1 Листинг программы имитационного моделирования
	Приложение 2 Листинг программы аналитического моделирования
	Приложение 3 Таблицы результатов моделирования
	Приложение 4 Графики, полученные в результате моделирования

 

Введение

Теория систем массового обслуживания является одной из наиболее развивающейся ветвей теории вероятностей, т.е. опирается на ее аппарат, но является самостоятельной наукой. Трудно даже перечислить все области практики, где находят применение методы теории системы массового обслуживания (СМО). Область применения математических методов теории СМО непрерывно расширяется и выходит за пределы задач, связанных на прямую с «обслуживающими организациями» в буквальном смысле слова. Многие задачи автоматизации производства оказываются близкими к теории массового обслуживания: потоки деталей, поступающих для выполнения над ними различных операций, могут рассматриваться как потоки заявок, ритмичность поступления которых нарушается за счет случайных причин.

Проблемы, родственные задачам массового обслуживания постоянно возникают в военном деле. Каналы наведения, линии связи, аэродромы, устройства сбора и обработки информации представляют собой своеобразные СМО. Системы массового обслуживания настолько велики и разнообразны, что описать их все не представляется возможным.

В данной работе рассматривается работа системы противовоздушной обороны с точки зрения теории массового обслуживания.

Целью моделирования – аналитического и имитационного – является прогноз производительности системы путем оценки характеристики использования ресурсов. Моделирование представляет исследуемый объект как систему массового обслуживания, узлами которой служат противовоздушные установки и навигационное оборудование, а заявками – самолеты противника. Модели приближенно отражают структуру и алгоритм функционирования объекта. Во многих случаях теория СМО обеспечивает подходящий компромисс между требованиями к точности модели, сложностью получения численных результатов и возможностью их интерпретации.

 

Техническое задание

Ознакомиться и промоделировать работу системы ПРО с отказами и частичной взаимопомощью между каналами со следующими характеристиками:

 

· Дисциплина обслуживания		система с отказами и частичной взаимопомощью
· Скорострельность каждой пусковой установки (выстрелов в минуту)
· Вероятность поражения цели одной ракетой
· Количество пусковых установок в одном канале обслуживания
· Количество взаимно помогающих каналов
· Зона обстрела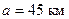
· Скорость движения самолетов противника
· Среднее расстояние между самолетами
· Количество каналов обслуживания

 

Расчетные характеристики:

	–	среднее число занятых каналов;
	–	вероятность обслуживания заявки;
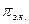
	–	вероятность занятости отдельного канала;

 

Создать аналитическую и имитационную модель СМО и проверить их адекватность.

 

Описание системы

Рассмотрим работу -канальной системы ПРО на вход которой поступают самолеты противника. Самолеты, пролетающие в пределах полосы налета, могут быть обстреляны любым из n каналов данной системы ПРО [1].

Ширина полосы налета определяется возможностями обстрела всеми n каналами любой цели в пределах полосы налета. Предполагается, что если самолет летит вне пределов полосы налета (слева или справа), тот эти самолеты не могут быть обстреляны ни одним из n каналов данной системы ПРО.

Глубина зоны обстрела определяется рубежом перехвата и рубежом прекращения огня, которые являются одинаковыми для всех n каналов. Если обозначить через среднюю дальность перехвата и через – среднюю дальность прекращения стрельбы, то можно записать следующее приближенное выражение для глубины зоны обстрела :

. (2.1)

Необходимо отметить, что характеристики зоны обстрела a и b зависят также от скорости налетающих самолетов , высоты их полета и т.п.

При анализе системы ПРО в качестве канала обслуживания рассматривается канал наведения. Так как в рассмотрении имеется система ПРО с частичной «взаимопомощью» между каналами, то предполагается, что несколько каналов могут обстреливать одну цель [1].

 

Рис. 2.1 -канальная система ПРО

 

Основный характеристикой системы ПРО является эффективная скорострельность одного канала (). Станция наведения (канал обслуживания) обеспечивается 2 пусковыми установками (), а каждая пусковая установка производит 0,75 выстрелов в минуту (). Тогда эффективная скорострельность одного канала определится так [1]:

, (2.2)

где – средняя вероятность поражения цели выпущенной по ней од ракетой; т.е.

При рассмотрении работы системы ПРО существенным является вопрос о получении информации о результатах стрельбы. Здесь возможны различные случаи.

Самым простым является случай, когда канал обслуживания обстреливает цель в течение времени 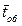после чего обстрел цели прекращается независимо от того, поражена цель или нет. Считая, что каждый из каналов производит пуассоновский поток эффективных (успешных) выстрелов с параметром , можно приближенно вычислить вероятность поражения цели одним каналом по формуле

. (2.3)

Если считать, что каждый канал производит регулярный поток выстрелов с параметром , то вероятность поражения цели одним таким каналом можно приближенно вычислить по формуле [1]:

. (2.4)

Если цель обстреливалась одновременно каналами и каждый из них поражает цель независимо от других, тут вероятность поражения цели будет равна:

. (2.5)

В рассматриваемом случае время обстрела должно быть меньше или по крайней мере равно времени пребывания цели в зоне обстрела 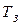. Среднее время пребывания цели в зоне обстрела будет [1]

, (2.6)

где – скорость полета самолета при условии, что он обстреливается.

Случай, когда , характерен для системы ПРО, когда само время 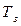мало и нет возможности выяснить, поражена ли цель или нет за время ее обстрела, т. е. когда цель находится в зоне обстрела очень малое время.

При анализе работы системы ПРО необходимо знать характеристики налета. Будем считать, что налетающие самолеты образуют пуассоновский поток с интенсивностью 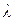, который определяется так:

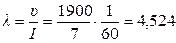
где – скорость движения самолетов противника,

– средний линейный интервал между самолетами.

Другой способ обстрела имеет место тогда, когда есть возможность получить и использовать информацию о поражении цели. Допустим, что время, проходящее между моментом поражения цели и моментом прекращения огня, есть случайная величина с математическим ожиданием . Если за начало отсчета времени считать момент входа самолета в зону обстрела, то при наличии свободных каналов это начало отсчета совпадает с началом обстрела цели. В общем случае время пребывания в зоне обстрела будет случайной величиной 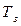с математическим ожиданием 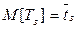. Цель будет не поражена, если время, требуемое для ее поражения , будет больше времени пребывания цели в зоне обстрела 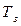. Если , то цель будет поражена. Время обстрела цели (или время занятости канала) в этом случае будет [1]:

, (2.7)

так как при всех условиях обстрел ведется до тех пор, пока цель находится в зоне обстрела. Если величина велика, то с большой вероятностью будет выполняться равенство , т.е. мы приходим к первому случаю обстрела цели, когда стрельба ведется в течение всего времени пребывания цели в зоне обстрела (типично для системы ПРО, у которой время 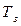мало).

Таким образом, вероятность поражения цели при условии, что она обстреливается одним каналом, будет определяться как вероятность выполнения неравенства [1]:

. (2.8)

Имея ввиду принятое допущение о пуассоновском характере системы, будем считать, что среднее время, затрачиваемое на поражение цели [1],

, (2.9)

а поток эффективных выстрелов является пуассоновским с параметром .

 

Разработка имитационной модели

Математическое описание

Имитационное моделирование основано на применении метода Монте-Карло, в котором используется искусственная реализация вероятностных законов. С помощью генератора псевдослучайных чисел вырабатываются независимые реализации случайного процесса, а интересующие нас характеристики находятся путем усреднения по всему множеству реализаций.

Исходные данные для имитационного моделирования:

· Дисциплина обслуживания – СМО с отказами и частичной взаимопомощью между каналами.

· – число каналов обслуживания;

· – интенсивность простейшего входящего потока заявок;

· – Интенсивность потока обслуживания заявок;

· – Интенсивность простейшего потока освобождения канала;

- параметр нетерпения заявки;

Интенсивности поступления и обслуживания заявок распределены по пуассоновскому закону.

При разработке имитационной модели для реализации входного потока заявок и потока обслуживания из равномерной случайной величины, генерируемой ЭВМ, необходимо получить случайную величину, распределенную по пуассоновскому закону. Пусть 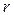– случайная величина, равномерно распределенная в интервале . Для пуассоновского распределения примем [1]

(3.1)

Осуществив интегрирование, получим [1]:

(3.2)

Решая это уравнение относительно , имеем [1]:

. (3.3)

Случайное число 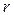распределено равномерно в интервале , следовательно также случайная величина, принадлежащая интервалу . Поэтому 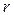и распределены одинаково. Отсюда имеем [1]:

. (3.4)

Определяемая этим соотношением случайная величина имеет пуассоновский закон распределения. Таким образом, интервал времени между заявками определяется следующим образом [1]:

, (3.5)

где – случайная величина в диапазоне , генерируемая ЭВМ.

Требуемые характеристики СМО можно определить следующим образом:

1) Вероятность обслуживания:

, (3.6)

где - количество обслуженных заявок; - общее количество заявок, пришедших в систему за время моделирования.

2) Вероятность занятости отдельного канала:

, (3.7)

3) Среднее число занятых каналов:

, (3.8)

где - интенсивность простейшего входящего потока заявок, - интенсивность потока обслуживания заявок.

Таким образом, используя имитационную модель можно получить требуемые параметры.

Имитационное моделирование включает следующие этапы [1]:

1. Построение входного потока заявок. Время появления заявки определяется следующим образом:

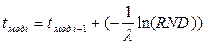, (3.9)

где 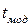– модельное время.

2. Обслуживание заявок. Для каждой заявки, стоящей на обслуживании, проверяется, не истекло ли время ее обслуживания. Если время истекло, то заявка считается обслуженной и занятые ей приборы освобождаются.

3. Генерация новой заявки. Генерируется время обслуживания пришедшей заявки, т.к. оно распределено по пуассоновскому закону, то время обслуживания:

, (3.10)

где – время обслуживания пришедшей заявки.

Далее заявка ставится на обслуживание, здесь возможны два варианта:

1) в системе свободно приборов и заявка обслуживается одновременно приборами. При этом заявка обслуживается параллельно, интенсивность обслуживания заявки увеличивается в раз;

2) число свободных приборов меньше . Заявка становится на обслуживание и обслуживается параллельно оставшимся числом приборов.

При моделировании используем программу для расчета имитационной модели (листинг программы см. Приложении 1).

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: