Анализ полученных результатов моделирования

Была исследована зависимость вероятностных характеристик системы от числа обслуживающих приборов. При увеличении числа обслуживающих приборов от 3 до 6 наблюдаем:

· уменьшение вероятности занятости канала;

· неизменность среднего времени занятости канала;

· увеличение среднего времени простоя канала.

В результате аналитического моделирования получены интересующие нас вероятностные характеристики системы. При аналитическом моделировании система ПРО рассматривалась в виде графа гибели и размножения, что позволило определить вероятности состояний из системы уравнений. Также эти характеристики могут быть посчитаны по заранее известным формулам. Расчет по эти формулам произведен в программе, листинг которой представлен в Приложении 2. Результаты аналитического моделирования представлены также в Приложении 3. А требуемые графики в Приложении 4.

 

Сопоставление полученных результатов для разработанных моделей

Что бы убедиться в адекватности применяемых моделей СМО, воспользуемся статистическим критерием 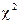, который служит для проверки однородности двух независимых выборок.

Если выборки однородны, то считают, что они извлечены из одной генеральной совокупности и, следовательно, имеют одинаковые, причем неизвестные, непрерывные функции распределения 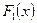и .

Таким образом, нулевая гипотеза состоит в том, что при всех значениях аргумента функции распределения равны между собой: .

Для того чтобы при заданном уровне значимости и количестве степеней свободы проверить нулевую гипотезу об однородности двух независимых выборок объемов и () при конкурирующей гипотезе 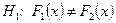необходимо найти величину 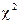по формуле [2]:

, (5.1)

и сравнить полученное значение с табличным для данных и .

Если , нулевую гипотезу отвергают.

Если 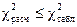, гипотеза об однородности выборок принимается.

Зададимся уровнем значимости (число степеней свободы ), при объеме выборки .

Значение для данных параметров равно 0,004.

В качестве 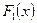выберем вероятность занятости канала обслуживания для аналитической модели, а – для имитационной модели.

Результаты расчетов сведем в таблицу.

Таблица 5.1.

Расчет значения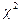

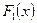
0,556	0,558
0,555	0,556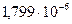
0,510	0,511
0,462	0,463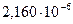

 

Из таблицы получили 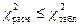, поэтому принимаем нулевую гипотезу об однородности выборок. Таким образом, результаты сравнения показывают адекватность моделей.

 

Заключение

В процессе выполнения данной индивидуальной работы была рассмотрена система массового обслуживания на примере системы ПРО с отказами и частичной взаимопомощью. Данная система ПРО была рассмотрена как система массового обслуживания с отказами и частичной взаимопомощью между каналами обслуживания.

Для заданной системы были построены две модели: аналитическая модель и имитационная модель. Обе системы рассматриваются при следующих упрощениях: рассматривается простейший пуассоновский поток входящих заявок, простейший пуассоновский поток обслуживания, а также система работает в стационарном режиме. В аналитической модели можно путем решения алгебраической системы уравнений можно определить вероятностные характеристики системы – вероятность обслуживания, вероятность занятости канала, среднее время простоя канала и др.

Имитационная модель строилась с учетом всех особенностей функционирования реальной системы и поэтому она достаточно точно описывает все вероятностные процессы. В основу имитационной модели положено рассмотрение работы системы на некотором отрезке времени. В результате этого можно определить вероятностные характеристики системы. Листинг программы имитационного моделирования приведен в Приложении 1.

На этапе сравнения двух построенных моделей с помощью критерия 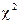были сделаны следующие вывод – с точки зрения вычисления такой характеристики системы как вероятность отказа модели (аналитическая и имитационная) адекватны.

Также была выявлена зависимость вероятностных характеристик системы от числа обслуживающих приборов, были получены следующие закономерности. Проводя моделирование при увеличении числа обслуживающих приборов от 3 до 6, наблюдаем:

· увеличение вероятности обслуживания;

· уменьшения вероятности занятости канала;

· увеличение среднего времени простоя канала.

Соответствующие зависимости в виде графиков представлены в Приложении 4.

 

Список используемой литературы

 

1. Южаков А.А. Прикладная теория систем массового обслуживания: Учеб. пособие, Пермь, Перм. гос. техн. ун-т, 2005.

2. Овчаров Л. А., Прикладные задачи теории массового обслуживания, Москва, Машиностроение, 1969.

3. Гмурман В. Е., Теория вероятностей и математическая статистика. М: Высшая школа, 2003.

4. ГОСТ 19.105-78. ЕСПД. Общие требования к программным документам.

 

Приложения

Приложение 1

Листинг программы имитационного моделирования

 

program SMO_im;

uses crt;

const

lambda=4.52; {Интенсивность простейшего входящего потока}

mu=0.975; {Интенсивность простейшего потока обслуживания}

eta=0.703; {Параметр нетерпимости заявки}

time_t=1000000; {Время моделирования}

n_kanalov=3; {Число каналов обслуживания}

l=3; {Параметр взаимопомощи}

var

n_svob,p:integer; {кол-во свободных в данный момент приборов}

vypolneno:real; {Количество выполненных заявок}

kolvo,otkaz:longint; {Кол-во заявок, кол-во отказов}

i,ok:integer;

t:longint; {Текущее время при моделировании}

t_z0,t_z,t_obs:real; {Интервалы обслуживания и занятости заявки}

n:array[1..n_kanalov] of real;{Массив, в котором хранится время занятости текущего канала}

t_zan:array[1..n_kanalov] of real;{Массив, в котором хранится общее время занятости каждого канала во время моделирования}

n_vyp:array[1..n_kanalov] of integer; {Массив, в котором хранится кол-во заявок, выполненных каждым каналом}

n_l_z:array[1..n_kanalov] of integer;

Pobs:real; {Вероятность обслуживания}

Lo,tpk,ksr:real; {Среднее число занятых каналов и плотность потока обслуживающих заявок}

n_zero:array[1..l] of integer; {Номера свободных в данный момент каналов обслуживания}

pobs,pzk:real; {Вероятность занятости канала}

begin

randomize;

t_z0:=0;

kolvo:=0;

otkaz:=0;

vypolneno:=0;

for i:=0 to n_kanalov do {Начальное обнуление параметров}

begin

n_vyp[i]:=0;

t_zan[i]:=0;

end;

for t:=0 to time_t do {Основной цикл моделирования}

begin

for i:=1 to n_kanalov do {Цикл проверки окончания обслуживания заявки}

begin

if ((t>=n[i])AND(n[i]<>0)) then {Если текущее время больше, чем}

begin

n[i]:=0;

vypolneno:=vypolneno+1/n_l_z[i];

n_l_z[i]:=0;

end;

продолжение Приложения 1

end;

if (t>=t_z0) then {Генерации прихода новой заявки}

begin

t_z:=-100/lambda*ln((random(1000)+1)/1000);{генерация случайного интервала между заявками}

t_z0:=t_z0+t_z;

inc(kolvo); {Счётчик числа пришедших заявок увеличивается на единицу}

n_svob:=0;

for i:=1 to l do n_zero[i]:=0; {Обнуляется массив номеров свободных каналов}

p:=1;

for i:=1 to n_kanalov do {Цикл поиска свободных каналов}

begin

if (n[i]=0) then

begin

inc(n_svob);

n_zero[p]:=i;

inc(p);

end;

end;

if (n_svob>=l) then begin {если число свободных каналов больше, чем l, то

поступившая заявка обслуживается l}

t_obs:=-100/(l*mu+eta)*ln((random(1000)+1)/1000);{Генерация времени обслуживания заявки}

for i:=1 to l do {Распределяем обслуживание заявки по l каналам}

begin

n[n_zero[i]]:=t+t_obs; {Записываем время окончания обслуживания заявки}

n_l_z[n_zero[i]]:=l;

t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;{Общее время занятости i-го канала}

n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1; {Число заявок, выполненных i-тым каналом}

ok:=1; {Заявка поставлена на обслуживание}

end;

end

else

if (n_svob>0)AND(n_svob<l) then begin {если число свободных каналов меньше, чем l, то поступившая заявка обслуживается}

t_obs:=-100/(n_svob*mu+eta)*ln((random(1000)+1)/1000); {Генерация времени обслуживания заявки}

for i:=1 to n_svob do {Распределяем обслуживание заявки по оставшимся свободным каналам}

begin

n[n_zero[i]]:=t+t_obs; {Записываем время окончания обслуживания заявки}

n_l_z[n_zero[i]]:=n_svob;

t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;{Общее время занятости i-го

канала}

n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1; {Число заявок, выполненных i-тым

каналом}

ok:=1; {Заявка поставлена на обслуживание}

end;

продолжение Приложения 1

end

else ok:=0; {иначе заявка не поставлена на обслуживание}

if (ok<>1) then inc(otkaz); {Если заявка не поставлена на обслуживание, то увеличивается счётчик отказов на единицу}

end;

end; {Окончание основного цикла моделирования}

{Вычисление интересующих параметров по результатам моделирования}

pzk:=0;

for i:=1 to n_kanalov do pzk:=pzk+t_zan[i]/time_t;

pzk:=pzk/n_kanalov; {Вычисление вероятности занятости канала}

tpk:=0;

for i:=1 to n_kanalov do if (n_vyp[i]<>0) then tpk:=tpk+(time_t-t_zan[i])/n_vyp[i];

ksr:=pzk*n_kanalov; {Вычисление среднего числа занятых каналов}

Pobs:=(kolvo-otkaz)/kolvo; {Вычисление вероятности обслуживания}

writeln('Число заявок ',kolvo);

writeln('Выполнено ',vypolneno:5:0);

writeln('Вероятность обслуживания ',Pobs:5:3); {Вывод результатов моделирования}

writeln('Вероятность занятости канала ',pzk:5:3);

writeln('Среднее число занятых каналов ',ksr:5:3);

readln;

end.

 

Приложение 2

Листинг программы аналитического моделирования

 

program SMO_an;

uses crt;

const l=4.52;

m=0.703;

n=6;

ll=3;

k=2000;

function faktorial(a:integer):integer;

var ii,fak:integer;

 

begin

fak:=1;

if a=0 then fak:=1;

for ii:=1 to a do fak:=fak*ii;

faktorial:=fak;

end;

 

var

p: array [0..n] of real;

i,h,ns:integer;

c:real;

 

begin

h:=n div ll;

ns:=h;

c:=0;

if n mod ll <>0 then ns:=ns+1;

for i:=0 to ns do p[i]:=0;

for i:=0 to ns-1 do c:=c+exp(i*ln(l))/(faktorial(i)*exp(i*ln(ll*m)));

c:=c+exp(ns*ln(l))/(faktorial(ns-1)*n*m*exp((ns-1)*ln(ll*m)));

p[0]:=1/c;

for i:=1 to ns-1 do p[i]:=(p[i-1]*l)/(i*ll*m);

{exp(i*ln(l))/(faktorial(i)*exp(i*ln(ll*m))*c);}

 

p[ns]:=p[ns-1]*l/(n*m);

{exp(ns*ln(l))/(faktorial(ns)*m*exp((ns-1)*ln(ll*m))*c);}

for i:=0 to ns do writeln('p[',i,']=',p[i]:4:5);

writeln('n=',ns);

writeln('Pobsl=',(1-p[ns]):3:6);

writeln('l0=',(1-p[ns]):3:6);

writeln('ksr=',(l/m)*p[ns]:3:6);

readln;

end.

Приложение 3

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: