 |
Математическое описание аналитической модели
|
|
|
|
Рассмотрим заданную систему массового обслуживания – систему ПРО с отказами и частичной взаимопомощью между каналами (при рассмотрении ПРО взаимопомощь между каналами состоит в том, что одну цель могут одновременно обстреливать 
каналов, при этом эффективная скорострельность увеличивается в раз).
На вход n -канальной системы массового обслуживания поступает простейший поток заявок с плотностью 
. Плотность простейшего потока обслуживаний каждого канала 
. Если поступившая на обслуживание заявка застает все каналы свободными, то она принимается на обслуживание и обслуживается одновременно каналами (
). При этом поток обслуживаний одной заявки будет иметь интенсивность 
.
Если поступившая на обслуживание заявка застает в системе одну заявку, то при 
вновь прибывшая заявка будет принята к обслуживанию и будет обслуживаться одновременно каналами.
Если поступившая на обслуживание заявка застает в системе 
заявок (
), при этом 
, то поступившая заявка будет обслуживаться каналами с общей производительностью . Если вновь поступившая заявка застает в системе 
заявок и при этом выполняются совместно два неравенства 
и 
, то заявка будет принята на обслуживание. В этом случае заявки, находившиеся на обслуживании будут обслуживаться каналами, а вновь пришедшая заявка – меньшим, чем , числом каналов, но в обслуживании будут заняты все n каналов. Если вновь поступившая заявка застает в системе все каналы занятыми, то она получает отказ и не обслуживается. Попавшая на обслуживание заявка обслуживается до конца (заявки «терпеливые»).
Исходные данные для имитационного моделирования:
· 
– интенсивность простейшего входящего потока заявок;
|
|
|
· 
– Интенсивность потока обслуживания заявок;
· 
– Интенсивность простейшего потока освобождения канала;
- параметр нетерпения заявки;
· 
– число каналов обслуживания;
Такой системе соответствует следующий граф (входящий поток и поток обслуживания – Пуассоновские, режим работы – стационарный).
За состояние системы принимается число заявок, находящихся в данный момент на обслуживании в системе [1]:
Рис. 4.1 Граф состояний системы ПРО с отказами и частичной взаимопомощью между каналами
. Если в системе 
заявок, то 
заявка обслуживается приборами, а 
заявка – 
приборами.
Можно записать систему алгебраических уравнений в общем виде [1]:
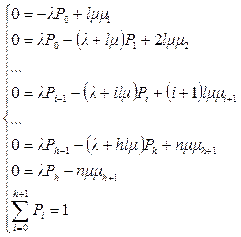(4.1)
– вероятность того, что система находится в состоянии 
.
Последнее уравнение системы представляет собой условие нормировки, так как мы имеем дело с полной группой событий. Решив данную систему алгебраических уравнений можно найти вероятности нахождения системы в каждом из состояний.
Заметим, что граф состояний системы до состояния 
, с точностью до обозначений параметров потоков совпадает с графом состояний классической системы массового обслуживания с отказами.
Следовательно [1]:
(4.2)
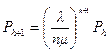(4.3)
Введем обозначения: 
, тогда:
С учетом нормировочного условия, получаем [1]:
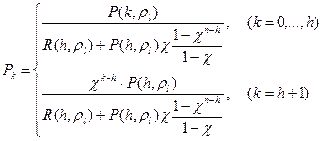(4.4)
где 
.
Для сокращения дальнейшей записи введем обозначение [1]
(4.5)
Формулы расчетных характеристик для нашего случая будут выглядеть так:
1) Вероятность обслуживания заявки (вероятность поражения самолёта):
, (4.6)
2) Среднее число занятых каналов обслуживания:
(4.7)
3) Вероятность занятости канала:
. (4.8)
Расчет параметров СМО
Рассмотрим граф состояний для нашего конкретного случая, т.е. количество каналов обслуживания 
, а количество взаимодействующих каналов 
.
1. Для 
,
– граф состояний
Рис. 4.2 Граф состояний 3-х канальной системы ПРО
где Х0 – заявки в системе отсутствуют;
|
|
|
Х1 – в системе находится одна заявка (занято 3 канала);
– система уравнений
(4.9)
Вероятность обслуживания: 
Вероятность занятости канала: 
Среднее число занятых каналов: 
2. Для 
, :
– граф состояний
Рис. 4.3 Граф состояний 4-х канальной системы ПРО
где Х0 – заявки в системе отсутствуют;
Х1 – в системе находится одна заявка (занято 3 канала);
Х2 – в системе находится две заявки (занято 3 канала, вторая заявка обслуживается одним прибором);
– система уравнений
(4.10)
Вероятность обслуживания: 
Вероятность занятости канала: 
Среднее число занятых каналов: 
3. Для 
, :
– граф состояний
Рис. 4.4 Граф состояний 5-и канальной системы ПРО
где Х0 – заявки в системе отсутствуют;
Х1 – в системе находится одна заявка (занято 3 канала);
Х2 – в системе находится две заявки (занято 5 каналов одна обслуживается двумя каналами другая тремя);
– система уравнений
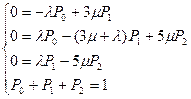(4.11)
Вероятность обслуживания: 
Вероятность занятости канала: 
Среднее число занятых каналов: 
4. Для 
, :
– граф состояний
Рис. 4.5 Граф состояний 6-и канальной системы ПРО
где Х0 – заявки в системе отсутствуют;
Х1 – в системе находится одна заявка (занято 3 канала);
Х2 – в системе находится две заявки (занято 6 каналов каждая заявка обслуживается 3-мя приборами);
– система уравнений
(4.12)
Вероятность обслуживания: 
Вероятность занятости канала: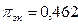 
Среднее число занятых каналов: 
При решении системы уравнений вероятностных состояний используем программу для расчета аналитической модели (листинг программы см. Приложение 1). Результаты вычислений представлены в табл.1
|
|
|
