 |
Показатели надежности восстанавливаемых объектов
|
|
|
|
Рассматриваемые в гл. 3 показатели надежности характеризуют только процессы отказов. Для оценки надежности объектов многоразового использования необходимы дополнительные показатели, учитывающие также процессы восстановления (ремонта) элементов (объектов).
Параметр потока отказов  (t) — математическое ожидание числа отказов, происшедших за единицу времени, начиная с момента t при условии, что все элементы, вышедшие из строя, заменяются работоспособными, т. е. число наблюдаемых элементов сохраняется одинаковым в процессе эксплуатации.
(t) — математическое ожидание числа отказов, происшедших за единицу времени, начиная с момента t при условии, что все элементы, вышедшие из строя, заменяются работоспособными, т. е. число наблюдаемых элементов сохраняется одинаковым в процессе эксплуатации.
Для экспоненциального закона надежности интенсивность и параметр потока отказов не зависят от времени и совпадают, т. е.
 .
.
Вероятность восстановления S(t)— вероятность того, что отказавший элемент будет восстановлен в течение заданного времени t, т. е. вероятность своевременного завершения ремонта.
Очевидно то, что
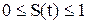 , S(0)=0, S(
, S(0)=0, S( )=1.
)=1.
Для определения величины S(t) используется следующая статистическая оценка:
S(t)=  , (4.1)
, (4.1)
где N  (0) – число элементов, поставленных на восстановление в начальный момент времени t = 0; N
(0) – число элементов, поставленных на восстановление в начальный момент времени t = 0; N  – число элементов, время восстановления которых оказалось меньше заданного времени t, т. е. восстановленных на интервале (0,t).
– число элементов, время восстановления которых оказалось меньше заданного времени t, т. е. восстановленных на интервале (0,t).
Вероятность невосстановления (несвоевременного завершения ремонта) G(t) - вероятность того, что отказавший элемент не будет восстановлен в течение заданного времени t.
Статистическая оценка величины G(t):
G(t)=  . (4.2)
. (4.2)
Из анализа выражений (4.1) и (4.2) следует, что всегда
S(t)+G(t)=1.
На рис. 4.1 в графической форме представлены изменения S(t) и G(t) во времени.
Частота восстановления a  (t) – производная от вероятности восстановления:
(t) – производная от вероятности восстановления:
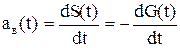 . (4.3)
. (4.3)
Для численного определения величины ав(t) используется её статистическая оценка
|
|
|
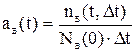 , (4.4)
, (4.4)
где  – число восстановленных элементов на интервале времени от t до t +
– число восстановленных элементов на интервале времени от t до t + 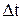 .
.

Рис. 4.1
Интенсивность восстановления  (t) — условная вероятность восстановления после момента t за единицу времени
(t) — условная вероятность восстановления после момента t за единицу времени 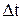 при условии, что до момента t восстановления элемента не произошло.
при условии, что до момента t восстановления элемента не произошло.
Интенсивность восстановления связана с частотой восстановления:
 . (4.5)
. (4.5)
Статистически интенсивность восстановления определяется следующим образом:
 . (4.6)
. (4.6)
Сравнение формул для определения частоты (4.4) и интенсивности (4.6) восстановления показывает, что они отличаются числом элементов в знаменателе.
В отличие от процесса отказов, который развивается во времени естественным образом, процесс восстановления является целиком искусственным (ремонт элемента) и тем самым полностью определяется организационно-технической деятельностью эксплуатационного персонала. Поэтому кривая интенсивности восстановления, аналогичная кривой интенсивности отказов, здесь отсутствует. Так как установлены обоснованные нормативы времени на проведение ремонтных работ, то принимают интенсивность восстановления независимой от времени:  . Численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов.
. Численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов.
Для экспоненциального распределения времени восстановления, т.е. при постоянной интенсивности восстановления, по аналогии с процессом отказов (формулы (3.10) и (3.11)) имеем следующие зависимости:
S(t)=1-exp(-  t), (4.7)
t), (4.7)
G(t)=exp(-  t). (4.8)
t). (4.8)
Среднее время восстановления T  представляет собой математическое ожидание времени восстановления и численно соответствует площади под кривой вероятности невосстановления:
представляет собой математическое ожидание времени восстановления и численно соответствует площади под кривой вероятности невосстановления:
T  =
=  G(t)dt. (4.9)
G(t)dt. (4.9)
Статистическая оценка величины T  :
:
 , (4.10)
, (4.10)
где  – длительность восстановления i-го элемента (объекта).
– длительность восстановления i-го элемента (объекта).
Для отдельно рассматриваемого элемента под  понимается длительность восстановления после i-го отказа, а под
понимается длительность восстановления после i-го отказа, а под  – число отказов данного элемента.
– число отказов данного элемента.
|
|
|
При экспоненциальном распределении времени восстановления, когда интенсивность восстановления  = const, аналогично (3.16) имеем соотношение
= const, аналогично (3.16) имеем соотношение
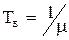 , (4.11)
, (4.11)
т.е. среднее время восстановления численно равно средней по множеству однотипных элементов (объектов) продолжительности восстановления, приходящейся на один объект. Поскольку  = const, то и T
= const, то и T  = const.
= const.
В табл. 4.1 сведены показатели надежности, характеризующие процесс выхода из строя элементов, и аналогичные им показатели, характеризующие встречный процесс восстановления элементов.
Таблица 4.1
| Процесс отказов | Процесс восстановления | ||
| Вероятность безотказной работы | P(t) | Вероятность невосстановления | G(t) |
| Вероятность отказа | Q(t) | Вероятность восстановления | S(t) |
| Частота отказов | a(t) | Частота восстановления | a  (t) (t)
|
| Интенсивность отказов | 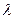 (t) (t)
| Интенсивность восстановления | 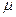 (t) (t)
|
| Средняя наработка на отказ | T | Среднее время восстановления | T 
|
В случае, когда требуется оценить надежность работы элемента безотносительно к времени его работы, используются рассматриваемые ниже показатели.
Коэффициент готовности K  – вероятность того, что элемент работоспособен в произвольный момент времени.
– вероятность того, что элемент работоспособен в произвольный момент времени.
Для определения величины K  отдельного элемента используется следующая статистическая оценка:
отдельного элемента используется следующая статистическая оценка:
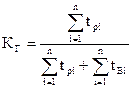 , (4.12)
, (4.12)
где t  – i-й интервал времени исправной работы элемента, t
– i-й интервал времени исправной работы элемента, t  – i-й интервал времени восстановления элемента после i-го отказа, n – число отказов.
– i-й интервал времени восстановления элемента после i-го отказа, n – число отказов.
Разделив численно знаменатель выражения (4.12) на число отказов n, происшедших за рассматриваемое время, получим следующее выражение:
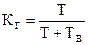 . (4.13)
. (4.13)
Таким образом, коэффициент готовности равен вероятности пребывания элемента в работоспособном состоянии в произвольный момент времени в рассматриваемом периоде.
Коэффициент готовности имеет смысл надежностного коэффициента полезного действия, так как числитель представляет собой полезную составляющую, а знаменатель – общие затраты времени.
Коэффициент готовности является важным показателем надежности, так как характеризует готовность элемента к работе и позволяет также оценить его эксплуатационные качества (удобство эксплуатации, стоимость эксплуатации) и требуемую квалификацию обслуживающего персонала.
|
|
|
Коэффициент простоя Кп – вероятность того, что элемент неработоспособен в любой момент времени.
Статистическая оценка величины Кп:
 (4.14)
(4.14)
По аналогии с коэффициентом готовности получаем зависимость для коэффициента простоя:
 (4.15)
(4.15)
Очевидно, что всегда имеет место равенство
 . (4.16)
. (4.16)
Относительный коэффициент простоя  – отношение коэффициента простоя к коэффициенту готовности:
– отношение коэффициента простоя к коэффициенту готовности:
 . (4.17)
. (4.17)
Коэффициент технического использования  учитывает дополнительные преднамеренные отключения элемента, необходимые для проведения планово-предупредительных ремонтов:
учитывает дополнительные преднамеренные отключения элемента, необходимые для проведения планово-предупредительных ремонтов:
 (4.18)
(4.18)
где 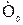 – среднее время обслуживания, т.е. среднее время нахождения элемента в отключенном состоянии для производства планово-предупредительных ремонтов (профилактики).
– среднее время обслуживания, т.е. среднее время нахождения элемента в отключенном состоянии для производства планово-предупредительных ремонтов (профилактики).
Коэффициент оперативной готовности Ког – вероятность того, что элемент работоспособен в произвольный момент времени t и безошибочно проработает в течение заданного времени  (t,t+
(t,t+  ):
):
 (4.19)
(4.19)
Для определения величины  используется статистическая оценка
используется статистическая оценка
 (4.20)
(4.20)
где  – число элементов, исправных в момент времени t и безотказно проработавших в течение времени
– число элементов, исправных в момент времени t и безотказно проработавших в течение времени  , N(0) – первоначальное число наблюдаемых элементов в момент времени t = 0.
, N(0) – первоначальное число наблюдаемых элементов в момент времени t = 0.
Коэффициент оперативной готовности позволяет количественно оценить надежность объекта в аварийных условиях, т.е. до окончания выполнения какой-то эпизодической функции.
Пример 4.1
Проводилось наблюдение за работой элемента на интервале времени t = 1300 ч, в течение которого было зафиксировано N(0)=14 отказов. Требуется определить среднюю наработку на отказ, если известно среднее время восстановления 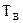 =2 ч, а вывод элемента из работы для проведения профилактических ремонтов не производился.
=2 ч, а вывод элемента из работы для проведения профилактических ремонтов не производился.
Решение
Используем формулу (3.17). С учетом времени восстановления элемента после отказов получаем
T=  .
.
Пример 4.2
Определить коэффициенты готовности, простоя и коэффициент технического использования для трансформатора с высшим напряжением 35, 110 кВ.
|
|
|
Решение
Из табл. 3.2 берем исходные показатели надежности (для резервированной системы):
 ,
, 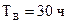 ,
, 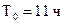 .
.
Тогда Т =  = 1/0,03 = 33,33 года.
= 1/0,03 = 33,33 года.
Расчеты по формулам (4.13), (4.16), (4.18) дают следующие результаты:
К  =
=  =0,999897; К
=0,999897; К 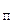 =1-0,999897=0,000103;
=1-0,999897=0,000103; 
 =0,999859.
=0,999859.
|
|
|


