 |
Теорема умножения вероятностей
|
|
|
|
Предварительно введем понятие о зависимых и независимых событиях.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события А, вычисленная при условии, что имело место событие В, называется условной вероятностью события А и обозначается Р(А\В).
Теорема умножения вероятностей формулируется следующим образом: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место, т.е.
р(АВ)=р(А)р(В\А)=р(В)р(А\В). (5.4)
Из теоремы умножения вероятностей следует, что если событие А не зависит от события В, то и событие В не зависит от события А, т.е. если р(А)=р(А\В), то р(В)=р(В\А). Таким образом, зависимость или независимость событий всегда взаимны. В связи с этим можно дать следующее новое определение независимых событий: два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Вероятность произведения двух независимых событий равна произведению вероятности этих событий:
р(АВ)=р(А)р(В). (5.5)
Для n независимых событий
Р(С)=р  (А
(А  )р
)р  (А
(А  )...р
)...р 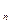 (А
(А 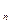 ), (5.6)
), (5.6)
т.е. вероятность произведения независимых событий равна произведению вероятностей этих событий.
Надежность систем с последовательным соединением элементов
|
|
|
Последовательным (основным) называется соединение элементов, при котором выход из строя хотя бы одного из них приводит к отказу всей системы, т.е. последовательная структура работоспособна, если все ее элементы работоспособны.
Следует отметить, что в производственной системе элементы физически могут быть соединены и параллельно, однако по надежности они при этом могут соединяться как параллельно, так и последовательно.
Схема замещения (по надежности) системы с последовательной структурой представлена на рис. 5.1.

Рис. 5.1
Предполагая, что отказы элементов являются независимыми событиями, определяем на основе формулы (5.6) вероятность работоспособности (безотказной работы) последовательной структуры по формуле
 (5.7)
(5.7)
где P 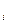 (t) – вероятность безотказной работы i-го элемента, n – число элементов.
(t) – вероятность безотказной работы i-го элемента, n – число элементов.
Вероятность отказа последовательной структуры
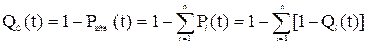 , (5.8)
, (5.8)
где Q 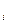 – вероятность отказа i-го элемента.
– вероятность отказа i-го элемента.
Если все элементы равнонадежны, т.е.
 ,
,  ,
,
то формулы (5.7) и (5.8) принимают вид:
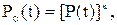 (5.9)
(5.9)
 . (5.10)
. (5.10)
Формулу (5.7) с учетом зависимости (3.11) можно представить в виде
 , (5.11)
, (5.11)
где  (x) – интенсивность отказов i-го элемента.
(x) – интенсивность отказов i-го элемента.
Для экспоненциального закона распределения времени безотказной работы, т.е. при постоянной во времени интенсивности отказов каждого элемента, формула (5.11) упрощается и принимает вид
 ). (5.12)
). (5.12)
Интенсивность отказов системы с последовательной структурой в целом на основании формул (3.13) и (5.12) можно определить по формуле
 . (5.13)
. (5.13)
Среднее время безотказной работы системы с учетом формул (3.16) и (5.13) рассчитывается как
 , (5.14)
, (5.14)
где Т 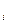 – среднее время безотказной работы i-го элемента.
– среднее время безотказной работы i-го элемента.
Среднее время восстановления системы
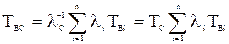 , (5.15)
, (5.15)
где Т  – время восстановления i-го элемента, является математическим ожиданием времени восстановления, взвешенным по интенсивности отказов n последовательно соединенных элементов.
– время восстановления i-го элемента, является математическим ожиданием времени восстановления, взвешенным по интенсивности отказов n последовательно соединенных элементов.
|
|
|
Пример 5.1
Определить интенсивность отказов, среднее время восстановления, среднее время безотказной работы и вероятность безотказной работы в течение 1 года системы, состоящей из пяти последовательно соединенных элементов со следующими показателями надежности:
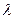
 =0,50 год-1, T
=0,50 год-1, T 
 ;
;
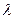
 =0,32 год-1, T
=0,32 год-1, T 
 ;
;
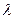
 =0,30 год-1, T
=0,30 год-1, T 
 ;
;
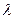
 =0,64 год-1, T
=0,64 год-1, T 
 ;
;
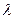
 =0,001 год-1, T
=0,001 год-1, T 
 .
.
Решение
Интенсивность отказов системы
 =0,50+0,32+0,30+0,64+0,001=1,761 год-1.
=0,50+0,32+0,30+0,64+0,001=1,761 год-1.
Среднее время восстановления
 (0,50 × 16,0 + 0,32 × 8,0 + 0,30 × 6,0 + 0,64 × 12,5 +
(0,50 × 16,0 + 0,32 × 8,0 + 0,30 × 6,0 + 0,64 × 12,5 +
+ 0,001 × 15,0) = 11,57 ч.
Среднее время безотказной работы
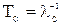 = 1/1,761 = 0,568 год = 4974 ч.
= 1/1,761 = 0,568 год = 4974 ч.
Вероятность безотказной работы за t = 1 год.
 = ехр(-1,761 1) = 0,17.
= ехр(-1,761 1) = 0,17.
Надежность систем с параллельным соединением элементов
Параллельным соединением называется структура, отказ которой наступает при отказе всех элементов, входящих в структуру.
Параллельную структуру называют также избыточной или резервированной, поскольку она содержит элементов больше, чем это необходимо для ее нормальной работы. При отказе одного или нескольких элементов функция структуры выполняется оставшимися в работе элементами, если последние удовлетворительно выполняют функции отказавших.
Схема замещения (по надежности) системы с параллельной структурой представлена на рис. 5.2.
В общем случае отказ параллельной структуры предполагает, что все m элементов находятся в состоянии простоя, т.е.
 (5.16)
(5.16)

Рис. 5.2
Вероятность безотказной работы системы
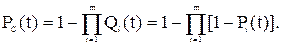 (5.17)
(5.17)
При равнонадежных элементах  имеем
имеем
 (5.18)
(5.18)
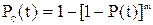 . (5.19)
. (5.19)
Как и для систем с последовательным соединением элементов, здесь предполагается независимость отказов всех элементов. Кроме того, пропускная способность элементов не ограничивается.
Число параллельно соединенных элементов в СЭС редко бывает больше трех. Вероятность того, что будут работать один или два элемента (при m = 2), в соответствии с формулой (5.3) рассчитывается как
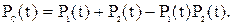 (5.20)
(5.20)
Вероятность отказа обоих элементов
 . (5.21)
. (5.21)
Виды резервирования
На стадии проектирования СЭС для обеспечения требуемой надежности приходится во многих случаях как минимум дублировать отдельные элементы и даже отдельные системы, т.е. использовать резервирование.
|
|
|
Резервирование характерно тем, что оно позволяет повысить надежность системы по сравнению с надежностью составляющих ее элементов. Повышение надежности отдельно взятых элементов требует больших материальных затрат.
В этих условиях резервирование, например, за счет введения дополнительных элементов, является эффективным средством обеспечения требуемой надежности систем.
Если при последовательном соединении элементов общая надежность системы (т.е. вероятность безотказной работы) ниже надежности самого ненадежного элемента, то при резервировании общая надежность системы может быть выше надежности самого надежного элемента.
Резервирование осуществляется путем введения избыточности. В зависимости от природы последней резервирование бывает:
• структурное (аппаратное);
• информационное;
• временное.
Структурное резервирование заключается в том, что в минимально необходимый вариант системы, состоящей из основных элементов, вводятся дополнительные элементы, устройства или даже вместо одной системы предусматривается использование нескольких одинаковых систем.
Информационное резервирование предусматривает использование избыточной информации. Его простейшим примером является многократная передача одного и того же сообщения по каналу связи. Другим примером являются коды, применяемые в управляющих ЭВМ для обнаружения и исправления ошибок, возникающих в результате сбоев и отказов аппаратуры.
Временное резервирование предусматривает использование избыточного времени. Возобновление прерванного в результате отказа функционирования системы происходит путем ее восстановления, если имеется определенный запас времени.
Существуют два метода повышения надежности систем путем структурного резервирования:
1) общее резервирование, при котором резервируется система в целом;
2) раздельное (поэлементное) резервирование, при котором резервируются отдельные части (элементы) системы.
Схемы общего и раздельного структурного резервирования представлены соответственно на рис. 5.3 и 5.4, где n - число последовательных элементов в цепи, m – число резервных цепей (при общем резервировании) или резервных элементов для каждого основного (при раздельном резервировании).
|
|
|
При m = 1 имеет место дублирование, а при m=2 – троирование. Обычно стремятся по возможности применять раздельное резервирование, т.к. при этом выигрыш в надежности часто достигается значительно меньшими затратами, чем при общем резервировании.
В зависимости от способа включения резервных элементов различают постоянное резервирование, резервирование замещением и скользящее резервирование.
Постоянное резервирование – это такое резервирование, при котором резервные элементы участвуют в работе объекта наравне с основными. В случае отказа основного элемента не требуется специальных устройств, вводящих в действие резервный элемент, поскольку он включается в работу одновременно с основным.
Резервирование замещением – это такое резервирование, при котором функции основного элемента передаются резервному только после отказа основного. При резервировании замещением необходимы контролирующие и переключающие устройства для обнаружения факта отказа основного элемента и переключения с основного на резервный.
 |
Рис. 5.4
Скользящее резервирование – представляет собой разновидность резервирования замещением, при котором основные элементы объекта резервируются элементами, каждый из которых может заменить любой отказавший элемент.
Оба вида резервирования (постоянное и замещением) имеют свои преимущества и недостатки.
Достоинством постоянного резервирования является простота, т.к. в этом случае не требуются контролирующие и переключающие устройства, понижающие надежность системы в целом, и, самое главное, отсутствует перерыв в работе. Недостатком постоянного резервирования является нарушение режима работы резервных элементов при отказе основных.
Включение резерва замещением обладает следующим преимуществом: не нарушает режима работы резервных элементов, сохраняет в большей степени надежность резервных элементов, позволяет использовать один резервный элемент на несколько рабочих (при скользящем резервировании).
В зависимости от режима работы резервных элементов различают нагруженный (горячий) и ненагруженный (холодный) резерв.
Нагруженный (горячий) резерв в энергетике называют также вращающимся или включенным. В данном режиме резервный элемент находится в том же режиме, что и основной. Ресурс резервных элементов начинает расходоваться с момента включения в работу всей системы и вероятность безотказной работы резервных элементов в этом случае не зависит от того, в какой момент времени они включаются в работу.
|
|
|
Облегченный (теплый) резерв характеризуется тем, что резервный элемент находится в менее нагруженном режиме, чем основной. Поэтому, хотя ресурс резервных элементов также начинает расходоваться с момента включения всей системы в целом, интенсивность расхода ресурса резервных элементов до момента их включения вместо отказавших значительно ниже, чем в рабочих условиях. Этот вид резерва обычно размещается на агрегатах, работающих на холостом ходу, и, следовательно, в данном случае ресурс резервных элементов срабатывается меньше
по сравнению с рабочими условиями, когда агрегаты несут нагрузку. Вероятность безотказной работы резервных элементов в случае этого вида резерва будет зависеть как от момента их включения в работу, так и от того, насколько отличаются законы распределения вероятности безотказной работы их в рабочем и резервном условиях.
В случае ненагруженного (холодного) резерва резервные элементы начинают расходовать свой ресурс с момента их включения в работу вместо основных. В энергетике этим видом резерва служат обычно отключенные агрегаты.
Расчеты надежности систем с параллельно включенными элементами зависят от способа резервирования.
Надежность систем при постоянном общем резервировании
Будем считать, что резервируемые и резервные элементы равнонадежны, т.е.  и
и 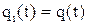 . Для удобства вероятности безотказной работы и появления отказов отдельных элементов обозначаем в этой и последующих главах прописными буквами.
. Для удобства вероятности безотказной работы и появления отказов отдельных элементов обозначаем в этой и последующих главах прописными буквами.
С учетом схемы замещения (рис. 5.5) и формулы (5.18) вероятность отказа системы с m резервными цепями можно рассчитать следующим образом:
 , (5.22)
, (5.22)
где  (t) – вероятность отказа основной цепи,
(t) – вероятность отказа основной цепи, 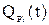 – вероятность отказа i-й резервной цепи.
– вероятность отказа i-й резервной цепи.
Соответственно вероятность безотказной работы системы
 (5.23)
(5.23)
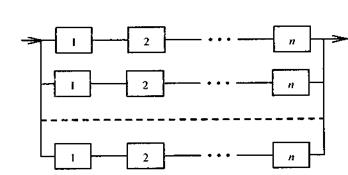
Рис. 5.5
В соответствии с формулой (5.8) имеем
 (5.24)
(5.24)
При одинаковых вероятностях отказов основной и резервной цепей  формулы (5.22) и (5.23) принимают вид:
формулы (5.22) и (5.23) принимают вид:
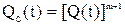 , (5.25)
, (5.25)
 . (5.26)
. (5.26)
Среднее время безотказной работы системы при общем резервировании
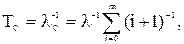 (5.27)
(5.27)
где 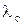 – интенсивность отказов системы,
– интенсивность отказов системы,  – интенсивность отказов любой из (m+1) цепей,
– интенсивность отказов любой из (m+1) цепей, 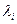 – интенсивность отказов i-го элемента.
– интенсивность отказов i-го элемента.
Для системы из двух параллельных цепей (m=1) формула (5.27) принимает вид
 . (5.28)
. (5.28)
Среднее время восстановления системы в общем случае определяется по формуле
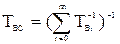 , (5.29)
, (5.29)
где  – среднее время восстановления i-й цепи.
– среднее время восстановления i-й цепи.
Для частного случая m = 1 формула (5.29) принимает вид
 (5.30)
(5.30)
Пример 5.2
Рассчитать вероятность безотказной работы в течение 3 месяцев, интенсивность отказов, среднюю наработку на отказ одноцепной ВЛ длиной l = 35 км вместе с понижающим трансформатором 110/10 кВ и коммутационной аппаратурой (рис. 5.6).

Рис. 5.6
Решение
Схема замещения по надежности рассматриваемой СЭС представляет собой последовательную структуру (рис. 5.7).

Рис. 5.7
Интенсивности отказов элементов взяты из табл. 3.2:
 ;
; 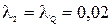
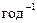 ;
;
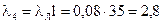
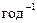 ;
; 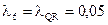
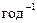 ;
;

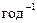 ;
; 
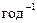 .
.
Согласно формуле (5.7) определяем интенсивность отказов схемы питания:

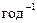 .
.
Этот расчет показывает, что доминирующее влияние на выход схемы из строя оказывает повреждаемость воздушной линии. Средняя наработка на отказ схемы питания
 .
.
Вероятность безотказной работы схемы в течение t = 0,25 год.

Пример 5.3
Определить, насколько выше показатели надежности понизительной трансформаторной подстанции 110/10 кВ при постоянной совместной работе обоих трансформаторов в течение 6 месяцев по сравнению с однотрансформаторной подстанцией. Отказами коммутационных аппаратов и преднамеренными отключениями пренебрегаем.
Решение
Исходные данные, взятые из табл. 3.2, следующие:
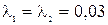
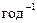 ;
; 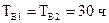 .
.
Вероятность безотказной работы в течение 6 месяцев одного трансформатора

Средняя наработка на отказ одного трансформатора
 год.
год.
Вероятность безотказной работы двухтрансформаторной подстанции, рассчитанная по формуле (5.20):
 .
.
Средняя наработка на отказ двухтрансформаторной подстанции, рассчитанная по формуле (5.28):
 лет.
лет.
Интенсивность отказов двухтрансформаторной подстанции

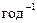 .
.
Среднее время восстановления двухтрансформаторной подстанции (формула (5.30)).
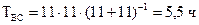 .
.
Анализ результатов показывает, что надежность двухтрансформаторной подстанции намного превышает надежность однотрансформаторной подстанции.
Пример 5.4
 Рассмотрим секцию РУ 6 кВ, от которой питаются 18 отходящих линий
Рассмотрим секцию РУ 6 кВ, от которой питаются 18 отходящих линий
(рис. 5.8). Интенсивность отказов выключателей, сопровождающихся короткими замыканиями, оценивается величиной
 = 0,003
= 0,003 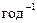 , интенсивность отказов с короткими замыканиями для сборных шин на одно присоединение
, интенсивность отказов с короткими замыканиями для сборных шин на одно присоединение  (см. табл. 3.2). Определить интенсивность кратковременных погашений секции РУ, предполагая абсолютную надежность автоматического ввода резерва (АВР) и выключателя Q2, резервирующего питание секции.
(см. табл. 3.2). Определить интенсивность кратковременных погашений секции РУ, предполагая абсолютную надежность автоматического ввода резерва (АВР) и выключателя Q2, резервирующего питание секции.

Решение
Схема замещения по надежности секции РУ представляет собой последовательное соединение элементов (рис. 5.9), число которых равно общему числу выключателей, не считая Q2.

Рис. 5.9
Интенсивность кратковременных погашений секции РУ 6 кВ из-за коротких замыканий на выключателях и на шинах составит
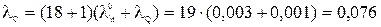 год
год  .
.
Надежность систем при постоянном раздельном резервировании
Схема замещения при постоянном раздельном резервировании помещена на рис. 5.10.
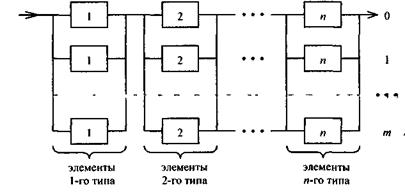
Рис. 5.10
Вероятность того, что произойдет отказ элементов i-го типа, равна произведению вероятностей отказов i-го элемента и всех элементов, его резервирующих, т.е.
 (5.31)
(5.31)
Вероятность безотказной работы i-го и всех резервирующих его элементов
 . (5.32)
. (5.32)
Если резервные и резервируемые элементы равнонадежны ( ), то
), то
 . (5.33)
. (5.33)
Поскольку функциональные группы элементов соединены последовательно, то вероятность безотказной работы в целом равна произведению вероятностей безотказной работы функциональных групп, т.е.
 . (5.34)
. (5.34)
Если все элементы равнонадежны,
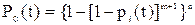 . (5.35)
. (5.35)
Пример 5.5
Система состоит из 10 последовательно включенных элементов. Вероятность безотказной работы каждого элемента для одного и того же момента времени
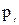 = 0,9. Сколько необходимо резервных элементов при постоянном резервировании обоими способами (общим и раздельным) для того, чтобы вероятность безотказной работы системы Рс = 0,95.
= 0,9. Сколько необходимо резервных элементов при постоянном резервировании обоими способами (общим и раздельным) для того, чтобы вероятность безотказной работы системы Рс = 0,95.
Решение
На основании формулы (5.26) можно записать соотношение
[1-p 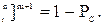 ].
].
Логарифмируя его, получаем
(m +1)lg(1- p  ) = lg(1- P
) = lg(1- P 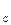 ).
).
Число резервных цепей (при n=10)
 .
.
Следовательно, для обеспечения требуемой надежности необходимо 6 резервных цепей по 10 элементов в каждой, т. е. всего 60 элементов.
Определим теперь необходимое число резервных элементов при раздельном резервировании, для чего представим формулу (5.35) в виде

После логарифмирования получаем

т.е. каждый основной элемент необходимо продублировать, а всего резервных элементов будет 10.
Таким образом, при раздельном резервировании в данном случае можно для той же надежности использовать в 6 раз меньше резервных элементов.
Надежность систем со смешанным соединением элементов
В принципе, оценка надежности систем со смешанным соединением элементов, т.е. с последовательно-параллельными связями, может осуществляться следующим образом. Если система состоит из n элементов, то, учитывая, что каждый элемент может находиться в двух состояниях (работоспособном или неработоспособном), система может пребывать в С = 2 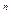 состояниях.
состояниях.
Все множество состояний системы разделяется на два подмножества: работоспособное и неработоспособное. Затем определяется вероятность пребывания системы в работоспособном состоянии, что и является конечной целью расчета.
Пример 5.6
 Определить вероятность безотказной работы в течение 4 лет системы, схема замещения которой по надежности представлена на рис. 5.11.
Определить вероятность безотказной работы в течение 4 лет системы, схема замещения которой по надежности представлена на рис. 5.11.
Интенсивность отказов всех элементов одинакова:

Рис. 5.11
Решение
Множество всех состояний системы С=2  =16, из которых 9 включают как минимум 2 находящихся в работоспособном состоянии элемента и образуют работоспособное подмножество. Таким образом, вероятность безотказной работы системы описывается многочленом
=16, из которых 9 включают как минимум 2 находящихся в работоспособном состоянии элемента и образуют работоспособное подмножество. Таким образом, вероятность безотказной работы системы описывается многочленом
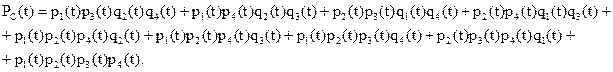
Вероятности безотказной работы и отказов i-го элемента в течение 4 лет рассчитываются соответственно как
 ;
;
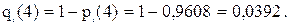
Вероятность безотказной работы системы в целом
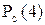 =4×0,9608
=4×0,9608  0,0392
0,0392  +4 0,9608
+4 0,9608  ×0,0392+0,9608
×0,0392+0,9608  =0,997.
=0,997.
Однако подобному подходу присущи значительные трудности, заключающиеся в том, что выделение работоспособных и неработоспособных состояний произвести не просто. Поэтому чаще используют метод свертки, состоящий в преобразовании исследуемых сложных систем со смешанным соединением элементов в более простые схемы, для которых имеются несложные аналитические выражения для расчета надежности.
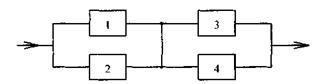
Предполагая, что восстановление отказавших элементов не производится, покажем применение метода свертки на следующем примере. Исходная схема представлена на рис. 5.12.

Рис. 5.12
Метод свертки состоит из нескольких этапов.
На первом этапе рассматриваются все параллельные соединения, которые заменяются эквивалентными элементами.
После первого этапа преобразований схема принимает вид, изображенный на рис. 5.13.

Рис. 5.13
Вероятности безотказной работы эквивалентных элементов в схеме на
рис. 5.13 определяются на основании формул (5.7), (5.8), (5.16):
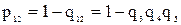 ;
; 
На втором этапе рассматриваются все последовательные соединения элементов, которые заменяются эквивалентными элементами. После второго этапа преобразований схема принимает вид, изображенный на рис. 5.14.

Рис. 5.14
Вероятности безотказной работы эквивалентных элементов в схеме на
рис. 5.14:
 ;
; 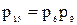 .
.
На третьем этапе вновь рассматриваются все параллельные соединения, которые заменяются эквивалентными элементами. Результат третьего этапа представлен на рис. 5.15.

Рис. 5.15
Вероятность безотказной работы эквивалентного элемента в схеме на рис. 5.15:
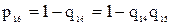 .
.
На четвертом этапе определяется вероятность безотказной работы всей системы:
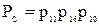 .
.
Метод свертки является весьма эффективным методом определения показателей надежности невосстанавливаемых последовательно-параллельных схем. Число элементов мало влияет на сложность проведения расчетов, в основном происходит увеличение числа этапов расчета.
Приближенный метод преобразования треугольника в звезду и обратно
На практике нередко встречаются системы, в которых схемы соединения элементов в надежностном смысле не могут быть сведены к последовательно-параллельным. Это системы, содержащие так называемые мостиковые схемы, т.е. системы, содержащие элементы типа треугольник и звезда. Такие схемы встречаются, например, в схемах электрических соединений подстанций и распределительных устройств.
Имеется ряд методов, позволяющих приближенно рассчитывать надежность таких систем. К ним относится метод преобразования треугольника в звезду и обратно. В этом случае в качестве показателей надежности используются вероятности отказов элементов. Выбор указанных характеристик объясняется тем, что метод преобразования треугольника в звезду и обратно является приближенным. Значение возникающей погрешности при оценке надежности системы зависит от вероятностей, характеризующих надежность элементов. Чем меньше эти вероятности, тем меньше погрешность оценки надежности системы. Так как обычно вероятности безотказной работы элементов близки к единице, то целесообразно использовать вероятности появления отказов.
Определим зависимости между вероятностями отказов элементов при преобразованиях, исходя из предположения, что характеристики надежности цепей, соединяющих одноименные точки в различных схемах, должны быть равны между собой.
Вначале рассмотрим точки 1 и 2 (рис. 5.16 и 5.17). Вероятности отказов для цепей при условии, что точка 3 присоединена к точке 2, будут равны: для звезды  , а для треугольника
, а для треугольника 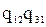 . Аналогично можно записать равенства и для двух других возможных вариантов соединения точек.
. Аналогично можно записать равенства и для двух других возможных вариантов соединения точек.
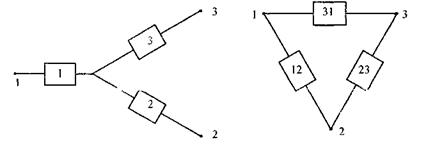
Рис. 5.16 Рис. 5.17
Таким образом, можно составить следующую систему уравнений:
 ;
;
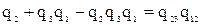 ; (5.36)
; (5.36)
 .
.
Считая, что вероятности отказов элементов малы, и пренебрегая произведениями  и
и  – вероятностями более высокого порядка малости, чем
– вероятностями более высокого порядка малости, чем 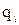 , получим следующие приближенные выражения:
, получим следующие приближенные выражения:
 ;
;  ;
;  . (5.37)
. (5.37)
Перемножим соответственно левые и правые части двух первых равенств системы (5.37) и разделим на третье равенство. Тогда
 . (5.38)
. (5.38)
Из (5.38) после сокращения одинаковых сомножителей имеем
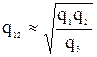 . (5.39)
. (5.39)
И аналогично получаем
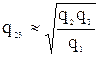 ;
;  . (5.40)
. (5.40)
Если предположить, что точка 3 в схеме звезды является свободной, то соответствующие вероятности появления отказов в схемах звезды и треугольника будут соответственно равны для звезды 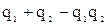 ;
;  ;
;  , а для треугольника
, а для треугольника  ;
; 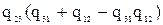 ;
;  .
.
Пренебрегая в этих выражениях величинами более высокого порядка малости, чем 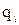 , (произведения
, (произведения  ), получим следующие приближенные зависимости:
), получим следующие приближенные зависимости:
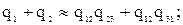
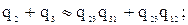 (5.41)
(5.41)
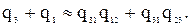
Прибавив к левой и правой частям первого уравнения в системе (5.41) соответственно левую и правую части третьего уравнения и вычтя соответственно левую и правую части второго уравнения, получим выражение  , которое было получено ранее (см. первое уравнение в системе (5.17)). Таким образом, приближенные формулы (5.37), (5.39), (5.40) могут быть использованы в процессе преобразования схемы треугольник в звезду и обратно.
, которое было получено ранее (см. первое уравнение в системе (5.17)). Таким образом, приближенные формулы (5.37), (5.39), (5.40) могут быть использованы в процессе преобразования схемы треугольник в звезду и обратно.
|
|
|


