Влияние изменения ограничений.

Зависимости максимального значения целевой функции (максимума числа комплектов конечной продукции) от изменения параметров ограничений    и   (каж­дого в  отдельности) непосредственно характеризуются значениями оптимальных оценок продукции и ресурсов. Пропорциональное изменение (увеличение или уменьшение) всех параметров ограни­чений не меняет значений оценок. При увеличении 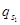  оценки ра­стут (до тех пор, пока существует решение задачи). При увеличе­нии  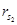 оценки снижаются (до нуля).

Возможности эквивалентной взаимозаменяемости конечной про­дукции и ресурсов в ограничениях модели определяются уравне­нием

(9)

Следует заметить, что количественные соотношения эквивалент­ной взаимозаменяемости, вытекающие из уравнения (9), справед­ливы только при таких значениях   и , которые не изме­няют значений оптимальных оценок.

Для того чтобы проанализировать влияние изменения ограни­чений на интенсивность применения различных производственных способов, осуществим упорядочение условий задачи.

Будем исходить из того, что для оптимального плана (п ₁ + m ₁) ограничений выполняются как равенства, а остальные (п – n ₁) + (т – m ₁) ограничений выполняются как строгие неравенства. Перенумеруем все исходные ограничения так, чтобы первые (п ₁ + m ₁) ограничений выполнялись как равенства, а остальные – как неравенства.

Выше мы пришли к выводу, что в оптимальном плане положи­тельными будут переменные (п ₁ + m ₁ – 1) производственных спо­собов и переменная . Изменим нумерацию переменных так, чтобы положительные переменные способов заняли первые места (век­тор X ₁ ), aза ними – переменная .

Тогда матрица модели может быть представлена в виде следую­щей блочной матрицы:

Введем новое обозначение для вектора ограничений: b = . Перенумеруем компоненты этого вектора в соответствии с новой нумерацией ограничений: b = .

Для оптимального плана справедливо уравнение:

,

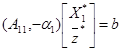откуда

(10)

Обозначим первые (п ₁ + m ₁ – 1) строк матрицы     через B₁₁, а последнюю строку – через β ₁₁. Тогда

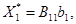(11)

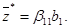(12)

Формулы (11) и (12) характеризуют зависимости оптималь­ных интенсивностей производственных способов и максимального числа комплектов от «жестких» ограничений задачи. Коэффици­енты матрицы B ₁₁ являются аналогами коэффициентов полных потребностей в продукции модели межотраслевого баланса. Од­нако эти коэффициенты могут иметь различные знаки, также как и коэффициенты вектора β ₁₁.

Из (11) и (12) выводятся формулы корректировки интенсив­ностей применяемых способов и числа комплектов конечной про­дукции при изменении ограничений:

(13)

(14)

Однако формулы (13) и (14) верны только при сохранении базиса оптимального плана задачи (набора векторов, соответст­вующих положительным переменным). Из линейного программи­рования известно, что базис оптимального плана не изменяется, пока переменные, вошедшие в оптимальный план, будут неотрица­тельны. Это означает, что в анализируемой модели условиями со­хранения базиса оптимального плана являются

(15)   или     (16)

(17)

Из этих условий находятся границы допустимых изменений каждой компоненты вектора b и области допустимых изменений одновременно нескольких компонент вектора b. Сохранение ба­зиса оптимального плана является также условием неизменности оптимальных оценок.

Включение в оптимальный план дополнительных производствен­ных  способов.

Как уже отмечалось, типичным свойством оптималь­ного плана модели является использование (п ₁+ т ₁ – 1) произ­водственных способов. Может оказаться, что большая часть имею­щихся производственных способов (из общего    числа N > n ₁ + т₁ – 1) не будет использоваться и преобладающая часть продукции будет производиться небольшим числом способов. Такая ситуация является нежелательной с точки зрения маневренности, надежности, адаптивности плана. В связи с этим интересно изучить, к каким последствиям приводит включение в оптимальный план дополнительных способов.

Эффективность производственных способов ψ измеряется оценками производственных способов:

. (18)

Для способов, вошедших в оптимальный план, Δ _ψ = 0. Для способов, не вошедших в оптимальный план, Δ _ψ  ≤ 0 (а в случае единственности оптимального плана Δ _ψ строго отрицательны). Оценки Δ _ψ показывают,  насколько уменьшится значение целевой функции при включении в оптимальный план ранее не входившего в него способа с единичной интенсивностью. Если же интенсивность вводимого способа равна x _ψ, то значение целевой функции умень­шится на Δ _ψ x _ψ.

Рассмотрим, как повлияет включение дополнительных способов (вектора Х₂) на интенсивности применения оптимальных (базис­ных) способов (вектор X₁. Добавив к вектору b ₁произведение – A₁₂ Х₂, получим на основе (11)

, 

откуда

(19)

Заметим также, что формула изменения максимального числа комплектов конечной продукции при включении вектора Х₂ имеет вид:

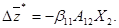(20)

Формулы (19) и (20) справедливы при сохранении базиса оптимального плана, т. е. при условиях

С помощью оценок способов (18) можно изучать целесообраз­ность включения в условия народнохозяйственной задачи новых способов. Новый способ φ будет эффективным (т. е. может войти в оптимальный план), если Δ _φ ≥ 0. Это условие может быть использовано для проектирования новых эффективных производст­венных способов.

Рассмотренные направления и методы анализа оптимального плана являются универсальными для всех линейных оптимиза­ционных моделей. Однако в более частных моделях экономико-математический анализ может выявлять и специфические свойства оптимальных решений.

12345

Поделиться:

Воспользуйтесь поиском по сайту: