Оптимизационные межотраслевые модели с производственными способами

Первый вариант модели (минимизация затрат труда на производство заданной конечной продукции).

Построим модель, представляющую собой непосредственное обобщение модели межотраслевого баланса, записанной в форме (22). В модели предусматривается возможность выбора между различными производственными способами. Пусть каждый вид продукции   производится несколькими способами , где T_j = {1,..., s_j }.При этом каждым способом выпускается только один продукт. Введем новые обозначения:

– объем производства продукции j способом _j;

– коэффициент пря­мых затрат продукции i на производство единицы продукции j способом _j;

– затраты труда на единицу продукции j, произ­водимой способом _j.

Модель имеет вид:

(32)

Модель (32) всегда имеет решение, если выполняются усло­вия, аналогичные условию продуктивности матрицы коэффициен­тов прямых материальных затрат модели межотраслевого баланса. Например, одно допустимое решение может быть получено, если включить в план по одному способу для каждого вида продукции, а все остальные переменные считать равными нулю. Так может быть составлено   систем уравнений межотраслевого баланса производства и распределения продукции, каждая из которых имеет решение, если матрица продуктивна.

Анализ модели позволяет выявить ряд ее интересных специфи­ческих свойств.

Теорема 1. При положительном векторе конечной про­дукции Y ⁰ > 0 производятся все продукты и каждый продукт про­изводится только одним способом.

Доказательство. Напомним, что мы исходим из пред­положения, что оптимальный план – единственный. Введем в ус­ловия дополнительные переменные Δ y_i (излишки конечной про­дукции сверх минимально необходимых объемов ), превращающие неравенства в равенства.

В каждом i -м уравнении

положительными являются только коэффициенты при переменных Х. Но поскольку все , то и все , т. е. оптимальном плане должны производиться все виды продуктов.

Максимальное число положительных переменных в оптимальном плане равно п (числу уравнений). Следовательно, в каждой сумме переменных   положительной может быть только одна переменная. Иначе говоря, в оптимальном плане каждый продукт про­изводится только одним способом.

Следствие. Из теоремы следует, что поскольку число воз­можных положительных переменных исчерпывается переменными способов производства, то все Δ y_i в оптимальном плане равны нулю. Иными словами, оптимальный план обращает исходные неравен­ства строго в равенства.

Введем дополнительные обозначения: X * – оптимальный план модели (каждая его компонента есть интенсивность применения какого-то «лучшего» способа производства); A *   – матрица коэффи­циентов материальных затрат, составленная из способов, которые вошли в оптимальный план.

Матрица А* аналогична матрице А межотраслевого баланса с той лишь разницей, что вместо средневзвешенных коэффициентов из разных способов в ней представлены коэффициенты только «луч­ших» способов. Матрицы A * и (Е – А*)обладают теми же экономико-математическими свойствами, что и матрицы межотраслевого ба­ланса. Среди этих свойств отметим, в частности, существование матрицы (Е – А*)^–1 ≥ 0. Элементы матрицы (Е – А*)^–1являются коэффициентами полных потребностей в выпуске продукции для получения единицы конечной продукции в оптимальном плане. Оптимальный план удовлетворяет следующей системе уравнений:

(E – A) X * = Y ⁰или X * = (E – A)^–1 Y ⁰.

Теорема 2. Базис оптимального плана, а следовательно, и выбор «лучших» способов остаются постоянными при любых из­менениях положительного вектора Y ⁰.

Доказательство. Для того чтобы базис оптимального плана оставался неизменным при переменном векторе Y ⁰, доста­точно – в соответствии с (15),– чтобы выполнялось условие

(E – A *)^–1 Y ⁰ ≥ 0.

Поскольку матрица (E – A *)^–1 ≥ 0, условие (E – A *)^–1 Y ⁰ ≥ 0 выполняется всегда при любом Y ⁰ ≥ 0 и тем более при Y ⁰ > 0.

Пусть для некоторого Y ⁰ > 0 получено решение X *. Базис по­лученного решения (Е – А*) остается неизменным и тогда, когда вектор Y ⁰ будет изменяться любым образом в положительной об­ласти (0 < Y ⁰ < +∞). Если базис оптимального плана – не­разложимая матрица, то теорема распространяется на случай Y ⁰ ≥ 0.

Это означает, что вычислив матрицу (E – A *)^–1для одного ва­рианта конечной продукции, можно неоднократно использовать ее для расчета производственной программы при других вариантах конечной продукции.

Из задачи, двойственной к (32), следует, что для способов, вошедших в оптимальный план , выполняются условия

Поэтому вектор оптимальных оценок продукции V * = (), характеризующих минимально необходимый прирост трудовых затрат в народном хозяйстве при увеличении конечной продукции, определяется решением системы уравнений

V* = V* A* + t*          или        V* = t* (A – V*)^–1.

Видим, что оптимальные оценки продукции в рассматриваемой модели равны коэффициентам полных трудовых затрат, исчислен­ным по лучшим производственным способам для каждого вида про­дукции.

Следствие. Оптимальные оценки 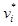  не изменяются при любых изменениях положительного вектора Y ⁰.

При неизменных коэффициентах производственных способов оптимальные оценки меняются только при изменении базиса оп­тимального плана. Теорема 2 доказывает, что в модели (32) базис оптимального плана остается постоянным при любых изменениях вектора Y ⁰ в положительной области, следовательно, не изме­няются и оптимальные оценки[1].

Постоянство оценок    облегчает их использование в различных планово-экономических расчетах, в частности, при корректировке вектора Y ⁰.

Второй вариант модели (максимизация конечной продукции в заданном ассортименте при ограниченных трудовых ресурсах).

Рассмотрим другую возможную постановку межотраслевой мо­дели с производственными способами: произвести максимальное число комплектов конечной продукции при ограниченных трудо­вых ресурсах: 

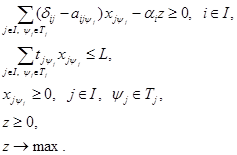(33)

Нетрудно установить, что модели (32) и (33) являются взаимным. В первой модели фиксируются   и минимизируются затраты труда, а во второй модели максимизи­руются z при фиксированном ресурсе труда. 

Отсюда следует, что если z ⁰ = max z или , то в

соответствии с теоремой взаимности оптимальные планы задач совпадают, трудовые ре­сурсы используются полностью, а оптимальные оценки продукции пропорциональны.  Сохраняются и все свойства оптимального плана и оптимальных оценок модели (32):

· в оптимальном плане производятся все продукты и каждый про­дукт производится только одним способом (для этого должно вы­полняться одно из условий: либо матрица способов неразло­жима, либо все );

· выбор лучших способов и оптимальные оценки не зависят от заданий по конечной продукции (ассортиментных коэффициентов);

· не производится «излишков» конечной продукции.

Отметим важное новое свойство: набор производственных спо­собов в оптимальном плане и значения оптимальных оценок не зависят от величины имеющегося ресурса. Действительно, по­скольку L есть единственная отличная от нуля компонента вектора ограничений задачи, то изменение L означает растяжение или сжа­тие вектора ограничений. Но такое преобразование не влияет на базис оптимального плана.

Вектор объемов производства выражается через матрицы ко­эффициентов полных затрат, сформированных из «лучших» спосо­бов:

Х = (Е – A *)^–1 α z = β * z, (34)

где β * = (Е – А*)^–1 α – вектор потребностей в выпуске продукции для получения одного комплекта конечной продукции.

Максимальное число комплектов z ^* находится из равенства t * (E – A *)^–1 α z = τ * z = L, откуда

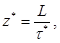(35)

где τ * = t * (Е – А*)^–1 α – полные трудовые затраты для получе­ния одного комплекта конечной продукции.

Подстановка (35) в (34) дает

  (36)

т. е. максимальное число комплектов и объемы производства прямо пропорциональны количеству имеющихся трудовых ресурсов. Оптимальная оценка трудовых ресурсов   является постоянной величиной.

В рассматриваемой модели условия максимизации конечной продукции могут быть сформулированы так же, как в моделях (1), (24), (27). С учетом данного уточнения приходим к модели:

(37)

Отмеченные выше свойства оптимального плана и оптимальных оценок полностью сохраняются. Однако решение задачи (37) су­ществует не всегда, так как наличных трудовых ресурсов может быть недостаточно для выполнения чрезмерно высоких заданий q_i.

Варианты модели с различными условиями максимизации конечной продукции.

Из теоремы 2 следует, что изменение объемов и структуры ко­нечной продукции (при сохранении Y ≥ 0) не оказывает никакого влияния на выбор лучших производственных способов. Это позво­ляет расчленить процесс оптимизационных расчетов и анализа оптимальных решений на три стадии:

· нахождение лучших производственных способов и минималь­ных затрат труда при заданном векторе конечной продукции на основе модели (32);

· определение объемов и структуры переменной части конечной продукции (можно использовать различные критерии и условия максимизации);

· расчет сбалансированного плана производства, обеспечиваю­щего выпуск всей конечной продукции при ограниченных трудовых ресурсах.

В качестве примера рассмотрим модель, включающую условия максимизации переменной части конечной продукции в виде ЦФП:

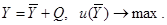
Решив задачу (32) с Y ⁰ = Q, определим матрицу А*, а также вектор оптимальных оценок продукции, равных коэффициентам полных затрат, исчисленным по лучшим производственным спосо­бам, V * = Т*, а также потребности в трудовых ресурсах для обес­печения постоянной части конечной продукции T * Q и остаток тру­довых ресурсов для выпуска переменной части конечной продукции .

На второй стадии решается задача максимизации ЦФП при ограниченных трудовых ресурсах:

(38)

Решение задачи (38) дает вектор .

Следует обратить внимание на интересный результат, характе­ризующий соотношения предельных полезных эффектов продукции и затрат труда на ее производство. В соответствии с условиями Куна – Таккера

(39)

Таким образом, в оптимальном плане рассматриваемой модели предельные полезные эффекты используемой конечной продукции пропорциональны общественно необходимым затратам труда на производство продукции. Оптимальные оценки продукции в модели (32) равны коэффициентам полных трудовых затрат, исчисленным по лучшим производственным способам, и являются постоянными величинами. Они оказывают влияние на выбор оп­тимальной структуры конечной продукции (вектора ); эта струк­тура «подбирается» так, чтобы отношения (39) выровнялись по всем используемым видам конечной продукции. Но выбор струк­туры конечной продукции не оказывает никакого влияния на зна­чения оптимальных оценок продукции.

На третьей стадии расчетов по модели находим вектор объемов производства ; он будет сбалансирован с имеющимися трудовыми ресурсами.

Аналогичным образом проводятся расчеты  по модели, вклю­чающей другие возможные критерии и условия максимизации ко­нечной продукции.

Таким образом, анализировавшиеся в данном параграфе опти­мизационные межотраслевые модели характеризуются двумя спе­цифическими свойствами.  Во-первых, в оптимальный план вклю­чается только по одному способу для каждого производимого вида продукции независимо от того, какое количество способов вводится в условия задачи. Во-вторых, объемы и структура используемой конечной продукции не оказывают никакого влияния на выбор производственных способов и определение общественно необходи­мых затрат на производство продукции.

Хотя выявленные свойства создают значительные удобства при проведении оптимизационных расчетов и анализе оптимальных решений, они не являются адекватным отражением свойств реаль­ной экономики. Данные свойства моделей обусловлены тем, что выбор производственных способов осуществляется с позиций наи­более эффективного использования только одного ограниченного ресурса – труда. Решения, получаемые с помощью рассматривае­мых моделей, должны интерпретироваться как условно-оптималь­ные, т. е. получаемые в предположении, что трудовые ресурсы яв­ляются единственным дефицитным ресурсом в народном хозяйстве. Эти условно-оптимальные решения должны затем корректироваться с учетом использования других ограниченных ресурсов.

12345

Поделиться:

Воспользуйтесь поиском по сайту: