Оптимизационные модели на основе матрицы межотраслевого баланса

Общая линейная оптимизационная модель построена на основе матрицы таких производственных способов, что каждый из них мо­жет выпускать несколько видов продукции, каждый вид продукции  может выпускаться несколькими способами.

Далее мы рассмотрим более частные оптимизационные модели, сохраняющие некоторые специфические допущения модели межотраслевого баланса: сначала – модели, в которых каждый способ выпускает только один продукт и каждый продукт выпускается только одним способом, а затем – модели, в ко­торых сохраняется только первое из указанных допущений. Такая последовательность анализа моделей выбрана для того, чтобы «перекинуть  мост» между моделями межотраслевого баланса и оптимизационными моделями народного хозяйства и проследить изменение свойств решений (сбалансированных и оптимальных) при изменении предпосылок модели и включении в нее новых ус­ловий.

Модель межотраслевого баланса как частный случай оптимизационных моделей

Оптимизационные модели по сравнению с балансовыми пред­ставляют собой более совершенный тип моделей социалистической экономики. Однако было бы неправильно противопоставлять их друг другу. Во-первых, основные условия балансовых моделей обязательно включаются в оптимизационные модели. Во-вторых, балансовые модели могут интерпретироваться и исследоваться как частный случай оптимизационных моделей.

Попытаемся сформулировать модель межотраслевого баланса на языке оптимизационных задач. Рассмотрим систему уравнений межотраслевого баланса производства и распределения продукции совместно с ограничением по трудовым ресурсам производствен­ной сферы:

(21)

Основная задача плановых расчетов с помощью этой модели состоит в том, чтобы при заданном векторе Y ⁰ = () и имеющихся трудовых ресурсах L найти вектор необходимых объемов произ­водства X = (x_j). Покажем, что эту задачу можно представить в виде задачи линейного программирования:

  (22)

Эта задача отличается от (21) только тем, что допускается полу­чение конечной продукции сверх заданных минимальных объемов, а затраты трудовых ресурсов минимизируются. Очевидно, что ре­альным экономическим условиям отвечают только такие решения X * = (x *), при которых .

Задаче (22) соответствует двойственная задача, с помощью которой находятся оптимальные оценки продукции :

(23)

Оптимальный план X * задачи (22) характеризуется следую­щими свойствами:

· он единственный;

· если Y ⁰ > 0 (или Y ⁰ ≥ 0 и А – неразложимая матрица), то Х* > 0;

· балансы производства и распределения продукции выполняются строго как равенства, т. е. излишки конечной продукции не про­изводятся;

· оптимальный план X * не зависит от коэффициентов целевой функции t_J ≥ 0.                                                                       

На рис. 1 видно, что оптимальный план всегда является вер­шиной «клюва» при любых допустимых наклонах целевой функции. Обе задачи (и прямая, и двойственная) всегда имеют единственное решение, если матрица А продуктивна и Y ⁰ ≥ 0. При этом реше­ние прямой оптимизационной задачи сводится к решению системы уравнений   и поэтому оно не зависит от значений коэффициентов минимизируемой функции. Решение двойственной задачи находится из системы урав­нений   ипоэтому оно не зависит от коэффициентов минимизируемой функции. При этом оптимальные оценки продук­ции равны коэффициентам полных трудовых затрат.

Равенство функционалов прямой и двойственной задачи 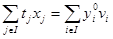  имеет место при любых положительных значениях t_j и 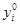. Оно означает, что суммарная оценка всей конечной продукции равна сумме трудовых затрат в народном хозяйстве.