 |
Поиск решения задачи с параметрами.
|
|
|
|
Задания высокого уровня сложности с развернутым ответом №18
В действующем формате ЕГЭ задания 18 (задания С5) содержат параметры и предполагают исследование свойств различных элементарных функций. Поэтому подготовку к их решению, очевидно, следует начать с краткого обзора основных методов решения задач с параметрами. Эти методы демонстрируются на соответствующих примерах, которые также можно рассматривать как тренировочные.
Общая постановка задачи с параметром.
Для определенности, рассмотрим задачу с параметром на примере уравнения, поскольку общая ее постановка не зависит от конкретного вида задачи.
Пусть дано уравнение 
(1) с двумя переменными 
и 
.
Задача с параметром в данном случае формулируется следующим образом: для каждого значения параметра из некоторого числового множества 
решить уравнение (1) относительно переменной , т.е. привести его к виду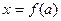 
(2).
Множество называется областью изменения параметра и в общем случае (если нет дополнительных условий) считается множеством действительных чисел 
.
Таким образом, уравнение (1) можно рассматривать как бесконечное множество (семейство) уравнений относительно , каждое из которых получается при подстановке в это уравнение любого конкретного значения параметра 
.
Решить уравнение с параметром – это значит, разбить множество всех значений параметра на подмножества, на каждом из которых выражение 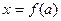имеет различный вид и найти его, если оно существует.
Те значения, которые осуществляют такое разбиение области изменения параметра, называются контрольными. При этих значениях или при переходе через них происходят качественные изменения семейства уравнений. Способы их нахождения определяются конкретными условиями задачи.
|
|
|
Возможно также, что уравнению (1) удовлетворяет конечный набор пар 
, которые находятся непосредственно из его решения. Однако и в этом случае переменную принято считать параметром и исходя из этого, формулировать ответ задачи.
Еще раз следует отметить, что сформулированные выше положения распространяется и на неравенства, и на системы уравнений и неравенств с параметрами.
Основные методы решения задач с параметрами.
Поиск решения задачи с параметрами.
В данном разделе рассматриваются задачи, решением которых в определенном смысле "управляют" параметр или неизвестная величина . В этом случае выбор контрольных значений и разбиение области изменения на подмножества очевидны и решение сводится к перебору различных случаев зависимости от значений переменных или .
- Для каждого значения параметра решить неравенство
Решение.
Перепишем неравенство в виде 
.
Это неравенство равносильно следующей системе неравенств
.
Ее решением «управляет» параметр . Необходимо последовательно рассмотреть три случая: 
; 
и 
. Получаем совокупность следующих трех систем неравенств:
Решим систему (1):
Система не имеет решений, т.к.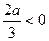 
.
Решим систему (3):
.
Ответ: при неравенство не имеет решений; при 
;
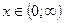при 
.
- Решение относительно параметра.
(использование параметра как равноправной переменной).
Метод решения относительно параметра используется, прежде всего, в том случае, когда степень искомой переменной в уравнении или неравенстве выше двух, а степень параметра не превосходит двух. Также он используется и тогда, когда для решения задачи необходимо менять местами переменные и параметры.
2. Для каждого значения параметра a решить уравнение
Решение. Так как данное уравнение является квадратным относительно , то представим его в следующем виде: 
.
|
|
|
Найдем дискриминант этого квадратного уравнения: 
Следовательно, 
. Отсюда, 
или 
.
Отметим, что 
при 
. Этот корень существует при 
.
Решим полученную совокупность квадратных уравнений
или 
.
; 
при 
; 
при 
.
Очевидно, что 
при 
, 
при 
.
Ответ: при 
уравнение не имеет корней; при уравнение имеет один корень: 
; при 
уравнение имеет два корня: 
; при уравнение имеет три корня: 
;
при 
уравнение имеет четыре корня: ; 
;
при уравнение имеет три корня: 
, 
, 
.
Полученные результаты можно проиллюстрировать графически, изобразив на плоскости (x,a) параболы и , а также прямые 
.
3. 
На плоскости (x,y) указать все точки, через которые не проходит ни одна из кривых семейства 
.
Решение. Ни одна из кривых указанного семейства не проходит через точку плоскости (x,y) тогда и только тогда, когда не существует тройки чисел 
, удовлетворяющих уравнению 
. Это возможно тогда и только тогда, когда 
. Ответ: 
.
- Найти все значения параметра
, при которых уравнение 
имеет три различных корня.
Решение. Так как данное уравнение является квадратным относительно , то представим его в следующем виде: 
.
Найдем дискриминант этого квадратного уравнения: 
 |
Ответ: -9; -5; 0; 4.
5. Найдите все значения , при каждом из которых уравнение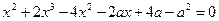 
имеет не менее трех корней. Найдите все корни, которые получаются при единственном значении параметра .
Решение. Преобразуем уравнение к виду 
. Корни этого уравнения 
. На плоскости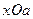 
уравнение задает совокупность двух парабол. Найдем их общие точки: 
; 
; 
. Таким образом, общие точки этих парабол: 
и 
. Координаты вершин парабол: 
и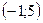 
.
Уравнение имеет три и более корней при 
. Каждый корень получается при двух различных значениях , кроме корней 
и 
. Корень получается при единственном значении 
, так как прямая пересекает график в единственной точке . Аналогично, корень получается при единственном значении 
.
Ответ: , при , при .
- Симметрия и четность.
Одним из наиболее общих методов решения задач с параметром является поиск необходимых условий. Он состоит в том, что сначала формируется множество значений параметра, которые могут удовлетворять условию задачи, а затем из этого множества находится собственно решение. В данном разделе рассмотрим этот метод на примере использования симметрии аналитических выражений.
|
|
|
Характеристическим признаком ряда задач является присутствие в них неизвестных в качестве аргументов четных функций. Таким образом, при замене на 
условия задачи не меняются, т.е. геометрические образы этих аналитических выражений симметричны относительно оси ординат. Возможна также симметрия относительно прямых 
или 
. В этих случаях условия не меняются соответственно при переменах местами и 
; и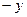 
. Как правило, в таких задачах требуется найти значения параметров, при которых существует единственное решение или нечетное число решений.
- Определить, при каких значениях параметра a система имеет единственное решение, и найти его:
Решение.
; 
.
Таким образом, исходная система может быть представлена в следующем виде:
.
Очевидно, что если 
- решение этой системы, то и 
также является ее решением. Следовательно, для существования единственного решения необходимо, чтобы 
. При имеем: 
.
Решения второго уравнения системы: 
.
Решение 
существует только при 
. Проверим, является ли оно единственным решением системы 
.
При 
; 
. Таким образом, первое уравнение имеет два решения: 
и . Второму уравнению удовлетворяет только .
При 
система имеет вид 
.
, 
. 
- единственное решение.
При 
система имеет вид 
.
- уравнение, а значит и система, не имеет решения.
Ответ: при система имеет единственное решение ; при - единственное решение .
- Найдите все значения параметра , при которых система уравнений
имеет ровно три решения.
Решение.
Если 
- решение системы, то и 
- решение системы. Значит, необходимым условием существования нечетного числа решений является равенство 
или 
.
Подставляя эти значения в исходную систему, и учитывая, что 
, получаем систему 
.
Система может иметь нечетное число решений при 
Выясним, когда система имеет ровно три решения:
Очевидно, что из четырех окружностей с центрами, соответственно, в точках 
, 
, 
и 
только три имеют по три общих точки с множеством точек, заданных уравнением 
.
|
|
|
Ответ: -4; 4; 6.
|
|
|
