 |
Координатная плоскость. Построение параметрического семейства кривых (метод сечений).
|
|
|
|
Предположим, что уравнение или неравенство, содержащее параметр, приведено к виду 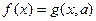 или
или 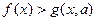
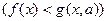 . Тогда уравнение
. Тогда уравнение 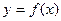 определяет на координатной плоскости
определяет на координатной плоскости 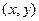 некоторую кривую, а уравнение
некоторую кривую, а уравнение 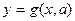 - семейство кривых, в котором каждому допустимому значению параметра
- семейство кривых, в котором каждому допустимому значению параметра  соответствует одна кривая. При этом в зависимости от значений параметра
соответствует одна кривая. При этом в зависимости от значений параметра  кривые семейства
кривые семейства 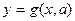 могут занимать различные положения относительно кривой
могут занимать различные положения относительно кривой 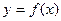 . Графическое исследование сечения кривой
. Графическое исследование сечения кривой 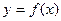 семейством кривых
семейством кривых 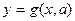 позволяет найти дальнейшее правильное аналитическое решение исходного уравнения или неравенства.
позволяет найти дальнейшее правильное аналитическое решение исходного уравнения или неравенства.
8. Найти все значения параметра  , при которых неравенство
, при которых неравенство 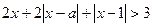 выполняется при всех действительных значениях
выполняется при всех действительных значениях  .
.
Решение.
Перенесем слагаемые, не содержащие параметр, в правую часть неравенства: 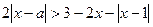 .
.
Построим график функции 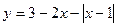 и найдем те значения
и найдем те значения  , при которых все точки графиков параметрического семейства функций
, при которых все точки графиков параметрического семейства функций 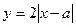 лежат выше этого графика.
лежат выше этого графика. 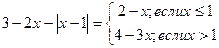 ;
; 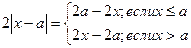 .
.
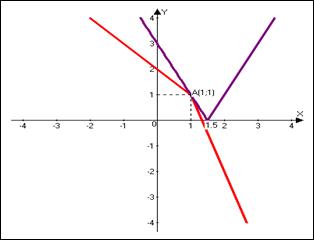 Очевидно, что контрольным значением параметра является значение параметра
Очевидно, что контрольным значением параметра является значение параметра 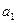 , при котором график функции
, при котором график функции 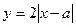 проходит через точку
проходит через точку 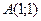 . Подставим ее координаты в уравнение
. Подставим ее координаты в уравнение 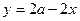 , получим:
, получим: 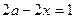 ;
; 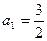 . Ответ:
. Ответ:  .
.
9. Найти все значения параметра  , при которых неравенство
, при которых неравенство 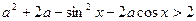 выполняется при всех действительных значениях
выполняется при всех действительных значениях  .
.
Решение. Представим неравенство как квадратное относительно 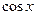 и сделаем замену
и сделаем замену  . Получим следующую систему неравенств:
. Получим следующую систему неравенств:
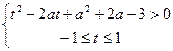
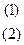 .
.
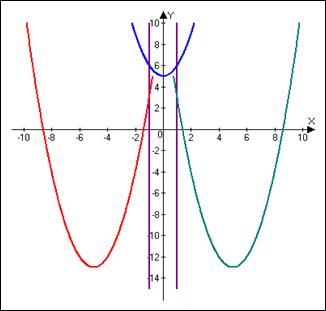 Абсцисса вершины квадратного трехчлена
Абсцисса вершины квадратного трехчлена  зависит от параметра:
зависит от параметра: 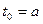 .
.
Семейство парабол разделим на три группы. К первой отнесем те из них, вершины которых расположены левее промежутка 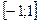 ; ко второй – вершины которых расположены внутри или на границе промежутка
; ко второй – вершины которых расположены внутри или на границе промежутка 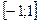 ; к третьей - вершины которых расположены правее этого промежутка.
; к третьей - вершины которых расположены правее этого промежутка.
Необходимым и достаточным условием положительности функции в указанном промежутке является выполнение неравенства 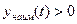 при
при  . Для первой группы – это неравенство
. Для первой группы – это неравенство 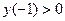 , для второй -
, для второй - 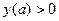 , для третьей -
, для третьей - 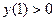 . Таким образом, получим совокупность трех систем неравенств:
. Таким образом, получим совокупность трех систем неравенств:
|
|
|
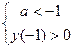 (1),
(1), 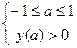 (2),
(2), 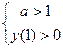 (3).
(3).
Решим последовательно каждую из них.
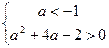 (1),
(1), 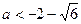 .
.
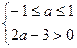 (2). Система несовместна.
(2). Система несовместна.
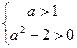 (3),
(3), 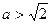 . Ответ:
. Ответ: 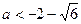 ,
, 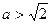 .
.
10. Найдите все значения  , при каждом из которых система
, при каждом из которых система 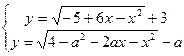 имеет единственное решение.
имеет единственное решение.
Решение
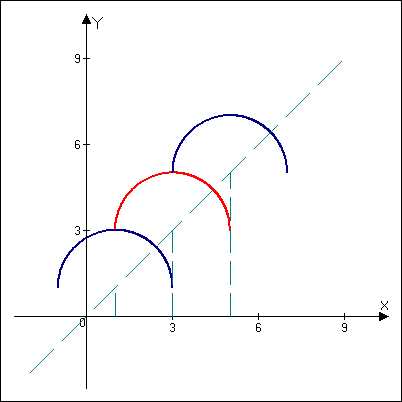
Система имеет единственное решение тогда и только тогда, когда графики функций 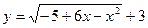 и
и 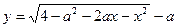 имеют единственную общую точку.
имеют единственную общую точку.
Первое уравнение запишем в виде 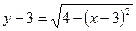

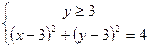 . Это система задает верхнюю полуокружность с центром
. Это система задает верхнюю полуокружность с центром 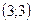 и радиусом 2. Второе уравнение запишем в виде
и радиусом 2. Второе уравнение запишем в виде 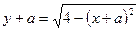

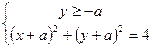 . Это система задает верхнюю полуокружность с центром
. Это система задает верхнюю полуокружность с центром  и радиусом 2.
и радиусом 2.
При 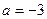 полуокружности совпадают.
полуокружности совпадают.
При  ,
, 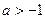 полуокружности не имеют общих точек.
полуокружности не имеют общих точек.
При 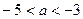 ,
, 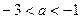 полуокружности имеют единственную общую точку.
полуокружности имеют единственную общую точку.
Ответ: 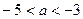 ,
, 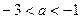 .
.
11. Найти все значения параметра  , при каждом из которых система неравенств
, при каждом из которых система неравенств 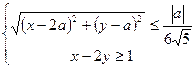 имеет решения.
имеет решения.
Решение
Первое неравенство задает на координатной плоскости круг радиуса 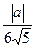 с центром в точке
с центром в точке 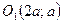 . Второе неравенство задает полуплоскость с границей
. Второе неравенство задает полуплоскость с границей 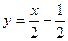 . Очевидно, что центр круга при всех значениях
. Очевидно, что центр круга при всех значениях  лежит вне заданной полуплоскости, т.к.
лежит вне заданной полуплоскости, т.к.  .
.
Система имеет решения, если круг и полуплоскость имеют общие точки, т.е. если радиус окружности не меньше расстояния от точки 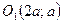 до прямой
до прямой  . Расстояние от точки
. Расстояние от точки  до прямой
до прямой 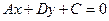 находится по формуле
находится по формуле  . Отсюда
. Отсюда 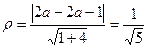 ;
;  ;
; 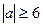 .
.

Не используя данную формулу, можно было потребовать, чтобы радиус был не меньше расстояния между параллельными прямыми  и
и 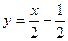 .
.
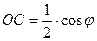 ;
; 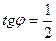 ;
; 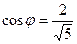 ;
;  . Далее аналогично.
. Далее аналогично.
Ответ: 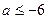 ;
;  .
.
12. (ЕГЭ 2011). Найдите все положительные значения  , при каждом из которых система
, при каждом из которых система 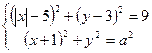 имеет единственное решение.
имеет единственное решение.
Решение
Если 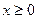 , то уравнение
, то уравнение 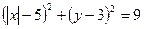 задаёт окружность
задаёт окружность 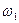 с центром в точке
с центром в точке 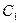
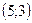 радиуса 3, а если
радиуса 3, а если 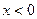 , то оно задаёт окружность
, то оно задаёт окружность  с центром в точке
с центром в точке 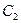
 радиуса 3.
радиуса 3.
При положительных значениях параметра  уравнение
уравнение  задаёт окружность
задаёт окружность 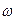 с центром в точке
с центром в точке 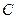
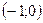 радиуса
радиуса  . Поэтому задача состоит в том, чтобы найти все значения
. Поэтому задача состоит в том, чтобы найти все значения  , при каждом из которых окружность
, при каждом из которых окружность 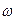 имеет единственную общую точку с объединением окружностей
имеет единственную общую точку с объединением окружностей 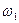 и
и  .
.
|
|
|
Из точки 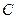 проведем луч
проведем луч 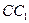 и обозначим
и обозначим 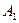 и
и 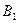 точки его пересечения с окружностью
точки его пересечения с окружностью 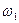 , где
, где 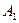 лежит между
лежит между 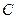 и
и 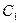 . Так как
. Так как 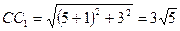 , то
, то 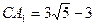 ,
, 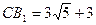 .
.
При 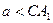 или
или 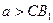 окружности
окружности 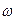 и
и 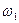 не пересекаются.
не пересекаются.
При  окружности
окружности 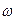 и
и 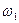 имеют две общие точки.
имеют две общие точки.
При  или
или 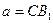 окружности
окружности 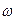 и
и 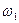 касаются.
касаются.
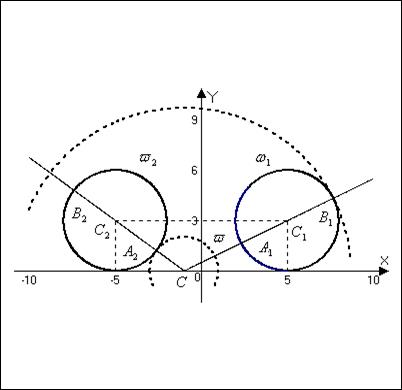
Из точки 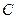 проведем луч
проведем луч 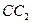 и обозначим
и обозначим 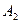 и
и 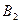 точки его пересечения с окружностью
точки его пересечения с окружностью  , где
, где 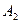 лежит между
лежит между 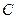 и
и 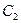 . Так как
. Так как 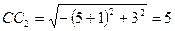 , то
, то 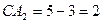 ,
, 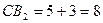 .
.
При 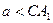 или
или 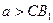 окружности
окружности 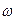 и
и  не пересекаются.
не пересекаются.
При  окружности
окружности 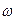 и
и  имеют две общие точки.
имеют две общие точки.
При  или
или 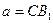 окружности
окружности 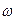 и
и  касаются.
касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность 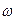 касается ровно с одной из окружностей
касается ровно с одной из окружностей 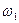 и
и  и не пересекается с другой.
и не пересекается с другой.
Ответ: 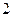 ;
; 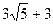 .
.
13. (ЕГЭ 2011). Найдите все значения  , при каждом из которых система
, при каждом из которых система 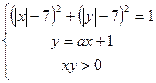 имеет единственное решение.
имеет единственное решение.
Решение
Первое уравнение при условии 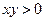 задает на плоскости две единичные окружности с центрами
задает на плоскости две единичные окружности с центрами 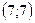 и
и 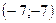 , а второе – прямую
, а второе – прямую 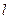 с угловым коэффициентом
с угловым коэффициентом  , проходящую через точку
, проходящую через точку 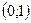 .
.
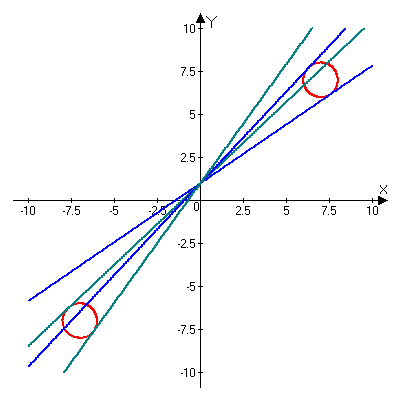
Прямая 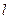 касается окружности с центром в точке
касается окружности с центром в точке 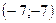 единичного радиуса тогда и только тогда, когда система
единичного радиуса тогда и только тогда, когда система 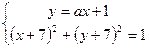
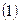 имеет единственное решение. Для этого необходимо, чтобы квадратное уравнение
имеет единственное решение. Для этого необходимо, чтобы квадратное уравнение 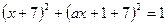 имело единственное решение. Приведем уравнение к виду
имело единственное решение. Приведем уравнение к виду 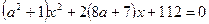 и из равенства нулю дискриминанта получим:
и из равенства нулю дискриминанта получим: 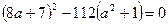 , откуда
, откуда 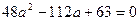 . Значит,
. Значит, 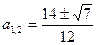 и система
и система 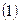 имеет решения только при
имеет решения только при 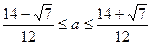 .
.
Аналогично, прямая 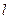 касается окружности с центром в точке
касается окружности с центром в точке 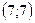 единичного радиуса тогда и только тогда, когда система
единичного радиуса тогда и только тогда, когда система 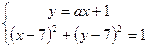
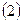 имеет единственное решение. Для этого необходимо, чтобы квадратное уравнение
имеет единственное решение. Для этого необходимо, чтобы квадратное уравнение  имело единственное решение. Приведем уравнение к виду
имело единственное решение. Приведем уравнение к виду  и из равенства нулю дискриминанта получим:
и из равенства нулю дискриминанта получим: 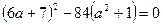 , откуда
, откуда 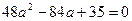 . Значит,
. Значит,  и система
и система 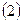 имеет решения только при
имеет решения только при 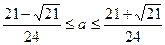 .
.
Так как 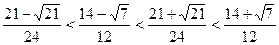 , то исходная система имеет единственное решение при
, то исходная система имеет единственное решение при 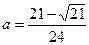 и при
и при 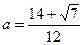 .
.
Ответ:  ;
; 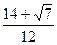 .
.
- Найдите все положительные значения параметра
 , при каждом из которых система
, при каждом из которых система  имеет ровно два решения.
имеет ровно два решения.
Решение
Выражаем из второго уравнения  и подставляем в первое, получаем следующую систему:
и подставляем в первое, получаем следующую систему: 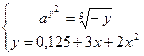 . Решим уравнение
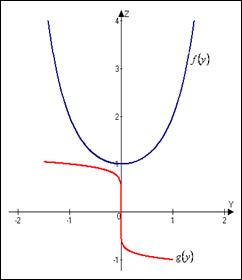
. Решим уравнение 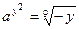 . Рассмотрим взаимное расположение графиков функций
. Рассмотрим взаимное расположение графиков функций  и
и 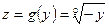 в следующих трех случаях:
в следующих трех случаях:
|
|
|

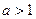
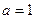
 Итак, при
Итак, при 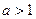 графики функций
графики функций 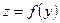 и
и
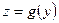 общих точек не имеют и, следовательно, уравнение
общих точек не имеют и, следовательно, уравнение 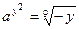 не имеет корней.
не имеет корней.
При 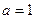 графики пересекаются в точке с абсциссой
графики пересекаются в точке с абсциссой 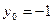 и уравнение
и уравнение 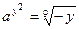 имеет один корень
имеет один корень 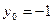 .
.
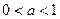
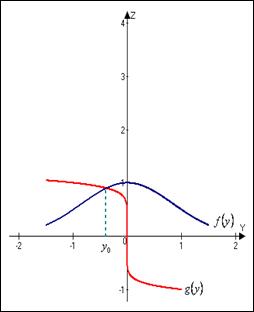
При 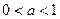 графики пересекаются в точке с абсциссой
графики пересекаются в точке с абсциссой 
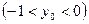 и уравнение
и уравнение 
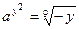 имеет один корень
имеет один корень 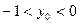 .
.
Подставим  во второе уравнение системы:
во второе уравнение системы:  .
. 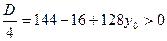 ;
; 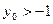 .
.
Ответ: 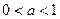
4.2. Координатно – параметрическая плоскость. Метод областей.
При графическом исследовании задач с параметрами наряду с координатной плоскостью 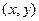 целесообразно также использовать координатно – параметрическую плоскость
целесообразно также использовать координатно – параметрическую плоскость 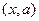 . Если возможно построить на координатно – параметрической плоскости множество всех точек, координаты которых
. Если возможно построить на координатно – параметрической плоскости множество всех точек, координаты которых  и
и  удовлетворяют условию задачи, то затем нетрудно поставить в соответствие каждому значению параметра
удовлетворяют условию задачи, то затем нетрудно поставить в соответствие каждому значению параметра  этого множества значение соответствующей координаты
этого множества значение соответствующей координаты  . Это и будет решением задачи. Следует также указать те значения параметра, при которых задача не имеет решения. Выбор контрольных значений параметра определяется конкретным видом построенных множеств.
. Это и будет решением задачи. Следует также указать те значения параметра, при которых задача не имеет решения. Выбор контрольных значений параметра определяется конкретным видом построенных множеств.
15. (ЕГЭ 2011). Найдите все значения  , при каждом из которых система
, при каждом из которых система 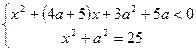 имеет решения.
имеет решения.
Решение
Разложим левую часть неравенства на множители 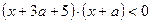 . Это неравенство задаёт пару вертикальных углов плоскости
. Это неравенство задаёт пару вертикальных углов плоскости 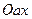 . Уравнение задаёт окружность с центром
. Уравнение задаёт окружность с центром  радиуса 5.
радиуса 5.
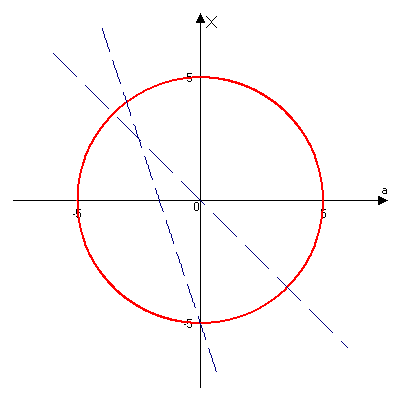
Решения системы – точки дуг окружности, лежащие в указанных вертикальных углах. Абсциссы концов этих дуг находим из систем
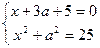 и
и 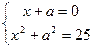
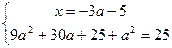
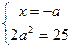
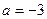 ;
;  .
. 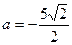 ;
; 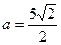 .
.
Ответ: 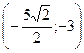 ;
; 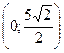 .
.
16. Найдите все значения параметра  , при котором уравнение
, при котором уравнение  имеет нечетное число различных корней.
имеет нечетное число различных корней.
Решение
Разложим левую часть уравнения на множители:
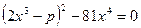 ;
; 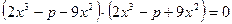 .
.
Таким образом, получили следующую совокупность двух уравнений:
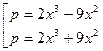 .
.
На плоскости 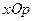 построим графики функций
построим графики функций
 и
и 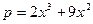
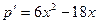
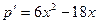
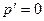
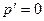
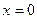 - точка максимума
- точка максимума  - точка максимума
- точка максимума
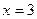 -точка минимума
-точка минимума 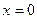 - точка минимума
- точка минимума
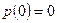 ;
; 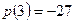 .
. 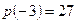 ;
; 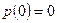 .
.

Ответ: -27; 0; 27.
17. Найдите все значения  , при каждом из которых общие решения неравенств
, при каждом из которых общие решения неравенств  и
и 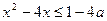 образуют на числовой оси отрезок длины единица.
образуют на числовой оси отрезок длины единица.
Решение.
Представим данные неравенства в виде следующей системы: 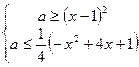 .
.
|
|
|
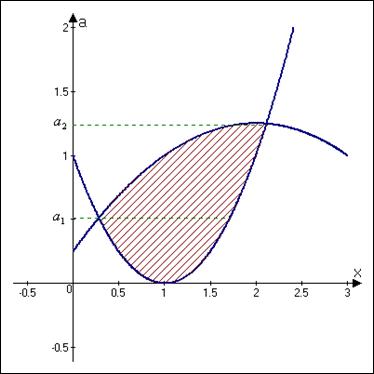
На плоскости  решением этой системы являются точки, лежащие не ниже параболы
решением этой системы являются точки, лежащие не ниже параболы  и не выше параболы
и не выше параболы 
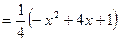 .
.
Найдем точки пересечения этих парабол:
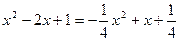 ;
;
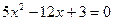 ;
; 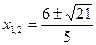 ;
; 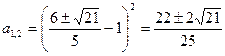 .
.
Отметим, что так как 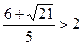 , то точка пересечения парабол с координатами
, то точка пересечения парабол с координатами 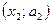 лежит правее вершины параболы
лежит правее вершины параболы 
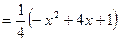 , координаты которой
, координаты которой 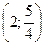 .
.
Решим относительно  уравнения
уравнения
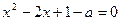 и
и 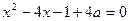
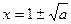 ;
;  .
.
Таким образом, следует рассмотреть три системы:
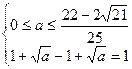
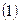 ;
; 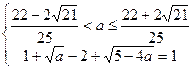
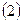 ;
; 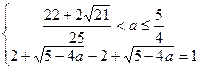
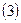
Решение системы 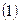 :
: 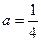 ; системы
; системы 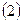 :
: 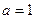 .
.
Система 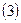 несовместна, так как решение второго уравнения системы
несовместна, так как решение второго уравнения системы 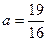
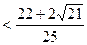 .
.
Ответ: 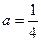 ;
; 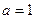 .
.
|
|
|


