 |
Функциональный подход к решению уравнений и неравенств.
|
|
|
|
Для решения уравнений и неравенств, содержащих различные типы элементарных функций, достаточно часто приходится использовать общие методы исследования свойств функций, такие как область определения и множество значений, четность, монотонность, экстремумы и т.д.
18. Найти все значения 
, при которых уравнение 
имеет хотя бы один корень.
Решение. Рассмотрим уравнение 
, где 
. Здесь 
- кусочно-линейная функция, графиком которой является ломаная линия, имеющая своими звеньями отрезки прямых и два луча.
Любое звено этой ломаной при 
- часть некоторой прямой с угловым коэффициентом 
Для 
любое из звеньев имеет угловой коэффициент 
Отсюда следует возрастание при и ее убывание при . Таким образом, 
.
Условие существования корня данного уравнения имеет вид: 
. 
, 
, 
, 
. Ответ: .
19. Найти все значения параметра , при которых неравенство 
выполняется для любого значения 
.
Решение.
Найдем область изменения функции, стоящей под знаком модуля. 
, где 
- дополнительный аргумент.
.
Таким образом, получаем следующую систему
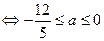. Ответ: 
.
20. (ЕГЭ 2012). Найдите все значения параметра , при каждом из которых неравенство 
выполняется для всех 
.
Решение. Рассмотрим функцию 
= 
.
Эта функция возрастает на промежутке 
и убывает на промежутке 
.
; 
.
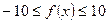Отрезок 
не должен лежать на участке монотонности, иначе 
.
Следовательно, 
; 
.
Наибольшее значение 
достигается либо при 
, либо при 
.
Наименьшее значение достигается при 
. Итак, имеем систему: 
Ответ: 
.
21. (ЕГЭ 2013). Найдите все значения параметра , при каждом из которых уравнение 
имеет хотя бы один корень.
Решение. Рассмотрим две функции: 
и 
. Так как 
, то 
.
Функция является кусочно-линейной.
При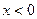 
угловой коэффициент либо 4, либо 12.,
|
|
|
при 
угловой коэффициент либо -4, либо -12.
Значит, 
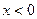возрастает при и убывает при , поэтому 
.
Исходное уравнение имеет хотя бы один корень тогда и только тогда, когда 
.
или 
Ответ: -5; 
;.
22. (ЕГЭ 2012). 
Найдите все значения параметра , при каждом из которых уравнение 
имеет более трех различных решений.
Решение. Перепишем уравнение в виде 
или
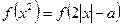, где 
.
, следовательно, 
- монотонно возрастающая функция.
.
; 
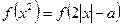
- два решения при 
;
- два решения при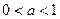 
, отличных от решений первого уравнения.
Ответ: .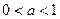
.
23. Найдите все значения параметра , при каждом из которых уравнение 
не имеет действительных решений.
Решение. Обозначим 
, 
, тогда 
.
В результате указанной замены исходное уравнение примет следующий вид:
.
Введем функцию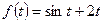 
и запишем уравнение в виде 
или с учетом нечетности : 
Так как 
, то -монотонно возрастающая функции, то
.
Отсюда имеем 
;
; 
; 
.
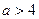24. Найдите наибольшее целое значение , при котором уравнение 
имеет ровно два различных решения.
Решение
Преобразуем правую часть уравнения по формуле 
.
Получим 
.
Левую часть уравнения преобразуем следующим образом:
.
Обозначим 
; 
, тогда уравнение примет вид: 
или 
Введем функцию 
.
Так как 
, то -монотонно возрастающая функция.
Следовательно,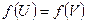 
.
Отсюда имеем 
; 
; 
; 
.
Ответ: 
.
25. Найти все значения параметра , при каждом из которых уравнение 
имеет по крайней мере два корня, один из которых неотрицателен, а другой не превосходит
-1.
Решение. Найдем ОДЗ:
.
.
Ответ: 
; 
; 
.
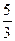26. При каких значениях параметра неравенство 
справедливо для всех значений из отрезка 
?
Решение. Обозначим 
, тогда неравенство будет иметь вид 
; 
;
- монотонно возрастающая функция;
; 
; 
.
Ответ; 
.
27. (ЕГЭ 2014). Найдите все значения параметра , при которых для любого действительного выполнено неравенство 
Решение. Пусть 
, тогда неравенство запишется в виде 
. Поскольку 
, нам требуется найти все значения , при которых неравенство выполнено при 
.
|
|
|
Рассмотрим функции 
и 
. Функция - кусочно-линейная. Угловой коэффициент ее звеньев не превосходит 10. Функция 
- линейная функция с угловым коэффициентом 11. Значит, функция 
возрастающая. Свое наименьшее значение на промежутке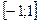 
она принимает при 
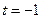. Таким образом, если неравенство 
выполнено при 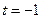, то оно выполняется и при 
.
При 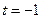неравенство принимает вид 
; 
. 
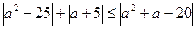при 
.
.
Таким образом, при ; 
.
Ответ: 
; 
.
28. (ЕГЭ 2014). Найдите все значения параметра , при которых уравнение 
имеет ровно два решения.
Решение. Пусть 
, тогда уравнение имеет вид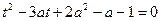 
; 
.
; 
; 
.
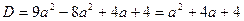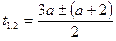При решений нет.
ОДЗ: 
; 
; 
.
.
- монотонно убывающая функция.
При 
; 
.
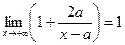Таким образом, при выражение 
принимает по одному разу все значения из промежутка 
.
При 
; .
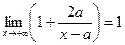При выражение принимает по одному разу все значения из промежутка 
. При 
имеем одно решение 
.
; 
; 
.
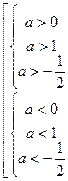Ответ: 
; 
; .
| Содержание критерия | Баллы |
| Обоснованно получен правильный ответ | |
С помощью верного рассуждения получено множество значений , отличающееся от искомого только включением точек  и/или 
| |
С помощью верного рассуждения получен один из промежутков множества : или ; возможно, с включением граничных точек и/или исключением точки 
| |
| Верно найдена хотя бы одна из граничных точек множества значений или ; ИЛИ получено хотя бы одно из уравнений
| |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
29. Найдите все значения , при каждом из которых уравнение 
имеет ровно два различных корня.
Решение. Пусть 
, 
.
Если 
, тогда 
, 
и 
.
Если 
, тогда 
; 
.
Обозначим 
.
Исходное уравнение имеет ровно два корня тогда и только тогда, когда уравнение 
имеет единственный корень, больший 1, или два корня, один из которых больше 1, а другой меньше 1.
Уравнение имеет единственный корень, если его дискриминант равен нулю: 
; 
; 
или 
.
При уравнение 
имеет единственный корень . В этом случае исходное уравнение имеет единственный корень .
При уравнение 
имеет единственный корень 
. В этом случае исходное уравнение имеет два корня.
Графиком функции является парабола, ветви которой направлены вверх. Для того, чтобы уравнение имело два корня, один из которых больше 1, а другой меньше 1, необходимо и достаточно, чтобы выполнялось неравенство 
; 
; 
; 
.
|
|
|
Ответ: -170; (-2; 5).
30. Найти все значения параметра , при каждом из которых множество значений функции 
содержит отрезок 
.
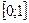Решение. Перепишем заданную функцию так: 
.
Для того, чтобы множество значений функции содержало отрезок 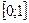, необходимо, чтобы уравнения 
(1) и 
(2) имели корни, т.е. нашлись такие значения переменной , при которых выполняются равенства (1) и (2). Тогда в силу свойства функции, непрерывной на некотором отрезке, функция будет принимать все промежуточные значения между 0 и 1.
Рассмотрим уравнение (1): 
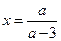
Таким образом, уравнение (1) имеет решение при любых значениях , кроме 
.
Рассмотрим уравнение (2):
.
; 
; 
.
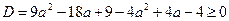Ответ: 
.
31. (ЕГЭ – 04.06.15). Найдите все значения , при каждом из которых система уравнений 
имеет более двух решений.
Решение.
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если 
, то уравнение имеет вид
; 
; 
.
Полученное уравнение задает окружность с центром 
и радиусом 5.
2) Если 
, то уравнение имеет вид
; 
; 
.
Полученное уравнение задает окружность с центром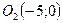 
и радиусом 5.
Полученные окружности пересекаются в точках 
и 
, лежащих на прямой 
. Найдем эти точки: 
; 
; 
; 
.
Таким образом, искомое множество состоит из двух дуг 
и 
с концами в точках 
и 
.
Второе уравнение системы задает семейство параллельных прямых 
с угловым коэффициентом 
. Заметим, что эти прямые перпендикулярны прямой 
и прямая 
принадлежит этому семейству (при 
).
Найдем, при каких значениях параметра прямые проходят соответственно через точки и , то есть система имеет три решения:
; 
. 
.
Найдем, при каких значениях прямые касаются дуг и .
Следовательно, дуги и имеют общие касательные. Прямые касаются дуг и при 
, то есть при этих значениях параметра система имеет два решения.
Ответ: 
; 
.
32. (ЕГЭ – 27.09.15). Найдите все значения , при каждом из которых система 
имеет единственное решение.
Решение. Запишем первое уравнение в следующем виде 
; 
.
|
|
|
; 
.
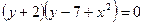При уравнение 
принимает вид 
, откуда при 
получаем 
. С учетом условия 
получаем, что при 
и 
решений нет, а при 
имеется одно решение.
При уравнение принимает вид
; 
.
Дискриминант данного квадратного уравнения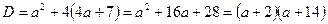 
.
Таким образом, уравнение не имеет решений при 
, имеет единственное решение при 
и при 
, имеет два решения при 
и при 
. При 
.
Таким образом, при 
корни уравнения больше 2, поскольку 
, а минимум квадратичной функции 
достигается при 
; при 
корни уравнения не превосходят 2, поскольку 
, а минимум квадратичной функции достигается при 
; при 
только один из двух корней уравнения не превосходит 2, поскольку 
.
Определим значения , при которых возможны совпадения решений из двух разобранных выше случаев. Имеем: 
, откуда 
или 
. Случай не рассматривается, поскольку . Значит, 
.
Таким образом, исходная система не имеет решений при 
, имеет единственное решение при ; 
; и , имеет два решения при 
; 
и 
.
Ответ: ; ; ; .
| Содержание критерия | Баллы |
| Обоснованно получен правильный ответ | |
С помощью верного рассуждения получено множество значений , отличающееся от искомого только включением /исключением точек ,  ,  и/или
| |
С помощью верного рассуждения получен один из промежутков множества :  или ; возможно, с включением граничных точек
| |
| Верно найдено хотя бы одно из значений : , или ; или получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
| |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
|
|
|
