 |
Расчет длины тормозного пути
|
|
|
|
| v 1, км/ч | v 2, км/ч | v ср, км/ч | φкр | b т, Н/т | 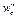 , Н/т , Н/т
| r ср, Н/т | Si , м | Σ Si , м |
| 0,105 | 490,4 | 23,7 | -464,1 | 116,7 | 116,7 | |||
| 0,112 | 523,0 | 21,0 | -490,4 | 92,8 | 209,5 | |||
| 0,120 | 560,4 | 18,7 | -529,1 | 70,9 | 280,4 | |||
| 0,133 | 621,1 | 16,7 | -587,8 | 49,6 | 330,0 | |||
| 0,150 | 700,5 | 15,0 | -665,5 | 31,3 | 361,3 | |||
| 0,177 | 826,6 | 13,7 | -790,3 | 15,8 | 377,1 | |||
| 0,227 | 1060,1 | 12,7 | -1022,8 | 4,1 | 381,2 |
Пример 7. Определить наибольшую скорость, с которой поезд из примера 6 должен двигаться, чтобы при экстренном торможении остановиться на расстоянии не более 600 метров.
Решение. Допустим, что путь подготовки тормозов зависит только от скорости движения и изменяется линейно. Тогда найдем две точки, которые определяют эту прямую. Первая точка соответствует скорости v = 0. При этом путь подготовки тормозов 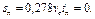
Вторую точку возьмем для скорости v = 100 км/ч:
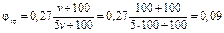 ;
;
 с;
с;
 м.
м.
Проводим по двум точкам линию 1 на рисунке 8.
Затем из точки на оси абсцисс, соответствующей расстоянию 600 м, в обратном направлении последовательно от v = 0 до пересечения с линией 1 строим кривую скорости 2, соответствующую режиму экстренного торможения. Построение можно выполнить графическим методом Липеца либо по результатам аналитического, либо численного интегрирования уравнения движения поезда. Точка A пересечения линий 1 и 2 соответствует началу отсчета действительного тормозного пути s д и скорости начала торможения  км/ч.
км/ч.
Таким образом, если рассмотренный выше поезд на спуске крутизной 5 ‰ начнет экстренное торможение при скорости  км/ч, то, пройдя путь подготовки тормозов
км/ч, то, пройдя путь подготовки тормозов 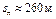 и действительный тормозной путь
и действительный тормозной путь  он остановится на расстоянии 600 м от места поворота ручки крана машиниста в тормозное положение. При скорости начала торможения большей, чем скорость в точке A на рисунке 8, тормозной путь будет больше 600 м.
он остановится на расстоянии 600 м от места поворота ручки крана машиниста в тормозное положение. При скорости начала торможения большей, чем скорость в точке A на рисунке 8, тормозной путь будет больше 600 м.
|
|
|

Рисунок 8 – Определение предельно допустимой по тормозам скорости движения поезда
На практике часто требуется для любого спуска на рассматриваемом участке определить предельно допустимое значение скорости движения поезда, при котором длина тормозного пути не превысит некоторое заданное значение. Иначе говоря, требуется определить ограничение скорости по тормозным средствам для любого из спусков на рассматриваемом участке. В этом случае обычно решают задачу, аналогичную рассмотренной в примере 7, но для трех (двух) значений уклона. В качестве этих уклонов можно принять прямой горизонтальный участок пути (i = 0), наибольший спуск и средний по величине уклона спуск. По полученным трем значениям скорости строят графическую зависимость v доп(i). Пользуясь этой графической зависимостью, находят ограничение допустимой скорости движения поезда по тормозам для любого, встречающегося на рассматриваемом участке спуска.
Пример 8. Определить ограничение скорости движения поезда по тормозам на участке, где наибольший спуск i = –12 ‰. Длина тормозного пути 1200 м. Масса состава Q = 4450 т. В составе 52 четырехосных вагона. Тормозные колодки стандартные чугунные. Диаграмма удельных замедляющих сил для режима экстренного торможения приведена на рисунке 9.
Решение. Количество осей в составе
 осей.
осей.
Значение расчетного тормозного коэффициента при K р= 70 кН/ось
 .
.

Рисунок 9 – Графическое определение предельно допустимых по тормозам
значений скорости движения поезда
Рассчитаем длину пути подготовки тормозов для уклонов 0 ‰, – 6 ‰ и – 12 ‰. Принимая для v = 100 км/ч  (см. пример 7), время подготовки тормозов определим по формуле (38):
(см. пример 7), время подготовки тормозов определим по формуле (38):
для i = 0
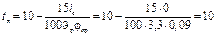 с;
с;
для i = – 6 ‰
 c;
c;
для i = – 12 ‰
 c.
c.
Значения пути подготовки тормозов по формуле (36):
для i = 0
|
|
|
 м;
м;
для i = – 6 ‰
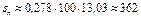 м;
м;
для i = – 12 ‰
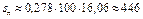 м.
м.
Эти значения отложим по горизонтали на уровне, соответствующем скорости v = 100 км/ч. Соединим полученные точки с началом координат, построив тем самым линии, по которым изменяется значение sп в зависимости от скорости начала торможения для трех значений уклонов. Из точки, соответствующей заданному значению тормозного пути (s = 1200 м), в обратном направлении строим кривые скорости для режима экстренного торможения на уклонах i, равных 0, –6, –12 ‰. Точки пересечения линий, соответствующих одинаковым уклонам и дают значения предельно допустимой скорости движения для этих уклонов. Так для i = 0 ‰ vд = 97 км/ч, для i = – 6 ‰ vд = 88 км/ч и для i = – 12 ‰ vд = 80 км/ч. Используя полученные значения, строим зависимость vд (i), по которой для любого спуска от i = 0 ‰ до i = – 12 ‰ можно определить ограничение скорости движения поезда по тормозным средствам.
Выше рассмотрены примеры тормозных задач, в условии которых задана обеспеченность поезда тормозами. Задачи второй группы, подразумевающие определение необходимых тормозных средств решают, сводя их к задачам первой группы, что рассмотрим на примере.
Пример 9. Определить достаточно ли тормозных средств у поезда для реализации скорости 80 км/ч на спуске i = –10 ‰ при длине тормозного пути s т = 1200 м. Масса локомотива P = 276 т, состава Q = 4300 т. Все вагоны четырехосные на роликовых подшипниках. Средняя осевая нагрузка вагонов q o = 17 т/ось, все оси тормозные, а тормозное нажатие K р = 70 кН/ось.
Решение. Задаемся четырьмя значениями расчетного тормозного коэффициента Jр1 = 2; Jр2 = 3; Jр3 = 4; Jр4 = 5. Для каждого из принятых значений Jр находим удельные замедляющие силы в зависимости от скорости движения поезда и результаты вычислений сводим в таблицу 10.
Далее решение задачи сводится к четырехкратному решению тормозной задачи первой группы. Для каждого из принятых четырех значений Jр решают задачу, аналогичную рассмотренной в примере 7. Результаты вычислений и графических построений, выполняемых при решении, приведены в таблице 11 и на рисунке 10.
Значение t п рассчитываем по формуле (38), поскольку число осей в заданном составе 

Рисунок 10 – Графическое определение необходимой обеспеченности поезда тормозами
|
|
|
Таблица 10
|
|
|


