 |
Определение коэффициентов регрессии
|
|
|
|
Кафедра металлургической технологии
Расчетно-пояснительная записка по дисциплинам
«Математическое моделирование и оптимизация металлургических
процессов»
«Вычислительная техника в инженерных расчетах»
Оптимизация химического состава сплава
Студент: Бородин А.Н.
Группа: 321 – ОМД
Преподаватель: Грузман В.М.
Преподаватель: Баранов Ю.М.
1998г.
Содержание
| Введение | 4 | |
| Глава 1 | Верхний, нижний и основной уровень. Расчет интервала варьирования | 5 |
| Глава 2 | Расчет уравнений | 7 |
| Расчет уравнения для C, Si и σ текучести | 7 | |
| Расчет уравнения для С, Si, относительного удлинения | 11 | |
| Расчет уравнения для С, Si, предела прочности | 13 | |
| Глава 3 | Проверка уравнений | 17 |
| Глава 4 | Оптимизация состава сплава | 18 |
Целью нашей работы является нахождение оптимального состава стали М74 для получения наилучших физических свойств сплава: предела текучести, предела прочности, абсолютного удлинения. В данной работе использован метод линейного программирования и дальнейшая оптимизация по двухфакторной модели, что позволило получить одновременно решение графическим методом и на ЭВМ.
В ходе работы был определен наилучший состав стали по заданным требованиям:
- для получения минимального предела текучести содержание углерода и кремния должно быть следующим: C=0,7%; Si=0,4%;
- для получения максимального предела прочности: C=0,8%; Si=0,25%;
- для получения максимального абсолютного удлинения: C=0,7%; Si=0,4%.
|
|
|
ВВЕДЕНИЕ
Математическая модель является эффективным современным средством управления производством. В современных условиях быстроизменяющейся обстановке во всех сферах металлургического производства, от исходных материалов до готовой продукции, когда необходимо быстро и с минимальной ошибкой принимать ответственные решения, необходимо знание основ математического моделирования, уметь не только пользоваться готовыми моделями, но и принимать участие в их создании.
Линейное программирование - один из самых распространенных методов решения оптимизационных задач на практике. Он является частью математического программирования вообще, направленного на решение задач о распределении дефицитных ресурсов с учетом технологических, экономических и других ограничений, накладываемых условиями функционирования реального моделируемого объекта. Для линейного программирования используют линейные математические зависимости. Рождение метода линейного программирования связано с именами фон Неймана, Хичкока, Стиглера, которые использования положения теории линейных неравенств и выпуклых множеств, сформулированные в прошлом веке, для оказания помощи руководителям в принятии оптимальных решений. Основная задача линейного программирования была сформулирована в 1947 году Георгом Данцигом из управления ВВС США, который высказал гипотезу, что к анализу взаимосвязей между различными сторонами деятельности крупного предприятия можно подходить с позиций линейного программирования, и что оптимизация программы может быть достигнута максимизацией (минимизацией) линейной целевой функции.
В металлургической технологии наибольшее распространение получила задача составления технологических смесей, а конкретно, задача оптимизации химического состава сплавов.
Для того, чтобы исследовать метод «Оптимизации химического состава сплава», я воспользовался данными из прокатного цеха НТМК, которые отражают влияние содержания углерода и кремния в стали М74 на ее физические свойства: предел текучести, предел прочности и абсолютное удлинение. Данные взяты в ЦЛК (см. приложение 2).
|
|
|
ГЛАВА 1
ОПРЕДЕЛЕНИЕ ВЕРХНЕГО, НИЖНЕГО И ОСНОВНОГО УРОВНЯ. РАСЧЕТ ИНТЕРВАЛА ВАРЬИРОВАНИЯ
По данным выборки назначим верхний и нижний уровень варьирования факторов и рассчитаем интервал варьирования и средний (основной, нулевой) уровень.
Для этого построим таблицу, отражающую частоту «попадания» каждого числа:
Таблица 1
Подсчет частот
| Х1 | К1 | Х2 | К2 |
| 0,71 | 7 | 0,25 | 2 |
| 0,72 | 26 | 0,26 | 5 |
| 0,73 | 50 | 0,27 | 0 |
| 0,74 | 49 | 0,28 | 6 |
| 0,75 | 79 | 0,29 | 11 |
| 0,76 | 35 | 0,30 | 21 |
| 0,77 | 53 | 0,31 | 38 |
| 0,78 | 48 | 0,32 | 88 |
| 0,79 | 36 | 0,33 | 66 |
| 0,8 | 9 | 0,34 | 44 |
| 0,81 | 4 | 0,35 | 28 |
| 0,82 | 4 | 0,36 | 42 |
| 0,37 | 29 | ||
| 0,38 | 7 | ||
| 0,39 | 13 | ||
| Итого | 400 | 400 |
Таблица 2
Нижний, верхний, основной уровень и интервал варьирования
| Факторы | Х1 | Х2 |
| Нижний уровень | 0,71 –0,74 | 0,25 – 0,29 |
| Верхний уровень | 0,80 – 0,83 | 0,37 – 0,41 |
| Основной уровень | 0,77 | 0,32 |
| Интервал варьирования | 0,04 | 0,05 |
Для нахождения среднего уровня выполняем следующие расчеты:
Найдем средние значения каждого интервала и основной уровень.


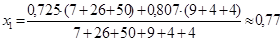 основной уровень
основной уровень


основной уровень х2=  0
0
ГЛАВА 2
РАСЧЕТ УРАВНЕНИЙ
Необходимо рассчитать три уравнения:
- уравнение для C, Si и σ текучести,
- уравнение для C, Si и относительного удлинения,
- уравнение для C, Si и σ прочности.
2.1. Расчет уравнения для C, Si и σ текучести
Для того, чтобы оценить влияние факторов, часто имеющих разную размерность, производится кодирование – факторы делаем безразмерными, кроме этого кодирование обеспечивает легкость обработки данных. 
 , где хi - кодированная переменная.
, где хi - кодированная переменная.
2.1.1.Составление матрицы планирования
Таблица 3
Матрица планирования
| N | X1 | Х2 | y1 | 
| x1x2 |
| 1 | 1 | 1 | 667(40) | 667 | 1 |
| 2 | 1 | -1 | 589(20) | 608,5 | -1 |
| 628(357) | |||||
| 3 | -1 | 1 | 647(45) | 603,5 | -1 |
| 589(12) | |||||
| 589(191) | |||||
| 589(310) | |||||
| 4 | -1 | -1 | 598(19) | 586,4 | 1 |
| 598(134) | |||||
| 540(165) | |||||
| 598(253) | |||||
| 598(372) |
Определение коэффициентов регрессии
|
|
|
 ,
,
где N - число опытов по матрице планирования.
b0 =(667+603,5+586,4+608,5)/4=616,35
b1 =(667+608,5-603,5-586,4)/4=21,4
b2 =(667-608,5+603,5-586,4)/4=18,9
b3 =(667-608,5-603,5+586,4)/4=10,35
|
|
|


