Проверка значимости коэффициентов при факторах

Дисперсия воспроизводимости служит для оценки ошибки опыта, для этого необходимо найти опыты в центре плана, для чего составим табл.4.

Таблица 4

Опыты в центре плана.

N	X1	x2	y1
3	0,77	0,32	589
96			598
118			589
138			598
215			598	594.4
237			589
257			598
334			598
356			589
376			598

,

где m – число опытов

Проверка значимости коэффициентов регрессии.

;

;

;

;

        

t_табл. = 2,26; т.е. все коэффициенты значимы.

       Получили уравнение

Проверка адекватности математической модели

Проверяем адекватность математической модели по критерию Фишера. Для получения адекватности необходимо, чтобы разброс в точке и разброс в регрессии был сопоставим. ,

где f =N-(k+1)=4-(3+1)=0

Y₁=616,35+21,4+18,9+10,35=667

Y₂=616,35+21,4-18,9-10,35=608,5

Y₃=616,35-21,4+18,9-10,35=603,5

Y₄=616,35-21,4-18,9+10,35=586,5

Критерий Фишера

                             

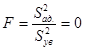
Математическая модель адекватна.

 

Переход от кодированных переменных к натуральным

2.2. Расчет уравнения для С, Si, относительного удлинения         

2.2.1. Составление матрицы планирования

Таблица 5

Матрица планирования

N	x1	x2	x1x2	y2
1	1	1	1	6,7(40)	6,7
2	1	-1	-1	5(20)	5,5
				6(357)
3	-1	1	-1	7,3(45)	9,85
				10,7(12)
				10,7(191)
				10,7(310)
4	-1	-1	1	6(19)	6,2
				6(134)
				7(165)
				6(253)
				6(372)

Расчет дисперсии воспроизводимости

Таблица 6

Опыты в центре плана

N	x1	x2	y2
3	0,77	0,32	7,3	6,1
96			5,3
118			7,3
138			5,3
215			5,3
237			7,3
257			5,3
334			5,3
356			7,3
376			5,3

Определение коэффициентов регрессии

b₀ =(6,7+5,5+9,85+6,2)/4=7,0625

b₁ =(6,7+5,5-9,85-6,2)/4=-0,9625

b₂ =(6,7-5,5+9,85-6,2)/4=1,2125

b₃ =(6,7-5,5-9,85+6,2)/4=-0,6125

Проверка значимости коэффициентов регрессии

;

;

;

;

t_табл. = 2,26; t3< t_табл., t2< t_табл., т.е. эти коэффициенты незначимы.

Проверка адекватности математической модели

Y₁=7,0625+1,2125=8,275

Y₂=7,0625-1,2125=5,85

Y₃=7,0625+1,2125=8,275

Y₄=7,0625-1,2125=5,85

Критерий Фишера: ; F_расч. <F_табл.

Математическая модель адекватна.

Переход от кодированных переменных к натуральным

 

Расчет уравнения для С, Si, предела прочности

2.3.1. Составление матрицы планирования

Таблица 7

Матрица планирования

N	x1	x2	x1x2	Y3
1	1	1	1	1079	1079
2	1	-1	-1	1030	1044,5
				1059
3	-1	1	-1	1028	1024,5
				1010
				1040
				1020
4	-1	-1	1	1020	1028
				1030
				1010
				1040
				1040

                       

Вычисление дисперсии воспроизводимости

Таблица 8

Опыты в центре плана

N	X1	x2	y2
3	0,77	0,32	1010	1006,5
96			1010
118			1030
138			1001
215			991
237			1001
257			991
334			1010
356			1001
376			1020

 

Определение коэффициентов регрессии

b₀ =(1079+1044,5+1024,6+1028)/4=1044

b₁ =(1079+1044,5-1024,6-1028)/4=17,75

b₂ =(1079-1044,5+1024,6-1028)/4=7,75

b₃ =(1079-1044,5-1024,6+1028)/4=9,5

Проверка значимости коэффициентов регрессии

;

;

;

;

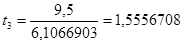
t_табл. = 2,26; t3< t_табл., t2< t_табл., т.е. эти коэффициенты незначимы.

Проверка адекватности математической модели

Y₁=1044+17,75=1061,75

Y₂=1044+17,75=1061,75

Y₃=1044-17,75=1026,25

Y₄=1044-17,75=1026,25

  

Критерий Фишера: ; F_расч. <F_табл.

Математическая модель адекватна.

 

Переход от кодированных переменных к натуральным

ГЛАВА 3

ПРОВЕРКА УРАВНЕНИЙ

       Проверим составленные уравнения, отражающие влияние содержания углерода и кремния в стали на ее физические свойства.

Таблица 9

Проверка уравнений

N опыта	295	392	149
x1=	0,75	0,73	0,79
x2=	0,39	0,29	0,33
yпр1.=	687	589	589
yрасч1.=	632,69	604,61	643,81
yпр.2=	10,7	6	6
yрасч.2=	8,76	6,335	7,305
yпр.3=	1059	1030	1001
yрасч.3=	1035,1125	1026,2375	1052,8625

ГЛАВА 4

ОПТИМИЗАЦИЯ СОСТАВА СПЛАВА

       Необходимо оптимизировать химический состав сплава по C и Si. В ходе работы были выявлены зависимости механических свойств от состава сплава:

σ_тек. – предел текучести,

абсолютное удлинение,

σ_пр. – предел прочности;

σ_тек. =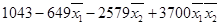

σ_пр.=

 

Оптимальный состав сплава по пределу текучести

 Найти оптимальный состав сплава по пределу текучести, т.е. найти такой состав сплава, который обеспечит минимальный предел текучести при следующих ограничениях:

 ГОСТ – 84182-80

Строим график(рис.1).

σ_тек.      min

Координаты:       

σ_пр.:

Координаты: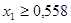       

Оптимальный состав сплава при σ_тек.      min является C=0,7%; Si=0,4%.

σ_тек.=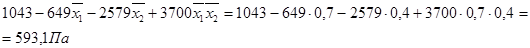

Рис. 2. Нахождение минимума предела текучести

 

Оптимальный состав сплава по абсолютному удлинению

Найти оптимальный состав сплава по абсолютному удлинению, т.е. найти такой состав сплава, который обеспечит максимальное абсолютное удлинение при следующих ограничениях:

, ГОСТ – 84182-80

 

Строим график(рис.2).

σ_тек.

max

Координаты:       

σ_пр.:

Координаты: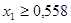       

Оптимальный состав сплава при _.          max является C=0,7%; Si=0,4%.

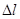
Рис. 3. Нахождение максимального абсолютного удлинения.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: