 |
Метацентры и метацентрические радиусы
|
|
|
|
Глава 5
Начальная остойчивость судна
Общее понятие об остойчивости
Остойчивостью называется способность судна противодействовать силам, отклоняющим его от положения равновесия, и возвращаться в первоначальное положение равновесия после прекращения действия этих сил.
Полученные в главе 4 «Плавучесть» условия равновесия судна не являются достаточными для того, чтобы оно постоянно плавало в заданном положении относительно поверхности воды. Необходимо еще, чтобы равновесие судна было устойчивым. Свойство, которое в механике именуется устойчивостью равновесия, в теории судна принято называть остойчивостью. Таким образом, плавучесть обеспечивает условия положения равновесия судна с заданной посадкой, а остойчивость – сохранение этого положения.
Остойчивость судна меняется с увеличением угла наклонения и при некотором его значении полностью утрачивается. Поэтому представляется целесообразным исследование остойчивости судна на малых (теоретически бесконечно малых) отклонениях от положения равновесия с Θ = 0, Ψ = 0, а затем уже определять характеристики его остойчивости, их допустимые пределы при больших наклонениях.
Принято различать остойчивость судна при малых углах наклонения (начальную остойчивость) и остойчивость на больших углах наклонения.
При рассмотрении малых наклонений имеется возможность принять ряд допущений, позволяющих изучить начальную остойчивость судна в рамках линейной теории и получить простые математические зависимости ее характеристик. Остойчивость судна на больших углах наклонения изучается по уточненной нелинейной теории. Естественно, что свойство остойчивости судна единое и принятое разделение носит чисто методический характер.
|
|
|
При изучении остойчивости судна рассматривают его наклонения в двух взаимно перпендикулярных плоскостях – поперечной и продольной. При наклонениях судна в поперечной плоскости, определяемых углами крена, изучают его поперечную остойчивость; при наклонениях в продольной плоскости, определяемых углами дифферента, изучают его продольную остойчивость.
Если наклонение судна происходит без значительных угловых ускорений (перекачивание жидких грузов, медленное поступление воды в отсек), то остойчивость называют статической.
В ряде случаев наклоняющие судно силы действуют внезапно, вызывая значительные угловые ускорения (шквал ветра, накат волны и т.п.). В таких случаях рассматривают динамическую остойчивость.
Остойчивость - очень важное мореходное свойство судна; вместе с плавучестью оно обеспечивает плавание судна в заданном положении относительно поверхности воды, необходимом для обеспечения хода и маневра. Уменьшение остойчивости судна может вызвать аварийный крен и дифферент, а полная потеря остойчивости - его опрокидывание.
Чтобы не допустить опасного уменьшения остойчивости судна все члены экипажа обязаны:
- всегда иметь четкое представление об остойчивости судна;
- знать причины, уменьшающие остойчивость;
- знать и уметь применять все средства и меры по поддержанию и восстановлению остойчивости.
Равнообъемные наклонения судна. Теорема Эйлера
Остойчивость судна изучается при так называемых равнообъемных наклонениях, при которых величина подводного объема остается неизменной, а меняется лишь форма подводной части судна.
Введем основные определения, связанные с наклонениями судна:
- ось наклонения – линия пересечения плоскостей двух ватерлиний;
- плоскость наклонения – перпендикулярная оси наклонения плоскость, проходящая через ЦВ, соответствующий исходному положению равновесия судна.;
|
|
|
- угол наклонения – угол поворота судна около оси наклонения (угол между плоскостями ватерлиний), измеряемый в плоскости наклонения;
-
 |
равнообъемные ватерлинии – ватерлинии, отсекающие при наклонениях судна равные по величине клиновидные объемы, один из которых при наклонении судна входит в воду, а другой выходит из воды.
Рис. 33. К рассмотрению теоремы Эйлера
При известной исходной ватерлинии для построения равнообъемной ей ватерлинии используется теорема Эйлера. Согласно этой теореме при бесконечно малом наклонении судна плоскости равнообъемных ватерлиний пересекаются по прямой, проходящей через их общий геометрический центр (центр тяжести), или ось бесконечно малого равнообъемного наклонения проходит через геометрический центр площади исходной ватерлинии.
Теорема Эйлера может быть применена и для конечных малых наклонений с той малой погрешностью, чем меньше угол наклонения.
Предполагается, что достаточная для практики точность обеспечивается при наклонениях Θ £ 10¸120 и Ψ £ 2¸30. В пределах этих углов и рассматривается начальная остойчивость судна.
Как известно из гл. 3, при плавании судна без крена и с дифферентом близким к нулю, ордината геометрического центра площади ватерлинии yf = 0, а абсциса xf ¹0. Потому в данном случае можно считать, что ось поперечного малого равнообъемного наклонения лежит в ДП, а ось продольного малого равнообъемного наклонения перпендикулярна ДП и смещена от пл. мидель – шпангоута на расстояние xf (рис.33).
Величина xf является функцией осадки судна d. Зависимость xf (d) представлена на кривых элементов теоретического чертежа.
При наклонении судна в произвольной плоскости ось равнообъемных наклонений также будет проходить через геометрический центр (центр тяжести) площади ватерлинии.
Метацентры и метацентрические радиусы
Предположим, что судно из исходного положения без крена и дифферента совершает поперечные или продольные равнообъемные наклонения. При этом плоскостью продольных наклонений будет вертикальная плоскость, которая совпадает с ДП, а плоскость поперечных наклонений – вертикальная плоскость, которая совпадает с плоскостью шпангоута, проходящего через ЦВ.
|
|
|
5.3.1. Поперечные наклонения. В прямом положении судна ЦВ находится в ДП (точка С) и линия действия силы плавучести γV также лежит в ДП (рис. 34). При поперечном наклонении судна на угол Θ изменяется форма погруженного объема, ЦВ перемещается в сторону наклонения из точки С в точку СΘ и линия действия силы плавучести будет наклонена к ДП под углом Θ.
Точка пересечения линий действия силы плавучести при бесконечно малом поперечном равнообъемном наклонении судна называется поперечным метацентром (точка m на рис.34). Радиус кривизны траектории ЦВ r (возвышение поперечного метацентра над ЦВ) называется поперечным метацентрическим радиусом.
В общем случае траектория ЦВ является сложной пространственной кривой и каждому углу наклонения соответствует свое положение метацентра (рис.35). Однако для малых равнообъемных наклонений с известным приближением можно принять, что траектория
ЦВ лежит в плоскости наклонения и является дугой окружности с центром в точке m. Таким образом, можно считать, что в процессе малого поперечного равнообъемного наклонения судна из прямого положения поперечный метацентр лежит в ДП и своего положения не меняет (r = const).
 |
 |
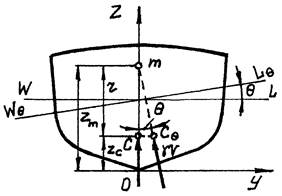Рис.34. Перемещение ЦВ при Рис.35. Перемещение ЦВ при
малых наклонениях больших наклонениях
 |
Выражение для поперечного метацентрического радиуса r получим из условия, что ось малого поперечного равнообъемного наклонения судна лежит в ДП и что при таком наклонении клиновидный объем v как бы переносится с борта, вышедшего из воды, на борт, вошедший в воду (рис.36).
Рис.36. К выводу выражения для поперечного метацентрического радиуса
Согласно известной теореме механики при перемещении тела, принадлежащей системе тел, центр тяжести всей системы перемешается в том же направлении параллельно перемещению тела, причем эти перемещения обратно пропорциональны силам тяжести тела и системы соответственно. Эту теорему можно распространить и на объемы однородных тел. Обозначим: С СΘ – перемещение ЦВ (геометрического центра объема V), b – перемещение геометрического центра клиновидного объема v. Тогда в соответствии с теоремой
|
|
|
= 
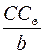, откуда: С СΘ = 
.
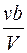Для элемента длины судна dx, полагая, что клиновидный объем имеет в плоскости шпангоута форму треугольника, получим:
dv 
dx 
y tgΘ y,
или при малом угле dv y2 Θ dx.
Если b 
y, тогда: dv b = 
y3 Θ dx.
Интегрируя, получим: v b = Θ 
y3 dx,
или: v b = ΘJx,
где Jx = 
y 
dx – момент инерции площади ватерлинии относительно продольной центральной оси.
Тогда выражение для перемещения ЦВ будет иметь вид:
С СΘ = 
Θ.
Как видно из рис. 36, при малом угле Θ
С СΘ r Θ.
Сопоставляя выражения, найдем, что поперечный метацентрический радиус:
r = .
Аппликата поперечного метацентра:
zm = zc + r = zc + .
5.3.2. Продольные наклонения (рис.37). По аналогии с поперечными наклонениями точка пересечения линий действия силы плавучести при бесконечно малом продольном равнообъемном наклонении судна называется продольным метацентром (точка М на рис.37). Возвышение продольного метацентра над ЦВ называется продольным метацентрическим радиусом. Величина продольного радиуса определяется выражением:
R = 
,
где Jyf – момент инерции площади ватерлинии относительно поперечной центральной оси.
Рис.37.К выводу выражения
для продольного
метацентрического радиуса
Аппликата продольного метацентра:
zм= zc + R = zc + .
Так как площадь ватерлинии вытянута в продольном направлении, то Jyf намного превышает Jx и соответственно R значительно больше r. Величина R составляет 1 
2 длины судна.
Метацентрические радиусы и аппликаты метацентров являются, как это будет ясно из последующего рассмотрения, важными характеристиками остойчивости судна. Значения их определяются при расчете элементов погруженного объема и для судна, плавающего без крена и дифферента, представляются кривыми Jx (d), Jyf (d), r(d), R(d) на чертеже кривых элементов теоретического чертежа (рис. 21).
|
|
|
