Остойчивость формы и остойчивость нагрузки

Рассмотрение этого вопроса позволяет установить природу остойчивости, выяснить физические причины возникновения восстанавливающего момента при наклонениях судна. В соответствии с метацентрическими формулами остойчивости (углы Θ и Ψ выражены в радианах):

m_Θ = γV h Θ = γV (r – α) Θ = γV r Θ – γV α Θ;

М_Ψ = γV Н Ψ = γV (R – α) Ψ = γV R Ψ – γV α Ψ.

Таким образом, восстанавливающие моменты m_Θ, М_Ψ и плечи статической остойчивости l_Θ, l _Ψ представляют собой алгебраическую сумму их составляющих:

m_Θ = m_ф + m_н; М_Ψ = М_ф + М_н;

l_Θ = l_фΘ + l_нΘ; l _Ψ = l _фΨ + l _нΨ,

где моменты

m_ф = γV r Θ;

М_ф= γV R Ψ,

принято называть моментами остойчивости формы, моменты

m_н = – γV α Θ;

М_н = – γV α Ψ,

моментами остойчивости нагрузки, а плечи

 

l_фΘ = m_ф / γV;

l_фΨ = М_ф / γV,

поперечными и продольными плечами остойчивости формы, плечи

l_нΘ = – m_н / γV;

l_нΨ = – М_н / γV,

поперечными и продольными плечами остойчивости нагрузки.

Так как: r = ; R = ; α = z_g – z_c,

где J_x и J_yf – момент инерции площади ватерлинии относительно поперечной и продольной центральной оси соответственно, то моменты формы и нагрузки можно представить в виде:

m_ф = γ J_x Θ, М_ф= γ J_yf Ψ;

m_н = – γV (z_g – z_c) Θ, М_н = – γV(z_g – z_c) Ψ.

По своей физической природе момент остойчивости формы всегда действует в сторону, противоположную наклонению судна, и, следовательно, всегда обеспечивает остойчивость. Он вычисляется через момент инерции площади ватерлинии относительно оси наклонения. Именно остойчивость формы предопределяет значительно большую продольную остойчивость по сравнению с поперечной т.к. J_yf» J_x.

Момент остойчивости нагрузки из-за положения ЦТ выше ЦВ α = (z_g – z_c) > 0, всегда уменьшает остойчивость судна и по существу она обеспечивается только остойчивостью формы.

Можно предположить, что в случае отсутствия ватерлинии, например, у подводной лодки в подводном положении, момент формы отсутствует (J_x = 0). В подводном положении подводная лодка за счет балластировки специальных цистерн, имеет положение ЦТ ниже ЦВ, в результате ее остойчивость обеспечивается остойчивостью нагрузки.

 

Определение мер начальной остойчивости

Судна

 

5.7.1. Посадка судна прямо и на ровный киль. В случаях, когда судно плавает с незначительными углами крена и дифферент, меры начальной остойчивости могут быть определены с помощью метацентрических диаграмм.

При заданной массе судна, определение мер начальной остойчивости сводится к определению аппликат метацентров (или метацентрических радиусов и аппликаты ЦВ) и аппликаты ЦТ.

 

Аппликата ЦВ z_c и метацентрические радиусы r, R являются характеристиками погруженного объема судна и зависят от осадки. Эти зависимости представлены на метацентрической диаграмме входящей в состав кривых элементов теоретического чертежа (рис.21). По метацентрической диаграмме (рис.42) можно не только определить z_c и r, но при известной аппликате ЦТ, найти поперечную метацентрическую высоту судна.

На рис.42 представлена последовательность расчета поперечной метацентрической высоты судна при приеме груза. Зная массу принятого груза m и аппликату его центра тяжести z, можно определить новую аппликату ЦТ судна z_g1 по формуле:

z_g1 = z_g + (z– z_g),

где z_g – аппликата ЦТ судна до приема груза.

5.7.2. Посадка судна с дифферентом. При плавании судна с дифферентом в воду входят более полные участки корпуса, что приводит к увеличению площади ватерлинии (остойчивости формы) и соответственно поперечной метацентрической высоты. У промысловых судов кормовые обводы полнее носовых, поэтому следует ожидать при дифференте на корму увеличение, а при дифференте на нос уменьшение поперечной остойчивости судна.

 

Рис.42. Метацентрическая Рис.43. Диаграмма Фирсова – Гундобина

диаграмма

 

Для вычисления поперечной метацентрической высоты судна с учетом дифферента используют диаграммы Фирсова – Гундобина, начальной остойчивости КТИРПиХ и интерполяционные кривые.

Диаграмма Фирсова – Гундобина (рис.43), отличается от диаграммы Фирсова тем, что содержит кривые z_m и z_c, значения которых определяются по известным осадкам судна носом и кормой.

Диаграмма начальной остойчивости КТИРПиХ (рис.44) позволяет определить аппликату метацентра судна z_m по известной массе Δ и абсциссе его центра тяжести x_g.

По диаграмме интерполяционных кривых (рис.45) можно при известных осадках судна носом и кормой найти поперечный метацентрический радиус r и аппликату центра величины судна z_c.

Диаграммы, показанные на рис. 43 – 45, позволяют найти z_m при любой посадке судна, в том числе и на ровный киль. Следовательно, они дают возможность проанализировать влияние дифферента на начальную поперечную остойчивость судна.

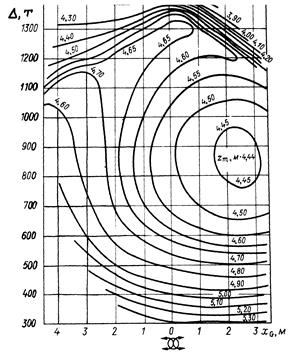
Рис.44. Диаграмма начальной Рис.45.Диаграмма для определения z_c и r

остойчивости траулера типа “Карелия“

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: