 |
Понятие степени с рациональным показателем
|
|
|
|
Тематические обзоры по курсу элементарной математики
Составитель В.Г.Ермаков
Тема 3. Степень числа с рациональными показателями [1]
3.1. Корень 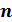 -ой степени
-ой степени
Определение. Пусть  есть натуральное число и
есть натуральное число и  . Корнем степени
. Корнем степени  из числа
из числа  называют такое число (если оно существует),
называют такое число (если оно существует),  -я степень которого равна
-я степень которого равна  .
.
Корень степени 2 называют также квадратным корнем. Корень степени 3 называют ещё кубическим корнем.
Пример 1. Равенства  показывают, что числа
показывают, что числа  есть кубические корни соответственно из чисел
есть кубические корни соответственно из чисел 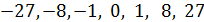 .
.
Пример 2. Равенства  показывают, что числа
показывают, что числа  есть корни степени 5 соответственно из чисел
есть корни степени 5 соответственно из чисел 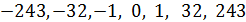 .
.
Эти примеры указывают на то, что корни 3-й и 5-й степеней из действительных чисел существуют.
Пример 3. Равенства  показывают, что есть два числа
показывают, что есть два числа  и
и  , которые являются корнями четвертой степени из
, которые являются корнями четвертой степени из  ; есть два числа
; есть два числа  и
и  , являющиеся корнями четвертой степени из 16; есть также два числа
, являющиеся корнями четвертой степени из 16; есть также два числа 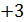 и
и  , являющиеся корнями четвертой степени из 81. Далее, 0 есть корень четвертой степени из 0.
, являющиеся корнями четвертой степени из 81. Далее, 0 есть корень четвертой степени из 0.
Этот пример указывает на то, что корень 4-й степени из неотрицательных чисел существует. Не существует корня четвертой степени из отрицательного числа, потому что четвертая степень любого действительного числа есть число неотрицательное.
Справедливы следующие теоремы.
Теорема 1. Существует, и притом, единственный, корень нечетной степени из любого действительного числа  , при этом корень нечетной степени: а) из положительного числа есть число положительное; б) из отрицательного числа есть число отрицательное; в) из нуля есть нуль.
, при этом корень нечетной степени: а) из положительного числа есть число положительное; б) из отрицательного числа есть число отрицательное; в) из нуля есть нуль.
Теорема 2. Существуют два и только два корня четной степени из любого положительного числа, которые отличаются только знаками. Корень четной степени из 0 единственный, равный нулю. Корня четной степени из отрицательного числа не существует.
|
|
|
В школьном курсе математики эти теоремы доказывают при помощи графического метода, то есть путём анализа графика функции  соответственно при нечётных и чётных значениях показателя
соответственно при нечётных и чётных значениях показателя  . Строгое доказательство этих теорем опирается на теорию непрерывных функций, составляющую часть курса высшей математики, изучаемого в высших учебных заведениях.
. Строгое доказательство этих теорем опирается на теорию непрерывных функций, составляющую часть курса высшей математики, изучаемого в высших учебных заведениях.
Арифметический корень
Определение. Пусть  есть натуральное число и
есть натуральное число и  . Неотрицательный корень степени
. Неотрицательный корень степени  из неотрицательного числа
из неотрицательного числа  называют арифметическим корнем степени
называют арифметическим корнем степени  из числа
из числа  .
.
Как уже было отмечено в предыдущем пункте, для нечетного  существует только один корень из любого числа
существует только один корень из любого числа  . При этом он неотрицательный, если
. При этом он неотрицательный, если  неотрицательно. Поэтому понятие корня нечетной степени из неотрицательного числа
неотрицательно. Поэтому понятие корня нечетной степени из неотрицательного числа  и понятие арифметического корня той же степени из того же самого числа
и понятие арифметического корня той же степени из того же самого числа  совпадают. В случае же четного
совпадают. В случае же четного  существуют два корня степени
существуют два корня степени  из положительного числа. Один из них является положительным, то есть является арифметическим корнем степени
из положительного числа. Один из них является положительным, то есть является арифметическим корнем степени  из числа
из числа  (его обозначают
(его обозначают  ), а другой равен ему по абсолютной величине, но противоположен по знаку (он равен
), а другой равен ему по абсолютной величине, но противоположен по знаку (он равен  ). Корень степени
). Корень степени  из нуля по определению есть арифметический корень степени
из нуля по определению есть арифметический корень степени  из нуля:
из нуля:  .
.
Следует подчеркнуть, что:
1) если  – неотрицательное число, а
– неотрицательное число, а  – любое натуральное число
– любое натуральное число  , то запись
, то запись  означает арифметический корень степени
означает арифметический корень степени  из числа
из числа  .
.
2) если  – отрицательное число и
– отрицательное число и  – нечётное число, то запись
– нечётное число, то запись  означает корень степени
означает корень степени  из числа
из числа  , но этот корень не является арифметическим корнем;
, но этот корень не является арифметическим корнем;
3) если  – отрицательное число и
– отрицательное число и  – чётное число, то запись
– чётное число, то запись  не имеет смысла.
не имеет смысла.
Теорема 3. Для натурального числа  и неотрицательного числа
и неотрицательного числа  справедливы равенства:
справедливы равенства:
 , ,
| (1) |

| (2) |
Доказательство. Так как  – неотрицательное число, то
– неотрицательное число, то  по определению есть неотрицательное число,
по определению есть неотрицательное число,  -я степень которого равна
-я степень которого равна  . Равенство (1) это и выражает.
. Равенство (1) это и выражает.
|
|
|
Так как  – неотрицательное число, то, как следует из теорем 2д и 3д Дополнения 1,
– неотрицательное число, то, как следует из теорем 2д и 3д Дополнения 1,  . При этом
. При этом  по определению есть неотрицательное число, n -я степень которого есть
по определению есть неотрицательное число, n -я степень которого есть 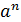 . Таким числом, очевидно, является число
. Таким числом, очевидно, является число  , что и выражает равенство (2). Заметим, что другого неотрицательного числа, n -я степень которого равняется
, что и выражает равенство (2). Заметим, что другого неотрицательного числа, n -я степень которого равняется 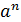 , нет.
, нет.
Последнее утверждение докажем методом от противного. В самом деле, допустим, что существует положительное число  , такое, что
, такое, что 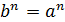 , но при этом
, но при этом  . Тогда возможны 2 случая: либо
. Тогда возможны 2 случая: либо  , либо
, либо  . В силу теоремы 3д Дополнения 1 в первом случае
. В силу теоремы 3д Дополнения 1 в первом случае  , а во втором случае
, а во втором случае  , что противоречит равенству
, что противоречит равенству 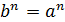 . Из полученного противоречия вытекает, что указанное число
. Из полученного противоречия вытекает, что указанное число  является единственным.
является единственным.
Теорема 3 доказана.
Соображения, использованные при доказательстве теоремы 3, позволяют сформулировать и доказать ещё одну важную вспомогательную теорему.
Теорема 4. Для любого натурального числа  и любых неотрицательных действительных чисел
и любых неотрицательных действительных чисел  и
и  из равенства
из равенства  следует
следует 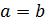 .
.
Доказательство. Применим метод доказательства от противного. Предположим, что числа  и
и  неотрицательны,
неотрицательны,  , но
, но  . Тогда возможны 2 случая: либо
. Тогда возможны 2 случая: либо  , либо
, либо  . В силу теоремы 3д Дополнения 1 и замечания к этой теореме в первом случае
. В силу теоремы 3д Дополнения 1 и замечания к этой теореме в первом случае  , а во втором случае
, а во втором случае  , что противоречит равенству
, что противоречит равенству  . Из полученного противоречия вытекает, что допущение о том, что
. Из полученного противоречия вытекает, что допущение о том, что  , является ошибочным. Но тогда
, является ошибочным. Но тогда 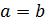 . Теорема 4 доказана.
. Теорема 4 доказана.
Теорема 4'. Для любого нечётного натурального числа 
 и любых действительных чисел
и любых действительных чисел  и
и  из равенства
из равенства  следует
следует 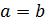 .
.
Доказательство. В случае, когда оба числа  и
и  неотрицательны, данное утверждение является частью теоремы 4. Для случая, когда оба эти числа отрицательны, доказательство теоремы 4 можно повторить почти дословно, но опорной теоремой должна послужить не теорема 3д из Дополнения 1, а близкая к ней теорема 5д. Наконец, в случае, когда числа
неотрицательны, данное утверждение является частью теоремы 4. Для случая, когда оба эти числа отрицательны, доказательство теоремы 4 можно повторить почти дословно, но опорной теоремой должна послужить не теорема 3д из Дополнения 1, а близкая к ней теорема 5д. Наконец, в случае, когда числа  и
и  имеют разные знаки, легко заметить, что их n -е степени
имеют разные знаки, легко заметить, что их n -е степени 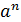 и
и  тоже имеют разные знаки, следовательно, и в этом случае доказательство можно провести методом от противного.
тоже имеют разные знаки, следовательно, и в этом случае доказательство можно провести методом от противного.
Замечание. При доказательстве следующих теорем будут использованы свойства степени числа с целыми показателями, доказанные ранее.
Теорема (напоминание). Пусть  и
и  – произвольные действительные числа, отличные от нуля, а
– произвольные действительные числа, отличные от нуля, а  и
и  – произвольные целые числа. Тогда
– произвольные целые числа. Тогда
|
|
|
 ; ;
| (1н) |
 ; ;
| (2н) |
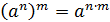 ; ;
| (3н) |
 ; ;
| (4н) |

| (5н) |
Теорема 5. Для любого натурального числа  и любых неотрицательных действительных чисел
и любых неотрицательных действительных чисел  ,
,  и
и  справедливы равенства
справедливы равенства
 ; ;
| (3) |

| (4) |
Доказательство. Возведём левую часть доказываемого равенства (3) в степень  . По свойству (1), которое является прямым следствием определения корня -ой степени из неотрицательного действительного числа, имеем
. По свойству (1), которое является прямым следствием определения корня -ой степени из неотрицательного действительного числа, имеем

Далее, возведём в степень  правую часть доказываемого равенства (3). В силу свойств (1н) и (1) имеем
правую часть доказываемого равенства (3). В силу свойств (1н) и (1) имеем

Правые части двух последних равенств равны, следовательно, равны и их левые части, то есть

Так как числа  и
и  неотрицательны, то, применяя теорему 4, получаем, что равенство (3) справедливо.
неотрицательны, то, применяя теорему 4, получаем, что равенство (3) справедливо.
Аналогично доказывается и равенство (4). Теорема 5 доказана.
Теорема 6. Для любых натуральных чисел  и
и 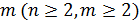 и любого неотрицательного действительного числа
и любого неотрицательного действительного числа  справедливы равенства
справедливы равенства
 ; ;
| (5) |
 ; ;
| (6) |
 . .
| (7) |
Доказательство. По условию теоремы 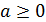 , поэтому числа, стоящие в левых и правых частях доказываемых равенств (5) – (7), определены и неотрицательны. Данное обстоятельство позволяет доказывать эти равенства с опорой на теорему 4.
, поэтому числа, стоящие в левых и правых частях доказываемых равенств (5) – (7), определены и неотрицательны. Данное обстоятельство позволяет доказывать эти равенства с опорой на теорему 4.
Для доказательства равенства (5) возведём его левую и правую части в степень  :
:


Из доказанного равенства 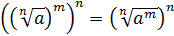 в силу теоремы 4 вытекает справедливость равенства (5).
в силу теоремы 4 вытекает справедливость равенства (5).
Для доказательства равенства (6) возведём его левую и правую части в степень  :
:
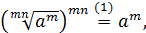
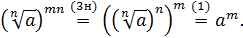
Из доказанного равенства  в силу теоремы 4 вытекает справедливость равенства (6).
в силу теоремы 4 вытекает справедливость равенства (6).
Для доказательства равенства (7) возведём его левую и правую части в степень  :
:


Из доказанного равенства  в силу теоремы 4 вытекает справедливость равенства (7).
в силу теоремы 4 вытекает справедливость равенства (7).
Теорема 6 доказана.
Замечание. Если  и
и  – нечётные числа, то равенства (5) – (7) справедливы для любых действительных чисел
– нечётные числа, то равенства (5) – (7) справедливы для любых действительных чисел  , необязательно неотрицательных. Доказательство этого утверждения можно получить дословным повторением доказательства теоремы 6, но главной опорой при этом должна быть не теорема 4, а теорема 4'.
, необязательно неотрицательных. Доказательство этого утверждения можно получить дословным повторением доказательства теоремы 6, но главной опорой при этом должна быть не теорема 4, а теорема 4'.
Теорема 7. Для любого натурального числа  и любого действительного числа
и любого действительного числа  справедливо равенство
справедливо равенство
|
|
|

| (8) |
Доказательство. Пусть  есть произвольное действительное число. Тогда
есть произвольное действительное число. Тогда

Поэтому в силу равенства (2)

что и требовалось доказать.
Теорема 7 доказана.
Теорема 8. Пусть  – положительное число,
– положительное число,  – целое число и
– целое число и  – натуральное число,
– натуральное число,  . Тогда справедливо равенство
. Тогда справедливо равенство
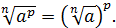
| (9) |
Доказательство. Если  – натуральное число, то в этом случае равенство (9) совпадает со свойством (5) и потому уже доказано.
– натуральное число, то в этом случае равенство (9) совпадает со свойством (5) и потому уже доказано.
Если  , то
, то

Следовательно,  .
.
Если  , то
, то  , где
, где  – натуральное число. Тогда, используя определение степени с отрицательным целым показателем и свойства арифметических корней степени
– натуральное число. Тогда, используя определение степени с отрицательным целым показателем и свойства арифметических корней степени  , получаем:
, получаем:

Теорема 8 доказана.
Понятие степени с рациональным показателем
Ранее уже было введено и исследовано понятие степени с натуральным показателем, а затем и с целым показателем. Теперь определим степень с рациональным показателем, т. е. с показателем  , где
, где  – целое число, а
– целое число, а  – натуральное число,
– натуральное число,  .
.
Определение. Пусть 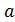 – произвольное положительное действительное число, а
– произвольное положительное действительное число, а  – рациональное число,
– рациональное число,  . По определению
. По определению  в степени
в степени  равно арифметическому корню степени
равно арифметическому корню степени  из
из  в степени
в степени  , то есть по определению
, то есть по определению
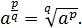
Например:  ,
, 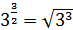 ,
, 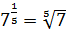 ,
,  .
.
Теорема 9. Пусть  – произвольное положительное действительное число,
– произвольное положительное действительное число,  – целое число,
– целое число,  и
и  – натуральные числа,
– натуральные числа,  ;
;  . Тогда справедливы
. Тогда справедливы
равенства

| (11) |

| (12) |

| (13) |
Доказательство. Используя определение степени с рациональным показателем, доказанные ранее свойства степени с целым показателем и свойства арифметического корня, получаем:

Здесь def – сокращение от definition (определение, дефиниция).
Равенство (11) доказано.
Докажем теперь равенство (12).

Равенство (12) доказано.
Докажем равенство (13).

Равенство (13) и теорема 9 доказаны.
Замечание 1. Если  и
и  – натуральные числа, а
– натуральные числа, а  – целое число, то справедливо равенство
– целое число, то справедливо равенство  . Поэтому если
. Поэтому если  , то для любого натурального числа
, то для любого натурального числа  имеем также
имеем также  .
.
Равенство (12) показывает, что определение степени  с рациональным показателем
с рациональным показателем  не зависит от формы записи числа
не зависит от формы записи числа  , а зависит лишь от самого числа
, а зависит лишь от самого числа  . При любой форме записи данного рационального числа определение
. При любой форме записи данного рационального числа определение  приводит к одному и тому же числу. Если бы это было не так, то определение степени с рациональным показателем было бы противоречивым.
приводит к одному и тому же числу. Если бы это было не так, то определение степени с рациональным показателем было бы противоречивым.
Замечание 2. Равенство (13) показывает, что определение степени с рациональным показателем содержит в себе определение степени с целым показателем.
|
|
|


