 |
Свойства степени с рациональным показателем
|
|
|
|
Теорема 10. Пусть 
и 
– произвольные положительные действительные числа,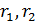 
и 
– произвольные рациональные числа. Тогда справедливы свойства:
 ;
| (14) |
 ;
| (15) |
 ;
| (16) |
 ;
| (17) |
 ;
| (18) |
 ;
| (19) |
| (20) |
Доказательство. Для доказательства свойства (14) запишем число в виде 
, где 
– натуральное число, 
, а а 
– целое число (положительное, отрицательное или нуль). Так как – положительное число, то, используя определение степени с рациональным показателем и свойства корня степени 
, получим, что
т. е. при 
неравенство (14) верно.
Используя свойства степени положительного числа с целым показателем, получаем, что при любом целом числе 
Неравенство (14) доказано в общем случае.
Для доказательства равенства (15) представим числа 
и 
в виде 
и 
, где 
и 
– целые числа, а 
и 
– натуральные числа, 
; 
. Используя определение степени с рациональным показателем, свойства арифметических корней и свойства степеней с целым показателем, получим:
Свойство (15) доказано.
Теперь на основании свойства (15) имеем
откуда и следует равенство (16).
Далее, в силу свойств (15) и (16)
и тем самым свойство (17) доказано.
Теперь докажем свойство (18). Пусть и – произвольные рациональные числа. Представим их в виде и , где и – целые числа, а и – натуральные числа, ; . Тогда, вновь используя определение степени с рациональным показателем, свойства арифметических корней и свойства степеней с целым показателем, получим:
Свойство (18) доказано.
Для доказательства свойства (19) представим рациональное число в виде , где – целое число, а – натуральное число, . Тогда, используя определение степени с рациональным показателем, свойства арифметических корней и свойства степеней с целым показателем, получим:
|
|
|
и равенство (19) доказано.
Аналогично этому свойству доказывается и свойство (20).
Теорема 10 доказана.
Теорема 11. Пусть число 
, а – рациональное число. Тогда
Доказательство. Представим рациональное число в виде , где – целое число, а – натуральное число, .
Так как , то верно равенство
В случае, когда 
, имеем 
и
а в случае, когда 
, имеем 
, 
и
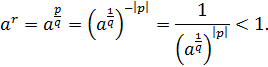
Теорема 11 доказана.
Теорема 12. Пусть , а рациональные числа и удовлетворяют неравенству
|
Тогда
| (21) |
Доказательство. Используя свойства степени с рациональным показателем, представим разность 
следующим образом:
Согласно свойству (14) (теорема 10) 
для любого рационального числа . Далее, так как 
, то по теореме 11 
, поэтому 
. Следовательно, 
и 
.
Теорема 12 доказана.
Теорема 13. Если число находится в интервале 
, а рациональные числа и удовлетворяют неравенству
|
то
| (22) |
Доказательство. Поскольку , то 
. Применяя к числу 
теорему 12, получаем:
|
откуда
| (23) |
Так как и 
, то, умножая обе части неравенства (23) на 
приходим к искомому неравенству (22).
Теорема 13 доказана.
Исторические сведения
Как известно, греки знали квадратные корни задолго до новой эры. Способы извлечения корня степени также известны давно. Например, хорезмский математик Бируни (972 – 1048) в своей книге «Ключи к арифметике» описывает способ извлечения корня с любым натуральным показателем. Впрочем, способ этот громоздкий и неудобный. Начиная с XIII в. итальянские и другие европейские математики обозначали корень латинским словом Radix (корень) или сокращенно R. Так, Н. Шюке в XV в. писал 
вместо принятого теперь 
.
Немецкие математики в рукописи 1480 г., написанной, как это было тогда принято, на латинском языке, обозначали корень квадратный знаком (
), корень четвертой степени знаком ( ), корень кубический знаком ( ).
В 1626 г. нидерландский математик А. Жирар ввел близкое к современному обозначение для квадратных, кубических и т. д. корней: 
….
|
|
|
Выдающемуся итальянскому математику Д. Кардано (1501 – 1576) принадлежат формулы решения кубических уравнений, в которых используются кубические корни.
Равенство 
(для 
) применял в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель ввел и Н. Шюке.
В XVI в. фламандский ученый С. Стевин (1548 – 1620) предложил понимать 
как степень числа с дробным показателем 
, т. е. 
. Систематически нулевые, отрицательные и дробные показатели стал применять И. Ньютон (1643 – 1727).
Рациональная степень числа позволила определить показательную функцию 
, существенный вклад в изучение которой внес Л. Эйлер (1707 – 1783).
|
|
|
