 |
Дополнение 1. Метод математической индукции
|
|
|
|
Сформулируем принцип полной индукции.
Если свойство, зависящее от натурального 
, во-первых, верно при 
и, во-вторых, из предположения, что оно верно при 
, следует, что оно верно при 
, то считают, что это свойство верно для любого натурального 
. Продемонстрируем возможности применения метода математической индукции в процессе доказательства несколько теорем.
Теорема 1д. Если 
, то для любого натурального
 .
| (1д) |
Доказательство. Согласно принципу полной индукции, для того чтобы неравенство (1д) можно было считать верным для всех натуральных , достаточно проверить, что выполняются следующие два утверждения:
1) неравенство (1д) справедливо для ;
2) если допустить, что для некоторого неравенство (1д) справедливо, то есть имеет место неравенство 
, то оно справедливо и для , то есть имеет место неравенство 
.
Утверждение 1 действительно выполняется, потому что, положив в неравенстве (1д) , получим неравенство , верное по условию. Утверждение 2 тоже выполняется, ведь если предположить верным неравенство , то после умножения его на положительное
число 
получим верное неравенство .
Таким образом, утверждения 1 и 2 выполняются. Но тогда согласно принципу полной индукции неравенство (1д) верно для любого натурального . Теорема 1д доказана.
Замечание. Доказательство, основанное на принципе индукции, называют доказательством по индукции или доказательством методом математической индукции.
Теорема 2д. Для любого натурального
 .
| (2д) |
Доказательство. При равенство (2д) очевидно. Если допустить, что равенство 
доказано, то отсюда будет следовать, что 
.
Тогда согласно принципу полной индукции равенство (2д) надо считать верным для любого натурального . Теорема 2д доказана.
|
|
|
Теорема 3д. Если 
, то для любого натурального
 .
| (3д) |
Доказательство. Это утверждение доказывают по индукции следующим образом. При неравенство (3д) верно, так как по условию 
.
Пусть при равенство (3д) верно, т. е.
 .
| (4д) |
Так как по условию – положительное число, то и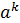 
– положительное число, что было доказано выше. Умножив неравенство на 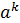и неравенство (4д) на 
, получим 
и 
, откуда следует, что 
. Тогда согласно принципу полной индукции неравенство (3д) надо считать верным для любого натурального . Теорема 3д доказана.
Замечание. Теорема 3д остаётся верной и в случае, если 
, так как в силу теорем 1д и 2д при 
имеем: 
, а 
, то есть и в этом случае .
Теорема 4д. Для любых действительных чисел и и для любого натурального числа 
справедливо равенство
 .
| (5д) |
Доказательство. Это утверждение докажем по индукции.
При 
равенство (5д) верно, поскольку представляет собой известную формулу сокращенного умножения: 
.
Пусть при равенство (5д) верно, то есть
 .
| (6д) |
Умножая левую и правую часть равенства (6д) на , получаем:
 .
| (7д) |
К левой части равенства (7д) прибавим 
, а к правой части прибавим такое же слагаемое, представив его в виде 
. В результате простых преобразований окончательно получаем:
 .
| (8д) |
Итак, доказаны 2 утверждения: 1) равенство (5д) справедливо при ,
2) из справедливости равенства (5д) при следует, что оно верно и при . В силу принципа математической индукции отсюда следует, что равенство (5д) верно для любого натурального числа .
Теорема 4д доказана.
Теорема 5д. Если 
, то для любого нечётного натурального 
| ,
| (9д) |
а для любого чётного натурального 
 .
| (10д) |
Это утверждение докажем отталкиваясь от равенства (5д). Во-первых, отметим, что по условию , поэтому 
, так что первый множитель в правой части равенства (5д) является отрицательным. Во-вторых, так как 
, то 
. Поэтому
Отсюда следует, что
|
|
|
и значит, второй множитель в правой части равенства (5д) имеет тот же знак, что и 
, то есть он положителен при нечётном и отрицателен при чётном . Окончательно из равенства (5д) с учетом неравенства получаем, что при нечётном 
и потому , а при чётном 
и, следовательно, .
Теорема 5д доказана.
[1] Здесь использованы материалы из учебника: Алгебра, 9 / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2001. – 255 с.
|
|
|
