Показатели изменения уровней ряда динамики: абсолютные и относительные, базисные, цепные. Абсолютные приросты

Задачи, возникающие при изучении динамических рядов:

1) характеристика интенсивности отдельных изменений в уровнях рода от периода к периоду или от даты к дате;

2) определение средних показателей временного ряда за тот или иной период;

3) выявление основных закономерностей динамики исследуемого явления на отдельных этапах и в целом за рассматриваемый период;

4) выявление факторов, обусловливающих изменение изучаемого объекта во времени;

5) прогноз развития явления на будущее.

Эти задачи решаются с помощью показателей изменения уровней ряда динамики.

Способы сопоставления уровней ряда:

1) каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, где базисный уровень - начальный уровень дина­мического ряда или уровень, с которого начинается какой-то новый этап развития - это сравнение с постоянной базой. Полученные при этом показатели называются базисными;

2) каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим - это сравнение с переменной базой. Полученные при этом показатели называются цепными.

Показатели динамики с постоянной базой (базисные показатели) - это показатели окончательного результата всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до назначенного (/-того) периода.

Показатели динамики с переменной базой (цепные показатели) - это показатели интенсивности изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.

Абсолютный прирост ( _i) – это разность между двумя уровнями динамического ряда, которая пока­зывает, насколько данный уровень ряда превышает уровень, принятый за базу сравнения.

Формула расчета абсолютного прироста:

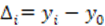
где _i - абсолютный прирост;

y_i - уровень сравниваемого периода;

y₀ - уровень базисного периода.

Формула расчета абсолютного прироста при сравнении с переменной базой:

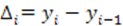
где 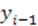- уровень предшествующего периода.

Если уровень уменьшился по сравнению с базисным, то <0. В этом случае абсолютный прирост характеризует абсолютное уменьшение (сокращение) уровня.

Абсолютная скорость роста (снижения) уровня - абсолютный прирост за единицу времени с переменной базой.

Абсолютное ускорение - разность между абсолютным приростом за данный период и абсолютным приростом за предыдущий период одинаковой дли­тельности:

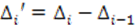
Абсолютное ускорение может быть:

1) положительное число;

2) отрицательное число.

Абсолютное ускорение показывает, насколько увеличилась (уменьшилась) скорость изменения показателя. Показатель ускорения применяется для цепных абсолютных приростов. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда.

Абсолютные приросты для любых рядов динамики являются интервальными показателями, т. е. характеризуют тот или иной промежуток (интервал) времени

 

2. Понятие абсолютной и относительной величины. Проценты. Расчет темпов роста и темпов прироста при цепном способе вычисления Практический пример.

 

3. Понятие закона распределения случайной величины. Ряд распределения. Практический пример.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.

Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать.

Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.

Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х₁, х₂,..., х_n с соответствующими им вероятностями р₁, р₂,..., р_n:

хi	x1	x2	...	xn
pi	p1	p2		pn

Примерами дискретной случайной величины являются: число бракованных изделий в случайно отобранной партии из n -изделий; число солнечных дней в году; число учеников, опрошенных на уроке в школе.

Примерами непрерывной случайной величины служат: время безаварийной работы станка; расход горючего на единицу расстояния; количество осадков, выпавших за сутки

 

 

4. Числовые характеристики случайных величин. Написать и пояснить формулы математического ожидания, дисперсии и среднеквадратического отклонения. Практический пример.

Математическим ожиданием (средним значением) случайной величины X, заданной на дискретном вероятностном пространстве, называется число m = M[X] = ∑x_ip_i, если ряд сходится абсолютно.

Назначение сервиса. С помощью сервиса в онлайн режиме вычисляются математическое ожидание, дисперсия и среднеквадратическое отклонение. Кроме этого строится график функции распределения F(X).

Начало формы

Конец формы

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: