 |
Воспользовавшись разложением функции f(x) в ряд Фурье в указанном интервале, найти сумму данного числового ряда.
|
|
|
|
| 1. | 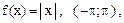
| 
|
| 2. | 
| 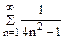
|
| 3. | 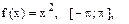
| 
|
| 4. | 
| 
|
| 5. | 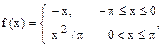
| 
|
| 6. | 
| 
|
| 7. | 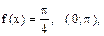
| 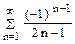
|
| 8. | 
| 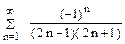
|
| 9. | 
| 
|
| 10 | 
| 
|
| 11. | 
| 
|
| 12. | 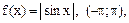
| 
|
| 13. | 
| 
|
| 14. | 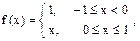
| 
|
| 15. | 
| 
|
| 16. | 
| 
|
| 17. | 
| 
|
| 18. | 
| 
|
| 19. | 
| 
|
| 20. | 
| 
|
| 21. | 
| 
|
| 22. | 
| 
|
| 23. | 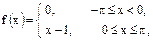
| 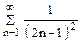
|
| 24. | 
| 
|
| 25. | 
| 
|
| 26. | 
| 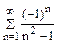
|
| 27. | 
| 
|
| 28. | 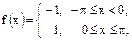
| 
|
| 29. | 
| 
|
| 30. | 
| 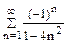
|
Контрольная работа № 7.
"Теория вероятностей"
Задание 7.1.
1. Каждая из двух команд по 5 спортсменов проводит жеребьевку для присвоения номеров. Два брата входят в состав разных команд. Найти вероятность того, что братья получат: а) номер 4; б) одинаковый номер.
2. Прибор содержит два одинаковых независимо функционирующих блока с вероятностями безотказной работы 0,8. Найти вероятность того, что безотказно будет работать: а) только один блок; б) хотя бы один блок.
3. База отправила товар в два магазина. Вероятность своевременной доставки в каждый из них равна 0,8. Найти вероятность того, что своевременно получит товар: а) только один магазин; б) хотя бы один магазин.
4. Рейсовый катер может опоздать вследствие двух независимых причин: плохой погоды и неисправности оборудования. Вероятность плохой погоды равна 0,3, вероятность неисправности 0,4. Найти вероятность того, что катер опоздает: а) только по причине плохой погоды; б) по любым причинам.
5. Условия дуэли предусматривают по 2 выстрела каждого из дуэлянтов по очереди до первого попадания. Вероятности их попадания при одном выстреле равны 0,2 и 0,3 соответственно. Найти вероятность того, что первый дуэлянт: а) поразит соперника вторым выстрелом; б) поразит соперника.
6. Вероятность забить гол нападающим при одном ударе по воротам равна 0,3. Найти вероятность того, что после двух ударов будет забит: а) только один гол; б) хотя бы один гол.
|
|
|
7. Вероятность своевременного обнаружения крылатой ракеты радиолокационной станцией (РЛС) равна 0,8. На дежурстве находятся две РЛС. Найти вероятность того, что ракета будет обнаружена: а) только одной РЛС; б) хотя бы одной РЛС.
8. Автомобильный номер содержит четыре цифры. Найти вероятность того, что у встречного автомобиля сумма цифр номера: а) равна двум; б) не более двух.
9. Найти вероятность того, что наугад названное двузначное число: а) делится на 3; б) имеет сумму цифр, равную 1.
10. В ящике пять белых и два красных шара. Найти вероятность того, что наугад извлеченные два шара будут: а) одного цвета; б) белые.
11. Двое независимо друг от друга садятся в электропоезд из восьми вагонов. Найти вероятность их встречи.
12. Ракета несет две разделяющиеся боеголовки, поражающие цель независимо друг от друга с вероятностями 0,8 и 0,7. Найти вероятность того, что цель будет поражена: а) только одной боеголовкой; б) хотя бы одной боеголовкой.
13. В ящике пять белых и три черных шара. Найти вероятность того, что наугад извлеченные два шара будут: а) разных цветов; б) черные.
14. Найти вероятность того, что двое встречных прохожих родились: а) в один месяц; б) летом.
15. Найти вероятность того, что сумма цифр наугад выбранного двузначного числа: а) равна пяти; б) меньше пяти.
16. Найти вероятность того, что произведение цифр наугад выбранного двузначного числа: а) равно трем; б) меньше трех.
17. Вероятности поймать рыбу при поклевке у рыболовов равны 0,2 и 0,3 соответственно. У каждого произошла одна поклевка. Найти вероятность того, что их общий улов составит: а) одну рыбу; б) не менее одной рыбы.
18. Телефонный номер содержит 6 цифр. Найти вероятность того, что сумма цифр наугад выбранного номера: а) равна 2; б) меньше 2.
19. Найти вероятность того, что при восьми случайных нажатиях на клавиши пишущей машинки будет напечатано слово "отлично". Клавиатура содержит 40 клавишей.
|
|
|
20. Два шахматиста играют между собой матч из двух партий. Вероятность выигрыша в каждой партии первым из них равна 0,6. Какова вероятность, что он выигрывает: а) только одну партию; 2) хотя бы одну партию.
21. Два стрелка произвели по одному выстрелу по мишени с вероятностью p1 = 0,6, p2 = 0,7. Найти вероятность: а) только одного попадания; б) хотя бы одного попадания.
22. Вероятности преодолеть планку для двух прыгунов равны p1 = 0,8, p2 = 0,7 соответственно. Найти вероятность того, что: а) только один из них возьмет высоту; б) хотя бы один из них возьмет высоту.
23. Автомобильный номер состоит из четырех цифр. Найти вероятность того, что номер встречного автомобиля содержит: а) три пятёрки подряд; б) три пятёрки.
24. К месту пожара направлены две команды, которые могут успеть к тушению своевременно с вероятностями p1 = 0,9, p2 = 0,8. Какова вероятность потушить пожар, если для этого: а) достаточно одной команды; б) необходимы обе команды.
25. Два самолета выпускают в цель по одной ракете с вероятностями попадания p1=0,8, p2=0,9. Найти вероятность поражения цели: а) двумя ракетами; б) только одной ракетой.
26. Прибор состоит из трех независимо друг от друга функционирующих блоков А, В, С с вероятностями безотказной работы Р(А)=0,9, Р(В)=0,8, Р(С)=0,7. Найти вероятность безотказной работы прибора, если для этого необходимо функционирование блока А и хотя бы одного из блоков В, С.
27. Вероятности выполнения месячного плана двумя цехами предприятия равны p1=0,9, p2=0,7. Полагая, что цеха работают независимо друг от друга, найти вероятности того, что: а) только один цех выполнит план; б) хотя бы один цех выполнит план.
28. Участок электрической цепи состоит из последовательно соединенных элементов А, В с вероятностями выхода из строя р1= 0,1, р2= 0,2. Элемент В дублируется с помощью параллельно включенного ему элемента С (р3 = 0,2). Найти вероятность безотказной работы участка: а) при отсутствии элемента С; б) при его наличии.
29. Два орудия выпускают в цель по одному снаряду с вероятностями попадания p1 = 0,6, p2 = 0,7. Найти вероятность того, что в цель попадет: а) только один снаряд; б) хотя бы один снаряд.
30. Болезни А, В имеют одинаковые симптомы, обнаруженные у больного. Вероятности заболеваний равны Р(А) = 0,3, Р(В) = 0,5. Считая, что человек может приобрести болезни независимо одну от другой найти вероятность того, что больной болен: а) только одной из болезней; б) хотя бы одной болезнью.
|
|
|
Задание 7.2.
1. 70% однотипных утюгов, поступающих в продажу изготовлено на предприятии А, 30% - на предприятии В. Доля брака на предприятии А - 5%, на предприятии В - 2%. а) Найти вероятность покупки бракованного утюга; б) купленный утюг оказался бракованным. Какова вероятность того, что он изготовлен на предприятии А?
2. В урне 2 белых и 3 черных шара. Наугад извлекается один из них и откладывается в сторону. Затем извлекается второй шар. а) Найти вероятность того, что он белый; б) извлеченный второй шар - белый. Какова вероятность, что первый шар был черным?
3. Прибор комплектуется узлом, изготавливаемым заводами 1 (поставляет 60% узлов), 2 (поставляет 40% узлов). Доля брака на заводе 1 - 0,05, на заводе 2 - 0,07. а) Найти вероятность того, что прибор - бракованный; б) прибор оказался бракованным. Найти вероятность, что виновник - завод 1.
4. При сборке подшипников используются шарики, 30% которых поставляет цех 1 и 70% - цех 2. Доли брака в цехах составляют 0,1 и 0,05 соответственно. а) Найти вероятность брака подшипника; б) подшипник оказался бракованным. Найти вероятность того, что виновником является цех 1.
5. В двух урнах лежат по 2 белых и 3 черных шара. Из первой во вторую наугад перекладывается шар, затем из второй извлекается шар. а) Найти вероятность того, что он - белый; б) извлеченный шар - белый. Какова вероятность, что перекладывался черный шар?
6. Два цеха выпускают по 50% однотипных телевизоров, поступающих в продажу. Цех 1 выпускает 5% бракованных телевизоров, цех 2 - 7%. а) Найти вероятность приобрести бракованный телевизор; б) найти вероятность того, что купленный телевизор выпущен цехом 1, если он оказался с браком.
7. Всхожесть (вероятность всхода) семян, полученных на селекционной станции 1 равна 0,9, на станции 2 - 0,8. В продажу поступает равное количество семян от обеих станций. а) Найти всхожесть приобретенных семян; б) Наугад выбранное семя при посеве не взошло. Какова вероятность его выращивания на станции 1?
|
|
|
8. Два цеха поставляют одинаковое количество болтов на сборку. Доля брака в первом цехе - 0,1, во втором - 0,2. а) Найти вероятность того, что наугад взятый на сборку болт - бракованный; б) болт оказался бракованным. Какова вероятность, что он изготовлен цехом 2?
9. Скрытый период болезни может быть длительным в 30% случаев заболевания и коротким - в 70% случаев. Вероятности выздоровления равны 0,9 для длительного и 0,6 - для краткого периодов. а) Найти вероятность выздоровления наугад выбранного больного; б) найти вероятность того, что скрытый период был длительным, если больной выздоровел.
10. По статистическим данным среди заболевающих в течение года телят 20% заболевают в теплое время и 80%- в холодное время года. Вероятность выздоровления теленка, заболевшего в теплое время года - 0,9, в холодное - 0,8. а) Найти вероятность выздоровления наугад отобранного больного; б) найти вероятность того, что теленок заболел в теплое время, если он выздоровел.
11. Блок комплектуется резистором с одного из трех заводов, осуществляющих 60%, 30% и 20% поставок. Доля брака среди резисторов составляет 0,3 на заводе 1, 0,2 - на заводе 2, 0,1- на заводе 3. А) Найти вероятность брака выпущенного блока; б) найти вероятность того, что бракованный блок укомплектован резистором завода 1.
12. В кризисной стадии болезнь может перейти с равной вероятностью в скоротечную (С) и вялотекущую (В) формы. Вероятности выздоровления равны 0,95 для формы С и 0,8 - для формы В. а) Найти вероятность выздоровления случайно выбранного больного; б) найти вероятность того, что болезнь перешла в форму С, если больной выздоровел.
13. При заболевании данной болезнью одинаково часто обнаруживаются формы А и Б, определяющие ее дальнейшее течение. В случае А больной выздоравливает в течение месяца с вероятностью 0,8, в случае Б - с вероятностью 0,6. а) Найти вероятность выздоровления за месяц случайно отобранного больного; б) найти вероятность протекании болезни в форме А, если больной выздоровел в течении месяца.
14. Вероятность выполнением плана траулером при своевременном приходе танкера-заправщика равна 0,8, при несвоевременном - 0,4. Танкер прибывает своевременно в 90% случаев. а) Найти вероятность выполнения плана траулером; б) вычислить вероятность своевременной заправки, если известно, что траулер выполнил план.
15. Лето может оказаться засушливым в 20% случаев, чрезмерно влажным в 30% случаев и нормальным в остальных случаях. Вероятности вызревания урожая составляют 0,7, 0,6 и 0,9 соответственно. а) Найти вероятность вызревания урожая в случайно выбранный год; б) найти вероятность того, что лето было засушливым, если урожай вызрел.
|
|
|
16. В данной местности встречаются лишь болезни А и Б, симптомы которых внешне неотличимы. Среди больных А встречается в 30% случаев, Б - в 70%. Вероятности выздоровления при заболеваниях равны 0,6 и 0,3 соответственно. а)найти вероятность того, что случайно взятый больной выздоровеет; б) с какой вероятностью выздоровевший болел болезнью А?
17. Объект может быть сдан в эксплуатацию в срок при плановой поставке оборудования с вероятностью 0,9, при поставке с задержкой - с вероятностью 0,6. Плановые поставки в среднем наблюдались в 80% заказов, поставки с задержкой - в 20%. а) Какова вероятность сдачи объекта в срок? б) найти вероятность своевременной поставки, если известно, что объект сдан в срок.
18. Ядерная реакция может порождать частицы типа А в 70% случаев и типа Б - в 30% случаев. Частицы А регистрируются прибором с вероятностью 0,8, частицы Б - с вероятностью 1. а) Найти вероятность регистрации частицы в предстоящем опыте; б) Прибор отметил появление частицы. С какой вероятностью она принадлежала к типу Б?
19. Среди родившихся в первом полугодии детей средний вес превышают 60% новорожденных, во втором полугодии - 30%. Считая, что рождаемость в обоих полугодиях одинакова, найти: а) вероятность превышения веса случайно выбранным ребенком; б) вероятность рождения ребёнка в первом полугодии, если он - повышенного веса.
20. Испускаемый катодом электрон может оказаться "быстрым" с вероятностью 0,7 и "медленным" - с вероятностью 0,3. Вероятность попадания в мишень "быстрых" электронов равна 0,9, "медленных" - 0,4. Найти вероятность того, что: а) электрон попадет в мишень; б) электрон был "медленным", если он достиг мишени.
21. Лисица преследуя серого зайца нагоняет его в 30% случаев, белого зайца - в 20% случаев. Оба вида зайцев встречаются в лесу с одинаковой частотой. а) Какова вероятность, что лисица догонит случайно встреченного зайца; б) найти вероятность того, что настигнутый заяц был серым.
22. Вероятность опоздания самолёта при неблагоприятных условиях (непогода, технические причины) равна 0,6 и при благоприятных условиях - 0,1. Неблагоприятные условия наблюдались в 20 % рейсов, благоприятные - в 80 %. Найти вероятность того, что: а) в следующем рейсе самолёт опоздает; б) опоздание сопровождалось неблагоприятными условиями.
23. Однотипные изделия поступают в продажу с заводов 1 и 2, поставляющих 60% и 40% изделий. Доля брака на заводе 1 равна 0,05, на заводе 2 - 0,07. Найти вероятность того, что: а) приобретенное изделие окажется бракованным; б) бракованное изделие выпущено заводом 2.
24. Две партии содержат одинаковое количество однотипных деталей и имеют доли брака (вероятности брака детали) равные 0,1 и 0,2 соответственно. Наугад выбирается одна из партий, из которой извлекается деталь. а) Найти вероятность того, что она бракованная; б) Найти вероятность того, что оказавшаяся бракованной деталь принадлежала первой партии.
25..Вероятности поражения цели бомбардировщиком при ясной погоде равна 0,9, при непогоде - 0,7. Ясная погода 1 июня наблюдалась в 60% случаев, непогода - в 40%. Найти вероятность того, что 1 июня: а) цель будет поражена; б) погода была ясная, если известно, что цель поражена.
26. Два шахматиста А и Б играют одну партию. Вероятность выигрыша А при наличии у него белых фигур равна 0,7, при наличии чёрных фигур - 0,4. Цвет фигур определяется перед партией с помощью жеребьёвки. Найти вероятность того, что: а) шахматист А выиграет; б) А играл чёрными фигурами, если известно, что он выиграл.
27. Вероятность своевременного прибытия судна при безотказной работе двигателя равна 0,8 и при его поломке - 0,1. Двигатель ранее работал безотказно в 90% рейсов судна. Найти вероятность того, что: а) в следующем рейсе судно не опоздает; б) поломки двигателя, если известно, что судно опоздало.
28. Прибор может эксплуатироваться в 30% случаев в тяжелых условиях, где он выходит из строя с вероятностью 0,3 и в 70% случаев - в благоприятных условиях, где он отказывает с вероятностью 0,1. Найти вероятность того, что: а) прибор откажет; б) отказавший прибор эксплуатировался в неблагоприятных условиях.
29. Из урны, содержащей 3 белых и 2 черных шара, по очереди извлекаются 2 шара. Цвет первого из них неизвестен. Найти вероятность того, что: а) второй шар будет белым; б) первый шар был черным, если второй оказался белым.
30. Два цеха поставляют на сборку изделия однотипные узлы. Первый из них поставляет 60% всех узлов, второй - 40%. Вероятность узла оказаться бракованным равна 0,2 для цеха 1 и 0,3 - для цеха 2. Найти вероятность того, что: а) случайно выбранный узел окажется бракованным; б) бракованный узел поступил из цеха 1.
Задание 7.3.
Построить ряд распределения, функцию распределения и ее график, найти математическое ожидание и дисперсию случайной величины X - числа наступлений случайного события А в указанной ниже серии независимых испытаний.
1. Монета подбрасывается 4 раза. А - выпадение герба при одном бросании, Р(А)=0,5.
2. Стрелок стреляет по мишени 3 раза. А - попадание при одном выстреле, Р(А)=0,6.
3. Рыболов трижды забрасывает удочку. А - поклевка при одном забрасывании, Р(А)=0,3.
4. Из урны, содержащей 2 белых и 3 черных шара, извлекается наугад шар (если он белый, то наступило А), который затем возвращается в урну. Опыт повторяется 3 раза.
5. Высеиваются 3 семечка тыквы. Всхожесть (вероятность всхода А одного семени) равна Р(А)=0,8.
6. Элементарная частица может быть зарегистрирована прибором (событие А) с вероятностью Р(А)=0,7. Перед прибором поочередно пролетают три частицы.
7. А -событие, наступающее, когда первая цифра номера встречного автомобиля - нуль. Мимо поочередно проезжают два автомобиля.
8. А - выход из строя электрооборудования автомобиля в течение года, Р(А)=0,3. Рассматриваются три автомобиля.
9. А - событие, состоящее в побитии мирового рекорда спортсменом, Р(А)=0,2. В соревновании участвуют три спортсмена.
10. Орудие выпускает по цели три снаряда. А - попадание снаряда, Р(А)=0,8.
11. Извлеченная наугад с книжной полки книга может оказаться учебником (событие А) с вероятностью Р(А)=0,4. Извлекается три книги.
12. Позитрон при рождении может приобрести правую (событие А) или левую ориентацию вращения, Р(А)=0,6. Рассматриваются 3 позитрона.
13. Наличие синей глины указывает на возможность алмазного месторождения (событие А) с вероятностью Р(А)=0,4. Синяя глина обнаружена в трех районах.
14. В период цветения растение может быть опылено (событие А) с вероятностью Р(А)=0,8. Рассматриваются 4 растения.
15. Рыболов может поймать рыбу при поклевке (событие А) с вероятностью Р(А)=0,4. У рыболова было три поклевки.
16. В ядерной реакции может образоваться резонансная частица (событие А) с вероятностью Р(А)=0,2. Рассматриваются три реакции.
17. Помещенный в грунт саженец может приняться (событие А) с вероятностью Р(А)=0,7. Высажено три саженца.
18. Генератор электростанции в течение года может выйти из строя (событие А) с вероятностью Р(А)=0,2. Рассматривается трехлетний период эксплуатации генератора.
19. В течение суток молоко в горшке может прокиснуть (событие А) с вероятностью Р(А)=0,4. Рассматривается случай трех горшков.
20. На фотографии, полученной в камере Вильсона частица регистрируется в опыте (событие А) с вероятностью Р(А)=0,5. Проведено 4 опыта.
21. А - появление четного числа очков при бросании игральной кости. Кость выбрасывается 4 раза.
22. Три орудия стреляют по своим целям, А - попадание снаряда в цель, Р(А)=0,7.
23. Рыболов при поклевке может вытащить рыбу (событие А) с вероятностью Р(А)=0,6. Поклевка произошла у 4 рыболовов.
24. Биение ротора электродвигателя приводит к его выходу из строя в вероятностью Р(А)=0,8. Рассматриваются три однотипных двигателя.
25. При изготовлении детали она может оказаться бракованной (событие А) с вероятностью Р(А)=0,2. Изготовлено три детали.
26. Станок работает безотказно в течение года (событие А) с вероятностью Р(А)=0,8. В цехе работают 4 станка.
27. А - появление нечетного числа очков при бросании игральной кости. Кость выбрасывается 4 раза.
28. Поезд может прибыть по расписанию (событие А) с вероятностью Р(А)=0,9. Рассматриваются три рейса.
29. В среднем при наборе страницы текста оператор совершает ошибку (событие А) в 30% случаев. Статья содержит 4 страницы текста.
30. Самолет-разведчик может обнаружить цель (событие А) с вероятностью Р(А)=0,8. Для обнаружения цели послано три самолета.
Задание 7.4.
По заданной функции распределения F(x) случайной величины СВ X найти плотность распределения и построить ее график. Вычислить вероятность P(a ≤X≤ b) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 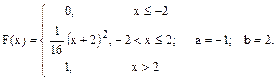
14. 
15. 
16. 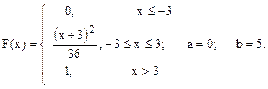
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 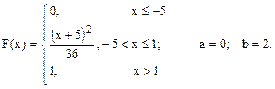
30. 
Задание 7.5.
Найти вероятность попадания в заданный интервал [ a,b ] значения нормально распределенной случайной величины X, если известно её математическое ожидание M [ X ] и дисперсия D [ X ].
| Вар. | M [ X ] | D [ X ] | 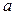
| b |
| 1 | 10 | 16 | 2 | 13 |
| 2 | 9 | 25 | 5 | 14 |
| 3 | 8 | 1 | 6 | 9 |
| 4 | 7 | 4 | 3 | 10 |
| 5 | 6 | 9 | 2 | 11 |
| 6 | 5 | 1 | 5 | 7 |
| 7 | 4 | 25 | 2 | 7 |
| 8 | 3 | 4 | 3 | 10 |
| 9 | 2 | 25 | 4 | 9 |
| 10 | 2 | 16 | 6 | 10 |
| 11 | 10 | 4 | 9 | 12 |
| 12 | 9 | 16 | 5 | 12 |
| 13 | 8 | 4 | 4 | 10 |
| 14 | 7 | 9 | 4 | 11 |
| 15 | 6 | 4 | 3 | 10 |
| 16 | 5 | 4 | 2 | 7 |
| 17 | 3 | 1 | 2 | 5 |
| 18 | 4 | 1 | 3 | 7 |
| 19 | 2 | 9 | -2 | 4 |
| 20 | 0 | 16 | -1 | 3 |
| 21 | 5 | 9 | 4 | 9 |
| 22 | 6 | 4 | 4 | 10 |
| 23 | 8 | 9 | 0 | 9 |
| 24 | 7 | 16 | -1 | 20 |
| 25 | -8 | 9 | -9 | 0 |
| 26 | 2 | 9 | -2 | 4 |
| 27 | 7 | 36 | 0 | 9 |
| 28 | 8 | 25 | 2 | 10 |
| 29 | 1 | 9 | -1 | 5 |
| 30 | 4 | 9 | 0 | 9 |
Задание 7.6.
В партии из n изделий каждое может оказаться стандартным с вероятностью p. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет: а) равно m; б) заключено между m 1 и m 2.
| Вар. | p | n | m | m1 | m2 |
| 1 | 0.3 | 100 | 32 | 25 | 35 |
| 2 | 0,7 | 400 | 287 | 270 | 290 |
| 3 | 0,5 | 300 | 143 | 145 | 160 |
| 4 | 0,4 | 350 | 137 | 135 | 155 |
| 5 | 0,6 | 600 | 365 | 340 | 365 |
| 6 | 0,2 | 850 | 166 | 145 | 185 |
| 7 | 0,4 | 900 | 362 | 340 | 375 |
| 8 | 0,6 | 750 | 447 | 435 | 470 |
| 9 | 0,3 | 150 | 47 | 40 | 55 |
| 10 | 0,8 | 100 | 76 | 75 | 90 |
| 11 | 0,3 | 400 | 116 | 100 | 130 |
| 12 | 0,7 | 200 | 145 | 130 | 150 |
| 13 | 0,2 | 450 | 86 | 80 | 95 |
| 14 | 0,1 | 900 | 96 | 80 | 100 |
| 15 | 0,5 | 750 | 381 | 355 | 385 |
| 16 | 0,4 | 750 | 294 | 285 | 320 |
| 17 | 0,6 | 200 | 125 | 110 | 135 |
| 18 | 0,2 | 600 | 112 | 105 | 135 |
| 19 | 0,3 | 400 | 127 | 110 | 130 |
| 20 | 0,1 | 700 | 64 | 55 | 80 |
| 21 | 0,7 | 650 | 450 | 445 | 480 |
| 22 | 0,5 | 300 | 155 | 140 | 160 |
| 23 | 0,6 | 450 | 262 | 255 | 280 |
| 24 | 0,8 | 200 | 163 | 145 | 165 |
| 25 | 0,1 | 400 | 44 | 35 | 55 |
| 26 | 0,3 | 500 | 147 | 130 | 165 |
| 27 | 0,2 | 200 | 43 | 30 | 50 |
| 28 | 0,4 | 650 | 250 | 245 | 270 |
| 29 | 0,6 | 300 | 185 | 175 | 195 |
| 30 | 0,5 | 500 | 243 | 235 | 265 |
Задание 7.7.
Двумерная случайная величина (X,Y) имеет плотность распределения
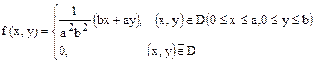
Найти вероятность попадания значения (X,Y) в область 
 вероятность попадания значения X в интервал
вероятность попадания значения X в интервал  математическое ожидание M [ X ] и условное математическое ожидание
математическое ожидание M [ X ] и условное математическое ожидание 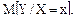
| Вар | a | b | x1 | x2 | y1 | y2 |
| 1 | 4 | 2 | 3 | 6 | -2 | 1 |
| 2 | 8 | 2 | 6 | 9 | 0 | 4 |
| 3 | 6 | 4 | 3 | 7 | 2 | 3 |
| 4 | 5 | 3 | 2 | 4 | -4 | 1 |
| 5 | 9 | 4 | -4 | 6 | 1 | 5 |
| 6 | 3 | 5 | 1 | 2 | 4 | 7 |
| 7 | 2 | 6 | 3 | 8 | -2 | 4 |
| 8 | 7 | 4 | -1 | 5 | 2 | 6 |
| 9 | 5 | 6 | -3 | 2 | 4 | 7 |
| 10 | 4 | 7 | 1 | 6 | -2 | 5 |
| 11 | 6 | 3 | 0 | 4 | -1 | 2 |
| 12 | 8 | 4 | 2 | 6 | 3 | 7 |
| 13 | 3 | 4 | -2 | 2 | 1 | 5 |
| 14 | 7 | 2 | -4 | 3 | 0 | 5 |
| 15 | 6 | 5 | 2 | 7 | -3 | 4 |
| 16 | 2 | 4 | -2 | 1 | 3 | 6 |
| 17 | 2 | 8 | 0 | 4 | 6 | 9 |
| 18 | 4 | 6 | 2 | 3 | 3 | 7 |
| 19 | 3 | 5 | -4 | 1 | 2 | 4 |
| 20 | 4 | 9 | 1 | 5 | -4 | 6 |
| 21 | 5 | 3 | 4 | 7 | 1 | 2 |
| 22 | 6 | 2 | -2 | 4 | 3 | 8 |
| 23 | 4 | 7 | 2 | 6 | -1 | 5 |
| 24 | 6 | 5 | 4 | 7 | -3 | 2 |
| 25 | 7 | 4 | -2 | 5 | 1 | 6 |
| 26 | 3 | 6 | -1 | 2 | 0 | 4 |
| 27 | 4 | 8 | 3 | 7 | 2 | 6 |
| 28 | 4 | 3 | 1 | 5 | -2 | 2 |
| 29 | 2 | 7 | 0 | 5 | -4 | 3 |
| 30 | 5 | 6 | -3 | 4 | 2 | 7 |
Задание 7.8.
Случайная величина Х имеет плотность распределения f (x). Для случайной величины Y = j (X) найти плотность распределения g (y), вероятность P (a £ Y £ b), математическое ожидание M [ Y ] и дисперсию D [ Y ].
1. 
2. 
3. 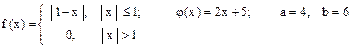
4. 
5. 
6. 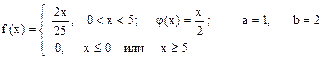
7. 
8. 
9. 
10. 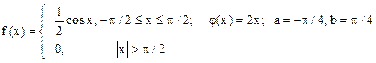
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 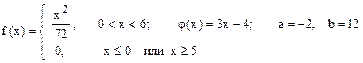
19. 
20. 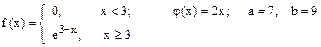
21. 
22. 
23. 
24. 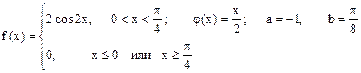
25. 
26. 
27. 
28. 
29. 
30. 
Задание 7.9.
Задана матрица перехода системы из состояния i (i =1,2) в состояние j (j =1,2) за один шаг  . Найти матрицу перехода из состояния i в состояние j за два шага.
. Найти матрицу перехода из состояния i в состояние j за два шага.
| Вар. | a | b | C | D |
| 1 | 0,1 | 0,9 | 0,2 | 0,8 |
| 2 | 0,2 | 0,8 | 0,7 | 0,3 |
| 3 | 0,3 | 0,7 | 0,4 | 0,6 |
| 4 | 0,4 | 0,6 | 0,5 | 0,5 |
| 5 | 0,6 | 0,4 | 0,7 | 0,3 |
| 6 | 0,6 | 0,4 | 0,8 | 0,2 |
| 7 | 0,8 | 0,2 | 0,9 | 0,1 |
| 8 | 0,8 | 0,2 | 0,2 | 0,8 |
| 9 | 0,9 | 0,1 | 0,2 | 0,8 |
| 10 | 0,4 | 0,6 | 0,1 | 0,9 |
| 11 | 0,7 | 0,3 | 0,2 | 0,8 |
| 12 | 0,5 | 0,5 | 0,4 | 0,6 |
| 13 | 0,3 | 0,7 | 0,2 | 0,8 |
| 14 | 0,2 | 0,8 | 0,5 | 0,5 |
| 15 | 0,9 | 0,1 | 0,7 | 0,3 |
| 16 | 0,9 | 0,1 | 0,8 | 0,2 |
| 17 | 0,8 | 0,2 | 0,3 | 0,7 |
| 18 | 0,4 | 0,6 | 0,3 | 0,7 |
| 19 | 0,5 | 0,5 | 0,4 | 0,6 |
| 20 | 0,3 | 0,7 | 0,6 | 0,4 |
| 21 | 0,8 | 0,2 | 0,4 | 0,6 |
| 22 | 0,2 | 0,8 | 0,5 | 0,5 |
| 23 | 0,2 | 0,8 | 0,1 | 0,9 |
| 24 | 0,4 | 0,6 | 0,7 | 0,3 |
| 25 | 0,1 | 0,9 | 0,4 | 0,6 |
| 26 | 0,2 | 0,8 | 0,7 | 0,3 |
| 27 | 0,4 | 0,6 | 0,5 | 0,5 |
| 28 | 0,2 | 0,8 | 0,2 | 0,8 |
| 29 | 0,5 | 0,5 | 0,3 | 0,7 |
| 30 | 0,7 | 0,3 | 0,9 | 0,1 |
Контрольная работа №8
"Математическая статистика"
Задание 8.1.
Из генеральной совокупности извлечена выборка, представленная в виде статистического ряда (в первой строке указаны выборочные значения 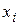 , во второй - соответствующие им частоты
, во второй - соответствующие им частоты  ). Требуется вычислить выборочное среднее
). Требуется вычислить выборочное среднее  , выборочную дисперсию DB
, выборочную дисперсию DB
|
|
|


