 |
Задание 5.5. Найти общее решение:
|
|
|
|
Это уравнение 2-ого порядка, не содержащее искомой функции 
. Оно допускает понижение порядка уравнения заменой 
, 
.
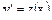После замены исходное уравнение превращается в однородное уравнение первого порядка:
.
Делаем подстановку:
, 
.
Тогда
.
Разделяем переменные:
, 
, 
;
. 
.
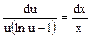Так как 
, то
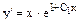
Находим:
.
Общее решение уравнения имеет вид:
.
Задание 5.6. Найти общее решение:
Это уравнение второго порядка, не содержащее независимой переменной 
. Оно допускает понижение порядка уравнения заменой:
, 
После замены, исходное уравнение преобразуется в уравнение с разделяющимися переменными:
Решаем это уравнение:
, 
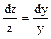Так как 
, то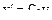 
.
Снова получили уравнение с разделяющимися переменными, поэтому
, 
.
Значит, 
— общее решение нашего уравнения.
Задание 5.7. Решить задачу Коши:
, 
, 
, 
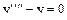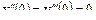
Составляем характеристическое уравнение и решаем его:
, 
, 
, 
, 
.
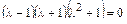Общее решение исходного уравнения имеет вид:
.
Находим:
.
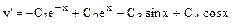
Используем начальные условия
Решаем систему:
, 
, 
, 
.
Решение задачи Коши имеет вид:
.
Задание 5.8. Найти общее решение:
.
Находим корни характеристического уравнения:
Следовательно общее решение однородного уравнения имеет вид
(
; 
— фундаментальная система решений):
.
Правая часть уравнения представляет собой сумму функци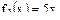й 
и 
.
Для нахождения частных решений, соответствующих этим функциям составляем:
для 
S=1 (кратность числа 
среди корней характеристического уравнения)
|
|
|
;
для 
:
(кратность числа 
среди корней характеристического уравнения).
т.е. 
— частное решение нелинейного уравнения с неизвестными коэффициентами.
Подставляем 
в исходное уравнение:
Для выполнения тождества необходимо равенство коэффициентов:
Поэтому: 
Таким образом, частное решение исходного уравнения имеет вид:
,
а его общее решение:
Задание 5.9. Найти общее решение:
Находим общее решение однородного уравнения:
Частное решение неоднородного уравнения по методу Лагранжа имеет вид:
Для нахождения функций 
составляем систему:
Тогда:
Таким образом, общим решением уравнения является функция: 
Здесь Ai, Bi (i =1, 2, 3).
Задание 5.10. Методом исключения найти общее решение системы:
Первое уравнение продифференцируем по 
:
Из второго уравнения подставим в полученное выражение 
:
Из первого выразим 
и подставим его в последнее уравнение:
Окончательно получим:
Решаем это уравнение:
; 
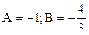
Из выражения для 
получим:
Таким образом, общее решение системы имеет вид:
.
Задание 5.11. а) Методом характеристического уравнения найти общее решение системы:
Составляем характеристическое уравнение и решаем его:
Для 
составляем систему:
Пусть 
тогда 
и
Для 
:
.
Пусть 
, тогда 
и
.
Общим решением исходной системы будет вектор функция:
или в координатной форме:
б) С помощью операционного исчисления найти общее решение системы:
Применим преобразование Лапласа к обеим частям каждого уравнения:
|
|
|
Пользуясь свойством линейности преобразования и теоремой о дифференцировании оригинала:
получим:
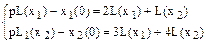
Т. к. 
и 
не заданы, то считаем их произвольными величинами:
Тогда
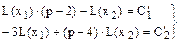
Откуда
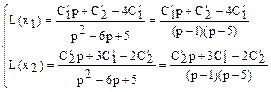
Для восстановления оригиналов 
и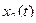 
разложим дроби на простейшие:
Тогда
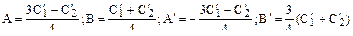
Поскольку 
и 
— произвольные, то можно ввести обозначения:
Поэтому: 
Так как для изображения 
оригиналом является 
, то получаем общее решение системы:
Решение типового варианта
Контрольной работы N6.
Задание 6.1. Исследовать сходимость числового ряда 
.
Решение: Воспользуемся признаком Д'Аламбера:
, 
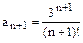
Следовательно, ряд сходится.
Задание 6.2. Исследовать сходимость числового ряда 
.
Решение. Применим радикальный признак Коши: 
, 
, т.о. ряд расходится.
Задание 6.3. Исследовать сходимость числового ряда 
.
Решение. Применим интегральный признак Коши. Функция 
удовлетворяет условиям признака. Исследуем несобственный интеграл 
. Т.к. интеграл сходится, то сходится и данный ряд.
|
|
|
