 |
Задание 6.4. Исследовать сходимость числового ряда
|
|
|
|
 .
.
Решение. Воспользуемся предельным признаком сравнения.
Сравним данный ряд и ряд 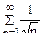 , который расходится.
, который расходится. 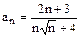 ,
, 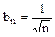 .
.
 . Значит, исследуемый ряд расходится, так же как и ряд
. Значит, исследуемый ряд расходится, так же как и ряд 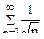 .
.
Задание 6.5. Исследовать сходимость числового ряда  .
.
Решение.  . Ряд расходится, т.к.
. Ряд расходится, т.к.
не выполняется необходимый признак сходимости рядов 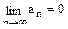 .
.
Задание 6.6. Исследовать на сходимость, абсолютную и условную знакочередующийся ряд 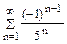 .
.
Решение. Данный знакочередующийся ряд сходится по признаку Лейбница,
т.к. 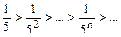 и
и 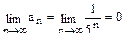 . Этот ряд сходится абсолютно, т.к. ряд из абсолютных величин его членов
. Этот ряд сходится абсолютно, т.к. ряд из абсолютных величин его членов  сходится по признаку Коши, т.к.
сходится по признаку Коши, т.к. 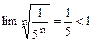 .
.
Задание 6.7. Исследовать на сходимость, условную или абсолютную сходимость знакочередующийся ряд 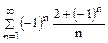 .
.
Решение. Представим данный ряд в виде суммы двух рядов 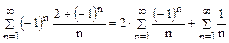 . Для ряда
. Для ряда 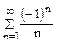 выполняется
выполняется
признак Лейбница 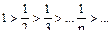 и
и 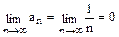 , т.е. ряд сходится. Т.к. ряд
, т.е. ряд сходится. Т.к. ряд 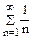 , составленный из абсолютных величин ряда
, составленный из абсолютных величин ряда 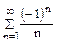 , есть гармонический ряд (расходящийся), то ряд
, есть гармонический ряд (расходящийся), то ряд 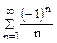 сходится условно. Исходный ряд
сходится условно. Исходный ряд 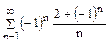 как сумма сходящегося условно ряда
как сумма сходящегося условно ряда 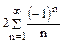 и расходящегося ряда
и расходящегося ряда 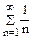 , расходится.
, расходится.
Задание 6.8. Найти область сходимости степенного ряда 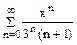 .
.
Решение. Для данного степенного ряда вида 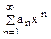 ,
, 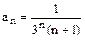 ,
, 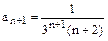 .
.
Радиус сходимости 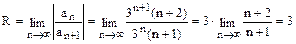 . Следовательно, ряд сходится в интервале (-3; 3). Исследуем сходимость ряда на концах интервала. Положим сначала x = 3.
. Следовательно, ряд сходится в интервале (-3; 3). Исследуем сходимость ряда на концах интервала. Положим сначала x = 3.
Получим числовой ряд 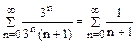 , который расходится (сравним с гармоническим рядом
, который расходится (сравним с гармоническим рядом 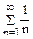 ). Возьмем теперь x = -3. Получим знакочередующийся ряд
). Возьмем теперь x = -3. Получим знакочередующийся ряд 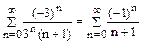 , который сходится условно по признаку Лейбница
, который сходится условно по признаку Лейбница
(см. решение примера 6.7.). Таким образом, область сходимости ряда - полуинтервал 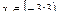 .
.
Задание 6.9. Найти область сходимости степенного ряда 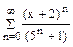 .
.
Решение. Для данного степенного ряда вида  ,
, 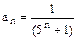 ,
, 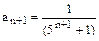 , x0 = -2. Определим радиус сходимости ряда
, x0 = -2. Определим радиус сходимости ряда 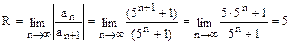 . Таким образом, ряд сходится в интервале (x0 - R, x0 + R), т.е. (-2-5;-2+5) или (-7;3). Исследуем сходимость ряда на концах интервала. Возьмем x=3. Получим числовой ряд
. Таким образом, ряд сходится в интервале (x0 - R, x0 + R), т.е. (-2-5;-2+5) или (-7;3). Исследуем сходимость ряда на концах интервала. Возьмем x=3. Получим числовой ряд  .
.
|
|
|
Предел общего члена этого ряда  , следовательно, ряд расходится. При x = -7 получим знакочередующийся ряд
, следовательно, ряд расходится. При x = -7 получим знакочередующийся ряд 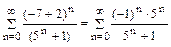 , для которого не выполняется признак сходимости Лейбница
, для которого не выполняется признак сходимости Лейбница  . Значит, и при x = -7 данный степенной ряд расходится. Таким образом, исходный степенной ряд сходится в интервале
. Значит, и при x = -7 данный степенной ряд расходится. Таким образом, исходный степенной ряд сходится в интервале  .
.
Замечание. Область сходимости степенного ряда можно находить и как для произвольного функционального ряда 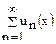 . В этом примере
. В этом примере 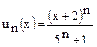 . По признаку Д'аламбера
. По признаку Д'аламбера
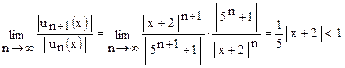 . Отсюда
. Отсюда 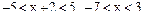 . Далее, как и выше, последует сходимость в точках
. Далее, как и выше, последует сходимость в точках  и
и 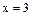 .
.
Задание 6.10. Разложить в ряд Тейлора функцию 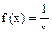 в окрестности точки
в окрестности точки  . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда.
Решение. Искомое разложение можно найти с помощью формулы 
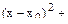
 ,
,
положив в ней  и вычислив значения производных функции
и вычислив значения производных функции 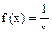 при
при  . Но проще получить разложение, используя известное разложение для функции
. Но проще получить разложение, используя известное разложение для функции
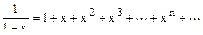 ,
,
в котором ряд справа сходится к функции 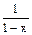 в интервале (-1,1).
в интервале (-1,1).
Представим  . Применяя указанное разложение, получим
. Применяя указанное разложение, получим
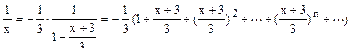 .
.
Так как, ряд, который использовали для разложения, сходится для 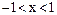 , то данный ряд сходится для
, то данный ряд сходится для 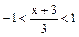 , отсюда
, отсюда 
 . Таким образом, полученный степенной ряд является рядом Тейлора функции
. Таким образом, полученный степенной ряд является рядом Тейлора функции 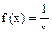 в окрестности точки
в окрестности точки  и его областью сходимости является интервал (-6,0).
и его областью сходимости является интервал (-6,0).
Задание 6.11. Используя разложение подынтегральной функции в степенной ряд, вычислить определенный интеграл 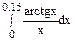 с точностью до 0.001.
с точностью до 0.001.
Решение. Воспользуемся рядом Маклорена для 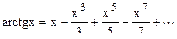 , тогда
, тогда 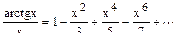 .
.
Почленно интегрируя этот ряд в промежутке [0;0.5], получим
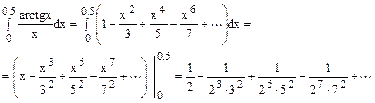
Полученный числовой ряд есть ряд Лейбница. Погрешность, происходящая от отбрасывания всех членов ряда, начиная с четвертого 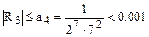 , поэтому, чтобы достичь требуемой точности достаточно взять три первых слагаемых
, поэтому, чтобы достичь требуемой точности достаточно взять три первых слагаемых 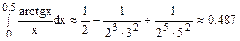
Задание 6.12. Разложить в ряд Фурье периодическую с периодом 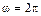 функцию
функцию
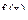 =
= 

|
|
|
Решение. Вычислим коэффициенты Фурье:

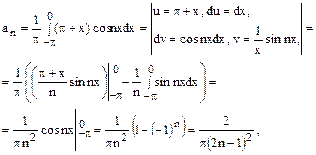

Ряд Фурье для данной функции запишется в виде

Задание 6.13. Разложить в ряд Фурье функцию 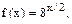 заданную в интервале (0;
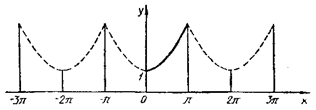
заданную в интервале (0;  ), продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения.
), продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения.
Решение. Продолжим данную функцию четным образом. Тогда:
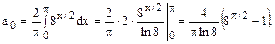

Найдем неопределенный интеграл 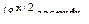 выполнив дважды интегрирование по частям:
выполнив дважды интегрирование по частям:

Вычислим коэффициенты 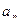 :
:

Следовательно, разложение данной функции по косинусам имеет вид:
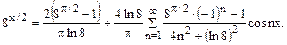
Теперь продолжим данную функцию нечетным образом. Тогда:
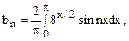


Следовательно, разложение данной функции по синусам имеет вид:

Задание 6.14. Разложить в ряд Фурье периодическую (с периодом  ) функцию
) функцию
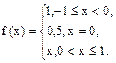
Решение. Вычисляем коэффициенты 
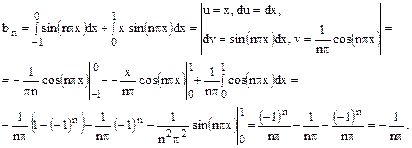
В итоге получаем следующий ряд Фурье:
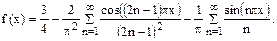
Задание 6.15. Разложить в ряд Фурье по косинусам функцию
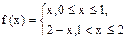
на отрезке [0;2] и найти сумму ряда 
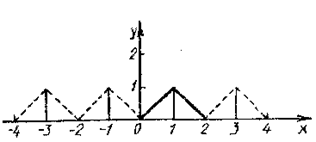
Решение. Продолжим функцию четным образом и вычислим коэффициенты Фурье:

Следовательно,
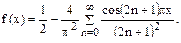
Полагая 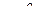 получаем:
получаем:
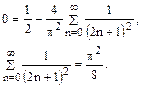
Таким образом, с помощью ряда Фурье мы нашли сумму числового ряда.
Решение типового варианта
Контрольной работы № 7
Задание 7.1. Для доставки экстренного сообщения отправлены различными маршрутами два курьера. Вероятности своевременной доставки сообщения курьерами равны 0,8 и 0,6 соответственно. Найти вероятности того, что:
а) своевременно успеют оба курьера; б) только один курьер;
в) хотя бы один курьер; г) оба курьера опоздают.
Решение. Обозначим через A, B случайные события, наступающие в случаях, когда успевают первый или второй курьеры соответственно, р(А)=0,8, р(В)=0,6. Введем также события: С - успевают оба курьера, D - только один курьер, Е - хотя бы один курьер, F - оба курьера опоздают.
а) Представим событие в виде С=А·В. Применяя теорему умножения вероятностей и учитывая очевидную из условия независимость событий А, В находим
Р(С) = Р(А · В) = Р(А) · Р(В) = 0,8 · 0,6
б) Согласно условию D=А· 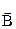 +
+ 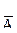 ·В (чертой обозначены противоположные события). По теореме сложения вероятностей с учетом несовместности слагаемых имеем
·В (чертой обозначены противоположные события). По теореме сложения вероятностей с учетом несовместности слагаемых имеем
|
|
|
Р(D) = P(А·  +
+ 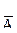 ·В) = P(А·
·В) = P(А· 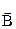 ) + P(
) + P(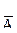 ·В)
·В)
Вновь применяя теорему умножения при независимых сомножителях находим
P(D) = P(A)·P(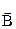 ) + P(
) + P(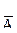 )·P(B) = P(A) · (1- P(B)) + (1- P(A)) · P(B) =
)·P(B) = P(A) · (1- P(B)) + (1- P(A)) · P(B) =
= 0,8(1-0,6) + (1-0,8) = 0,28.
в) Здесь D = A + B. Слагаемые А, В совместны, поэтому теорема сложения запишется
P(D) = P(A+B) = P(A) + P(B) - P(A·B) = P(A) + (B) - P(A) · P(B) = 0,8+0,6-0,8·0,6 = 0,92.
г) По условию F = 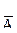 ·
· 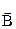 , откуда P(F) = P(
, откуда P(F) = P(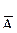 ·
· 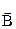 ) = P(
) = P(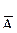 ) · P(
) · P(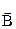 ) = (1-P(A))(1-P(B)) =0,2 · 0,4 = 0,08.
) = (1-P(A))(1-P(B)) =0,2 · 0,4 = 0,08.
Заметим также, что события D + F является достоверным, поэтому P(D + F) = 1. Поскольку D, F несовместны, то P(D + F) = P(D) + P(F), откуда можно также найти вероятность P(F) = 1- P(D) = 0,08.
Задание 7.2. На сборку телевизоров поступают однотипные кинескопы от двух заводов, поставляющих соответственно 60% и 40% кинескопов. Вероятность для кинескопа оказаться нестандартным равна: 0,1 - на первом заводе, 0,2 - на втором. Найти вероятность того, что:
а) очередной на сборке кинескоп будет нестандартным;
б) оказавшийся нестандартным кинескоп изготовлен вторым заводом.
Решение. Обозначим через Нi (i = 1,2) гипотезу - кинескоп изготовлен i-тым заводом. Очевидно, что Н1, Н2 несовместны и Н1 + Н2 = I - достоверное событие. Из условия видно также, что Р(Н1) = 0,6, Р(Н2) = 0,4. Обозначим через А событие: очередной кинескоп окажется нестандартным.
а) По формуле полной вероятности имеем: Р(А) = Р(А / Н1) · Р(Н1) + Р(А / Н2) · Р(Н2).
Согласно условию Р(А / Н1) = 0,1, Р(А / Н2) = 0,2,
поэтому Р(А) = 0,1·0,6 + 0,2·0,4 = 0,14.
б) Для вычисления искомой вероятности Р(Н2 / А) используем формулу Байеса

Задание 7.3. Построить ряд распределения, функцию распределения и её график, и найти математическое ожидание и дисперсию случайной величины Х - числа наступлений случайного события А в указанный ниже серии независимых испытаний:
поступила партия из 3 изделий, каждое из которых может оказаться бракованным (событие А, Р(А) = 0,4).
Решение. Случайная величина (СВ)Х - число бракованных изделий - может принимать значения 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли при р = 0,4, q = 1- 0,4 = 0,6.
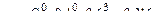 ,
, 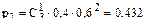 ,
,
 ,
, 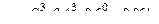
Ряд распределения СВ Х имеет вид:
|
|
|
| x i | 0 | 1 | 2 | 3 |
| pi | 0,216 | 0,432 | 0,288 | 0,064 |
Функция распределения по определению равна F(x) = P(X < x) и запишется:
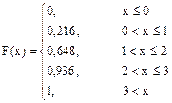
График показан на рисунке.
 F(x)
F(x)




 1
1



 0,8
0,8

 0,6
0,6


 0,4
0,4

 0,2
0,2
x



1 2 3
Вычисляем математическое ожидание и дисперсию:
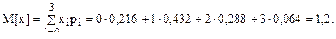

D[ x ] = 2,16 - (1,2)2 = 0,72.
Задание 7.4. По заданной функции распределения F(x) CB X найти плотность распределения и построить её график. Вычислить вероятность Р(а ≤ Х ≤ в) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.

а = -3; в = 5.
Решение. Плотность распределения определяется по формуле

и показана на рисунке
 f (x)
f (x)



 0,75
0,75




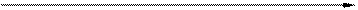

0 2 6 x
Искомая вероятность равна: 
Математическое ожидание и дисперсия запишутся:


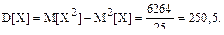
Задание 7.5. Найти вероятность попадания в заданный интервал значения нормаль-
ного распределённой СВ Х, если известно её математическое ожидание М[ x ] и дис-
персия D[x].
M[ x ] = 4; D[ x ] = 25; a = -7; в = 9.
Решение. Искомая вероятность вычисляется по формуле
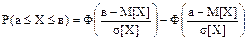
Среднеквадратическое отклонение 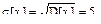 поэтому
поэтому
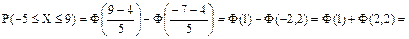
Здесь учтена нечётность вспомогательной функции 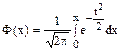
Берём её значение из таблицы: Ф(1) = , Ф(2,2) = ,
откуда Р = .
Задание 7.6. В партии из n деталей каждая может оказаться стандартной с вероятностью р. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет:
|
|
|
а) равно m; б) заключено между m 1 и m 2.
p =0,4; n = 350; m = 146; m 1 = 135; m 2 = 152.
Решение. а) Искомая вероятность при n >> 1, np >> 1 вычисляется по локальной формуле (q = 1 - p)

где вспомогательная функция имеет вид: 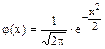 .
.
Для х = 0,66 имеем после вычислений р1 = 0,03.
б) Вероятность вычисляется с помощью интегральной формулы

откуда с помощью таблицы для Ф(х) и имеем Р2 = + =
Задание 7.7. Двумерная случайная величина (X,Y) имеет плотность распределения
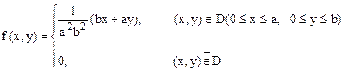
Найти вероятность попаданий значения (X,Y) в область х 1 ≤ х ≤ х 2, y 1 ≤ y ≤ y 2, вероятность попадания значения Х в интервал х 1 ≤ х ≤ х 2, математическое ожидание
М[ x ] и условное математическое ожидание M[Y/X = x ].
a = 2, в = 5, х 1 = 1, х 2 = 9, у 1 = - 4, у 2 = 3.
Решение. Найдём вероятность попадания в область S(х 1 ≤ х ≤ х 2, y 1 ≤ y ≤ y 2) по формуле Р(х 1 ≤ X ≤ х 2, y 1 ≤ Y ≤ y 2) = 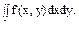
При вычислении интеграла учитывается та часть области S, где f ≠ 0,
т.е. 1 ≤ х ≤ 2, 0 ≤ у ≤ 3:
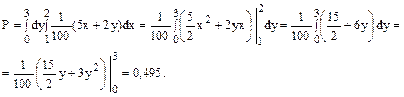
Плотность вероятности для составляющей Х имеет вид: 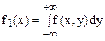 .
.
Если х < 0 или х > 2, то f (x, y) = 0 и f 1(x) = 0. При 0 ≤ х ≤ 2 находим

Таким образом плотность имеет вид:
 (1)
(1)
Тогда
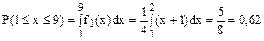

Условное математическое ожидание М[Y/X = x ] определяется с помощью услов-ной плотности распределения f 2(y / x) составляющей Y (т.е. плотности СВ Y при условии, что СВ Х приняла известное значение х):
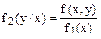 (2)
(2)
Согласно (1) СВ Х может принимать лишь значения 0 ≤ х ≤ 2, поэтому из (2), (1) и условия задачи получаем
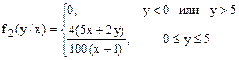
Искомое математическое ожидание равно
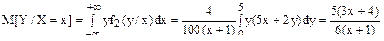 (3)
(3)
Полученная зависимость называется уравнением регрессии Y на Х.
Задание 7.8. СВ Х имеет плотность распределения. Для СВ Y = φ(Х) найти её плотность распределения g (y), вероятность P(а ≤ Y ≤ в), математическое ожидание
M[Y] и дисперсию D[Y].

Решение. Плотность распределения СВ Y = φ(x) даётся формулой
g (y) = f (ψ(y))/ψ'(y)/ (1)
где х = ψ(у) - функция, обратная к у = φ(х). В данном случае у = φ(х) = 2 х - 3,
х = ψ(у) = (у + 3)/2. Согласно и условию задачи находим
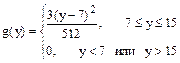
Остальные величины можно вычислить с помощью g (y) или непосредственно через f (x) по формулам
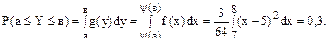

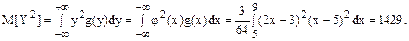
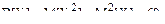
Задание 7.9. Задана матрица перехода системы из состояния i (i = 1, 2) в состояние j (j = 1, 2) за один шаг:

Найти матрицу перехода из состояния i в состояние j за два шага.
а = 0,3, в = 0,7, с = 0,8, d = 0,2
Решение. Заданная матрица имеет вид: 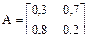
Матрица перехода i → j за n шагов равна Аn и для n = 2 запишется
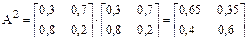
Решение типового варианта
Контрольной работы №8.
Задача 8.1.
Из генеральной совокупности извлечена выборка, представленная в виде статистического ряда (в первой строке указаны выборочные значения xi, во второй - соответствующие им частоты ni). Требуется вычислить выборочное среднее  , выборочную дисперсию Dв, исправленную выборочную дисперсию S2 и среднеквадратическое отклонение S, эмпирическую функцию распределения.
, выборочную дисперсию Dв, исправленную выборочную дисперсию S2 и среднеквадратическое отклонение S, эмпирическую функцию распределения.
| xi | 2 | 3 | 5 | 6 | 8 | 9 | 10 |
| ni | 4 | 10 | 21 | 30 | 20 | 10 | 5 |
Решение. Объём выборки равен 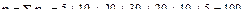 . Выборочные среднее и дисперсия вычисляются по формулам
. Выборочные среднее и дисперсия вычисляются по формулам
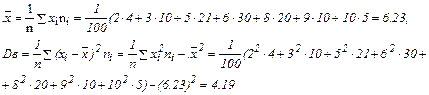
Исправленная выборочная дисперсия равна

Тогда "исправленное" выборочное среднеквадратическое отклонение будет

Согласно определению эмпирической функции распределения её значение при лю-бом x равно F*(x) = nx⁄100, где nx - количество элементов xi выборки, меньших, чем x. Например, при x=-1.3 имеем nx= 0, F*(-1.3) = 0; при x = 2.7 nx=4, F*(2.7)=4/100=0.04; при x=3.2 nx=4+10=14, F*(3.2)=0.14; при x =5.8 nx=4+10+21=35, F*(5.8)=0.35 и т.д. Тогда

Задача 8.2.
По заданным выборочному среднему  и исправленному среднеквадратическому отклонению s найти с доверительной вероятностью g доверительный интервал для математического ожидания M [Х] нормально распределённой СВ X, если: а) s[X] известно (принять s[X]=s); б) s[X] неизвестно. Построить доверительный интервал для s[X]. Число степеней свободы принять равным трём.
и исправленному среднеквадратическому отклонению s найти с доверительной вероятностью g доверительный интервал для математического ожидания M [Х] нормально распределённой СВ X, если: а) s[X] известно (принять s[X]=s); б) s[X] неизвестно. Построить доверительный интервал для s[X]. Число степеней свободы принять равным трём.
 =24.3; s =8.2; n = 150; g =0.95.
=24.3; s =8.2; n = 150; g =0.95.
Решение. а) В случае, когда среднеквадратическое отклонение (СКО) известно
(s [X]=8.2), доверительный интервал для математического ожидания можно запи-сать

где корень уравнения Φ(t) = g/2 = 0.475 отыскивается из таблицы значений функ-ции Лапласа
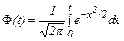
и равен t = 1.96. Вычисляя величину
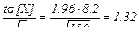
находим доверительный интервал (22.98; 25.62).
б) Если СКО неизвестно, в качестве его оценки принимается значение s (s [X] ≈ s), причём значение t определяется из таблицы распределения Стьюдента при g = 0.95 и числе степеней свободы, равном 3 (t=3.18). Тогда доверительный интервал 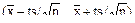 имеет вид (22.17; 26.43).
имеет вид (22.17; 26.43).
Доверительный интервал для s [X] запишется
s(1- q) < s [X] < (1 + q)
где q определяется из таблицы q = q(p, n) и для доверительной вероятности g = =0.95 и объёма выборки n=150 равно q = 0. 115. Поэтому границы интервала принимают вид
s(1-q) = 8.2(1-0.115) = 7.26, s(1+q) = 8.2(1+0.115) = 9.15,
т.е., 7.26 < s [X] < 9.15.
Задача 8.3.
1.Выборку значений СВ Х, указанную в условии задачи 8.1 сгруппировать, разбивая отрезок [a,b] (а = min хi; b = max хi) на 5 интервалов 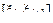 с границами
с границами

и подсчитать частоты интервалов.
2. Предполагая, что Х распределена по нормальному закону и принимая в качестве параметров М[X], s[X] их оценки 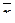 , s вычислить теоретические частоты интерва-лов.
, s вычислить теоретические частоты интерва-лов.
3. С помощью критерия согласия Пирсона при уровне значимости α =0.1 проверить, согласуются ли выборочные данные с гипотезой о нормальном распределении величины Х. Число степеней свободы принять равным трём.
Решение. 1. Из статистического ряда задачи 8.1видно, что а=min xi = 2, в = max xi = =10, поэтому (в-а)/5=1.6 и границы интервалов будут ξ0 = 2, ξ1 = 2+1.6=3.6, ξ2 = =3.6+1.6=5.2, ξ3 = 5.2+1.6=6.8, ξ4 = 6.8+1.6= 8.4, ξ5 = 8.4+1.6=10.
Эмпирическая частота rj интервала 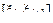 (j =0,..,4) подсчитывается с помощью ряда как число наблюдений, попавших в интервал, отнесённое к объёму выборки n. Так, в первый (j =0) интервал [2;3.6] попало 4+10=14 значений, поэтому r0 = = 14/100 =0.14. Aналогично, r1= 0.21, r2=0.3, r3=0.2, r4=0.15.
(j =0,..,4) подсчитывается с помощью ряда как число наблюдений, попавших в интервал, отнесённое к объёму выборки n. Так, в первый (j =0) интервал [2;3.6] попало 4+10=14 значений, поэтому r0 = = 14/100 =0.14. Aналогично, r1= 0.21, r2=0.3, r3=0.2, r4=0.15.
2. Примем в качестве параметров нормального распределения Х вычисленные в задаче8.1 значения точечных оценок
M[X] =  = 6.23, s[X] = s = 2.06
= 6.23, s[X] = s = 2.06
Теоретические частоты 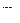 интервалов
интервалов 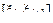 (j =0,1,..,4) являются вероятностями
(j =0,1,..,4) являются вероятностями
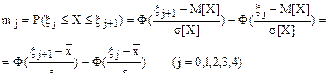
С помощью таблиц интеграла Лапласа находим
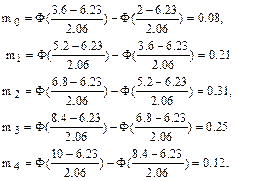
3. Вычисляем значение
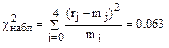
По таблице распределения χ2 Пирсона для доверительной вероятности g = 1-α = 0.9 и числа степеней свободы n = 3 находим значение  . Поскольку
. Поскольку 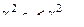 гипотезу о нормальном распределении СВ Х следует считать не противоречащей выборочным данным.
гипотезу о нормальном распределении СВ Х следует считать не противоречащей выборочным данным.
Задание 8.4.
По заданной корреляционной таблице найти выборочные средние 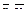 среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние
среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние  по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
| Y X | 0 | 2 | 4 | 6 | 8 | nX |
| 1 | 3 | 3 | ||||
| 3 | 2 | 3 | 5 | 10 | ||
| 5 | 9 | 8 | 17 | |||
| 7 | 2 | 6 | 8 | |||
| 9 | 4 | 1 | 5 | |||
| 11 | 7 | 7 | ||||
| nY | 5 | 12 | 15 | 10 | 8 | 50 |
Решение. Вычислим выборочные средние и среднеквадратические отклонения для X,Y


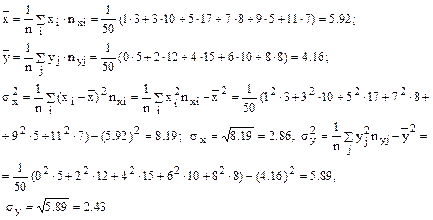
Выборочный коэффициент корреляции между Х и У отыскивается по формуле
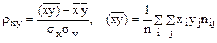
Согласно таблице

откуда
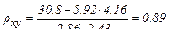
Выборочное линейное уравнение регрессии У на Х имеет вид
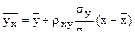
или, с учётом вычисленных значений,
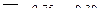 (1)
(1)
Условное среднее при x = xi вычисляется по формуле
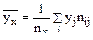
где  - число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим
- число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим
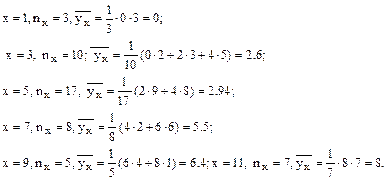 2)
2)
Значения условных средних  , отыскиваемые по уравнению регрессии (1):
, отыскиваемые по уравнению регрессии (1):

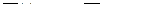

Отклонения значений (2), (3)  будут
будут
d1 = 0-0.45=-0.45; d2 = 2.6- 1.96 = 0.65; d3 = -0.51, d4 = 0.55; d5 = -0.05;
d6 = 0.05.
Наибольшее по абсолютной величине отклонение равно 0.65.
С о д е р ж а н и е
| 1. | Контрольные работы..................................... | ||
| 1.1. | Правила оформления контрольных работ.................... | 3 | |
| 1.2. | Выбор варианта контрольной работы........................ | 3 | |
| 1.3. | Задания контрольных работ................................. | ||
| К о н т р о л ь н а я р а б о т а № 5.............................. | 4 | ||
| К о н т р о л ь н а я р а б о т а № 6.............................. | 18 | ||
| К о н т р о л ь н а я р а б о т а № 7.............................. | 37 | ||
| К о н т р о л ь н а я р а б о т а № 8.............................. | 59 | ||
| 2. | Примеры решения задач контрольных работ....... | ||
| 2.1. | Решение типового варианта контрольной работы № 1......... | 75 | |
| 2.2. | Решение типового варианта контрольной работы № 2......... | 85 | |
| 2.3. | Решение типового варианта контрольной работы № 3......... | 96 | |
| 2.4. | Решение типового варианта контрольной работы № 4......... | 105 | |
Учебное издание
Высшая математика
Программа, методические указания и контрольные задания
для студентов-заочников инженерных и
инженерно-экономических специальностей
приборостроительного факультета
В 2-х частях
Ч а с т ь II
Составители: ИБРАГИМОВ Владислав Ахмедович
СТРЕЛЬЦОВ Сергей Викторович
МЕЛЕШКО Алексей Николаевич
БОКУТЬ Людмила Валентиновна


