 |
Www//isu6/library/index.htm.
|
|
|
|
МЕХАНИКА ЖИДКОСТИ И ГАЗА
Учебно-методическое пособие

УДК 532(075.8)+533(075.8)
ББК 22.365я73
М55
Печатается по решению научно-методического совета географического
факультета Иркутского государственного университета
Рецензенты:
П. Г. Ковадло, д-р физ.-мат. наук, проф. кафедры метеорологии
и охраны атмосферы Иркутского госуниверситета;
Т. В. Ходжер, д-р геогр. наук, зам. директора
Лимнологического ин-та СО РАН

Механика жидкости и газа: учеб.-метод. пособие / сост. В. К. Аргучинцев, А. В. Аргучинцева. – Иркутск: Изд-во Иркут. гос. ун-та, 2010. – 59 с.
Приводится программа по дисциплине «Механика жидкости и газа», в которой ко всем разделам указаны ссылки на основную и дополнительную литературу. В пособии даны основные понятия изучаемой дисциплины и приведены подробные решения типовых задач, что позволяет самостоятельно выполнить прилагаемые контрольные работы. В приложении даны основные необходимые понятия по высшей математике.
Предназначено для студентов очной и заочной форм обучения специальностей 020601 – Гидрология, 020602 – Метеорология, 020802 – Природопользование.
Работа выполнена при частичной финансовой поддержке программ «Фундаментальные исследования и высшее образование» (проект НОЦ-017 «Байкал»), «Развитие научного потенциала высшей школы (2009–2010 гг.)» (проект РНП.2.2.1.1/5901) и Госконтракта
№ 02.740.11.0335 на выполнение научно-исследовательских работ
УДК 532(075.8)+533(075.8)
ББК 22.365я73
© Аргучинцев В. К., Аргучинцева А. К., сост., 2010
© ГОУ ВПО «Иркутский государственный
университет», 2010
СОДЕРЖАНИЕ
Программа курса............................................................ 4
Рекомендуемая литература......................................... 8
|
|
|
Список учебников и пособий в электронном виде.... 9
Введение......................................................................... 10
Кинематика..................................................................... 14
Динамика......................................................................... 29
Решение типовых задач................................................ 41
Контрольная работа для студентов III курса з/о
специальностей «Гидрология» и
«Природопользование»................................................. 45
Контрольная работа для студентов III курса з/о
специальности «Метеорология».................................. 47
Основные понятия математики.................................... 48
ПРОГРАММА КУРСА
| Тема занятий | Рекомендуемая литература |
| Введение Теоретическая механика и ее основные разделы. Основные положения, изучаемые в каждом разделе. Место в ряду естественных наук. Главные задачи, решаемые в каждом разделе механики, области их применения. Механика жидкости и газа – один из разделов теоретической механики. Механика жидкости и газа и ее основные разделы: кинематика, статика, динамика. Механика жидкости и газа – научный фундамент метеорологии, гидрологии, природопользования. Достижения мировой науки и роль отечественных ученых. | [1], п. 1,2; [6], гл. 2; [5], гл. 2; [10], л. 1. |
| Кинематика Понятие о сплошной среде. Кинематика материальной точки и абсолютно твердого тела. Жидкая частица (элементарный объем). Плотность. Общность и различия между капельной жидкостью и газом. Жидкости сжимаемые и несжимаемые. Градиент скалярной величины. Два основных метода описания движения жидкости – Лагранжа и Эйлера. Индивидуальная (субстанциональная) производная, ее разложение на локальную и конвективную составляющие. | [1], п. 16, 18; [3], гл. 1; [5], гл. 2; [9], гл. 2, п. 1, 2; [10], л. 1, 2; [11], гл. 1. |
| Траектории и линии тока, их дифференциальные уравнения. Установившееся движение. Трубка тока. Струя. | [1], п. 11; [5], гл. 2; [10], л. 1, 4; [11], гл. 1; [12], п. 1.3. |
| Поток векторного поля через поверхность. Дивергенция. Формула Остроградского – Гаусса в векторном виде. | [10], л. 4; [11], гл. 1; [12], п. 1.4, 1.5. |
| Вывод уравнения неразрывности. Частные виды уравнения неразрывности. Гидравлическое уравнение неразрывности. | [1], п. 18; [2], п. 1; [3], гл. 1, 2; [7], гл. 1, 2; [10], л. 7, 8; [11], гл. 1; [12], п. 2.3. |
| Циркуляция вектора скорости по замкнутому контуру. Вихрь скорости. Теорема Стокса в векторной форме. Связь между ротором вектора скорости и угловой скоростью вращения твердого тела. | [1], п. 10; [10], л. 5; [11], гл. 1; [12], п. 1.6, 1.7. |
| Теорема Коши – Гельмгольца (I-я теорема Гельмгольца) о движении жидкой частицы. Скорость деформации. Физический смысл составляющих тензора деформаций: деформации растяжения, сжатия, сдвига. | [1], п. 12, 13; [3], гл. 1; [4], гл. 2, п. 2; [10], л. 14, 15; [11], гл. 1; [12], п. 1.11. |
| Вихревое движение жидкости. Вихревая линия и ее дифференциальное уравнение. Вихревая трубка. 2-я теорема Гельмгольца (о постоянстве потока вихря скорости через произвольное сечение вихревой трубки). Интенсивность вихревой трубки. Теорема Стокса о связи интенсивности вихревой трубки с циркуляцией по замкнутому контуру, охватывающему трубку. | [1], п. 14, 15; [3], гл. 1, п. 19; [10], л. 5; [11], гл. 1. |
| Безвихревое движение. Потенциал скорости. Уравнение неразрывности для потенциального движения. | [1], п. 46, 47, 49; [2], п. 9; [3], гл. 1. |
| Плоско-параллельное движение несжимаемой жидкости. Функция тока. Безвихревое плоскопараллельное движение. Связь потенциала скорости с функцией тока и геометрическая интерпретация этой связи. | [1], п. 49; [3], гл. 4. |
| Потенциалы скоростей и функций тока простейших потоков. | [3], гл. 1, п. 16; гл. 4, п. 13. |
| ДИНАМИКА Динамика идеальной жидкости. Классификация сил, действующих в жидкости: массовые, поверхностные силы. Примеры сил. | [1], п. 19; [3], гл. 2, п. 1; [11], гл. 1; [12], п. 2.1. |
| Модели жидкости. Независимость гидродинамического давления в идеальной жидкости от направления. Векторное уравнение движения идеальной жидкости. Уравнения движения идеальной жидкости в форме Эйлера. Уравнения движения жидкости в форме Громека. Общая постановка задач гидродинамики. Случай несжимаемой жидкости. Случай сжимаемой жидкости. Баротропность и бароклинность. Уравнение притока энергии. Начальные и граничные условия (на свободной поверхности и на твердой стенке). | [1], п. 29; [2], п. 2; [3], гл. 2; [10], л. 7. [3], гл. 2; [12], п. 5.1, 5.2. |
| Интегралы уравнений движения идеальной жидкости (Бернулли, Лагранжа, Лагранжа – Бернулли). Их физическая и геометрическая интерпретации. | [1], п. 48; [2], п. 5; [10], л. 8. |
| Динамические свойства вихревого движения (основные уравнения теории вихрей, примеры образования вихрей). | [3], гл. 5. |
| Уравнения гидростатики. Условия для сил, удерживающих жидкость в равновесии. Закон Паскаля. Равновесие тяжелой жидкости. | [1], п. 26; [2], п. 3; [3], гл. 3; [10], гл. 8, п. 1. |
| Волновые движения идеальной жидкости: различные типы волн; основные уравнения теории волн. | [3], гл. 8. |
| Уравнения движения вязкой жидкости в напряжениях (в форме Навье). Гипотезы Стокса. Уравнения движения вязкой жидкости в форме Навье – Стокса. Закон Ньютона. Коэффициент вязкости. | [1], п. 20, 21, 86; [2], п. 15; [7], гл. 8.1; [10], л. 10; [12]. |
| Уравнение притока тепла для вязкой сжимаемой жидкости. Диссипация механической энергии. | [2], п. 49; [4], гл. 2, п. 10; [10], л. 11; [11], гл. 2. |
| Понятие подобия. Необходимые и достаточные условия подобия. Обезразмеривание уравнений. Критерии подобия. Физический смысл критериев подобия. | [1], п. 87, 88; [2], п. 19; [4], гл. 2, п. 9; [7], гл. 3.3; [10], л. 13; [11], гл. 2; [12], п. 2.9. |
| Интегрирование уравнений динамики вязкой жидкости. Движение при больших значениях числа Рейнольдса. Ламинарный пограничный слой. Основные уравнения ламинарного пограничного слоя. Интегральные соотношения пограничного слоя. Переход от ламинарного движения к турбулентному. Критическое число Рейнольдса. Методы осреднения. Уравнения Рейнольдса осредненного турбулентного движения. Путь смешения. Изотропная и однородная турбулентность. Проблема замыкания. Турбулентные течения в термически стратифицированных средах. | [1], п. 120, 121, 122; [2], п. 20, 21, 26; [7], гл. 9.1; [12], п. 2.6. |
|
|
|
|
|
|
Принятые сокращения: гл. – глава, п. – параграф, л. – лекция.
Весь излагаемый материал и значительное его расширение можно найти по внутреннему электронному адресу в компьютерных классах географического факультета:
|
|
|
www//isu6/library/index.htm.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная
1. Лойцянский Л. Г. Механика жидкости и газа / Л. Г. Лойцянский. – М.: Дрофа, 2003. – 840 с.
2. Ландау Л. Д. Гидродинамика (Теоретическая физика,
т. VI) / Л. Д. Ландау, Е. М. Лифшиц. – М.: Наука, 1986. – 736 с.
3. Кочин Н. Е. Теоретическая гидромеханика. I, II / Н. Е. Кочин, И. А. Кибель, Н. В. Розе. – М.: Изд-во физ.-мат. лит-ры, 1963. – Ч. I. – 584 с.; Ч. II. – 727 с.
4. Золотов С. С. Задачник по гидромеханике / С. С. Золотов,
В. Б. Амфилохиев, Ю. И. Фаддеев. – Л.: Судостроение, 1984. – 230 с.
5. Шашин В. М. Гидромеханика / В. М. Шашин. – М.: Высш. шк., 1990. – 384 с.
Дополнительная
6. Самойлович Г. С. Гидрогазодинамика / Г. С. Самойлович. – М.: Машиностроение, 1990. – 379 с.
7. Бернар Ле Меоте. Введение в гидродинамику и теорию волн на воде / Ле Меоте Бернар. – Л.: Гидрометеоиздат, 1974. – 367 с.
8. Седов Л. И. Механика сплошной среды / Л. И. Седов. –
М.: Наука, 1983 (Т. I), 1984 Т. II). – 528 с. (Т. I), 560 с. (Т. II).
9. Палагин Э. Г. Основы гидромеханики / Э. Г. Палагин,
И. А. Славин. – Л., 1974. – 244 с.
10. Дмитревский В. И. Гидромеханика / В. И. Дмитревский. – М.: Морской транспорт, 1962. – 296 с.
11. Аргучинцев В. К. Общие принципы динамики атмосферы / В. К. Аргучинцев. – Иркутск: РИО ИГУ, 1996. – 133 с.
12. Аргучинцев В. К. Динамическая метеорология атмосферы /
В. К. Аргучинцев. – Иркутск: Изд-во ИГУ, 2009. – 161 с.
СПИСОК УЧЕБНИКОВ И УЧЕБНЫХ ПОСОБИЙ
В ЭЛЕКТРОННОМ ВИДЕ
Биркгоф Г. Гидродинамика / Г. Биркгоф. – М.: Изд-во ин. лит-ры, 1963 (пер. с англ.). – 244 с.
Бэтчелор Дж. Введение в динамику жидкости / Дж. Бэтчелор. – М.: Мир, 1973 (пер. с англ.). – 759 с.
Валландер С. В. Лекции по гидроаэромеханике / С. В. Валландер. – Л.: Ленингр. ун-т, 1978. – 295 с.
Ван-Дайк М. Альбом течений жидкости и газа / М. Ван-Дайк. – М.: Мир, 1986. – 181 с.
Вилля Г. Теория вихрей / Г. Вилля. – Л.; М.: ОНТИ, Гл. ред. общетехн. лит-ры, 1936. – 256 с.
Гельмгольц Г. Основы вихревой теории / Г. Гельмгольц. – М.; Ижевск, Ин-т компьютерных иссл-й, 2002 (пер. с нем.). – 81 с.
Жуковский Н. Е. Собр. соч. Т. II. Гидродинамика / Н. Е. Жуковский. – М.; Л.: Гос. изд-во техн.-теорет. лит-ры, 1949. – 765 с.
Карман Т. Аэродинамика. Избранные темы в их историческом развитии / Т. Карман. – М.: РХД (пер. с англ.), 2002. – 208 с.
Кирхгоф Г. Механика / Г. Кирхгоф. – М.: АН СССР, 1962 (пер. с нем.).– 404 с.
Кочин Н. Е. Теоретическая гидромеханика / Н. Е. Кочин,
И. А. Кибель, Н. В. Розе. – М.: Изд-во физ.-мат. лит-ры, 1963. – Ч. I. – 584 с.; Ч. II. – 727 с.
Лаврентьев М. А. Проблемы гидродинамики и их математические модели / М. А. Лаврентьев, Б. В. Шабат. – М.: Наука, 1973. – 416 с.
Ламб Г. Гидродинамика: пер. с англ. / Г. Ламб. – М.; Л.: ОРГИЗ, 1947. – 929 с.
|
|
|
Ландау Л. Д. Гидродинамика. Т. 6: Теоретическая физика /
Л. Д. Ландау, Е. М. Лифшиц. – М.: Наука, 1986. – 736 с.
Прандтль Л. Гидроаэромеханика: пер. с нем. / Л. Прандтль. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. – 576 с.
Пуанкаре А. Теория вихрей: пер. с фр. / А. Пуанкаре. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. – 160 с.
Рауз Х. Механика жидкости: пер. с англ. / Х. Рауз. – М.: Изд-во лит-ры по строительству, 1967. – 392 с.
ВВЕДЕНИЕ
Для понимания процессов, происходящих в атмосфере и гидросфере, умения правильно их описывать и предсказывать, необходимо изучить разделы теоретической механики, в частности, механику жидкости и газа (с ее составляющими – кинематика, динамика). Изучение материала базируется на знании основ высшей математики, в частности, дифференциального и интегрального исчислений, теории рядов, дифференциальных уравнений, разделов уравнений математической физики и физики твердого тела.
Дисциплина «Механика жидкости и газа» является фундаментальной для изучения других курсов (Динамическая метеорология, Геофизическая гидродинамика, Теория общей циркуляции атмосферы, Теория климата, Численные методы анализа и прогноза погоды, Динамика русловых процессов, Гидравлика, Динамика русловых процессов, Моделирование гидрологических процессов, Моделирование в задачах охраны окружающей среды).
Механика жидкости и газа (гидромеханика) – раздел теоретической механики, в котором изучаются законы движения жидкостей и газов и их взаимодействие с граничащими с ними твердыми телами. Классическая гидромеханика базируется на утверждениях о справедливости классической механики, т. е. механики Ньютона и классической термодинамики. Первое утверждение предполагает, что изучаются движения со скоростями, малыми по сравнению со скоростями света, и рассматриваются макроскопические объекты, размеры которых существенно превосходят размеры микромира. Второе утверждение предполагает, что в окрестности каждой точки жидкость находится в состоянии термодинамического равновесия или близком к нему, вследствие чего можно использовать термодинамические законы.
В настоящее время механика жидкости и газа – широко разветвленная теоретико-экспериментальная наука, способная решать различные прикладные задачи, как например: воздействие жидкости на движущиеся в ней тела (корабли, самолеты, ракеты, снаряды); движение жидкости по трубам и внутри различных машин (проектирование нефте- и газопроводов, насосов, турбин); фильтрация, т.е. движение жидкости через пористые среды (учитывается при строительстве тоннелей, плотин, опор мостов); проблема волновых движений (корабельные волны, теория приливов, распространение волн в каналах); теория турбулентных движений жидкости; возможности описания движения сильно сжатых жидкостей; проблемы кавитации (появление пузырьков, наполненных парами жидкости); условия равновесия жидкостей и тел, плавающих внутри и на поверхности жидкости.
Как и в любой науке, в механике жидкости и газа вводятся некоторые положения, на основе которых строится все здание науки. Такими основными положениями в механике жидкости и газа являются: гипотеза сплошности, понятие жидкого элементарного объема, плотность жидкости, сжимаемость и несжимаемость жидкости. Рассмотрим эти понятия подробнее.
Гипотеза сплошности. В механике жидкости и газа, как и в механике твердого тела, отвлекаются от молекулярного строения вещества, рассматривая жидкость (газ) как сплошную среду, в которой отсутствуют межмолекулярные пустоты и молекулярное движение. Иначе говоря, предполагают замену реальной жидкости с ее дискретным молекулярным строением моделью сплошного распределения вещества по рассматриваемому объему. Это предположение называется гипотезой сплошности или непрерывности среды. Гипотеза сплошности позволяет рассматривать все кинематические и динамические характеристики среды как непрерывные функции своих аргументов (например, пространственных декартовых координат x,y,z и времени t), что дает возможность использовать математический аппарат, разработанный для непрерывных функций.
Под жидким элементарным объемом (или элементарным объемом) понимают объем, линейные размеры которого, с одной стороны, ничтожно малы по сравнению с размерами изучаемого объекта (например, озером, рекой, каналом, воздушным пространством над изучаемым объектом и пр.), но, с другой стороны, достаточно велики по сравнению с объемом отдельной молекулы (или длиной свободного пробега молекул). Жидкий элементарный объем вмещает в себя настолько большое число молекул, что к ним может быть применено статистическое осреднение, связанное с понятием сплошности среды.
Плотность характеризует распределение массы в объеме. Выделим в жидкости достаточно малый объем 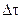 сплошной среды, массу жидкости в котором обозначим
сплошной среды, массу жидкости в котором обозначим  . Тогда
. Тогда
 – средняя плотность сплошной среды в объеме
– средняя плотность сплошной среды в объеме 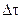 .
.
При стягивании объема в точку получим предельное значение плотности
 (1)
(1)
называемое плотностью распределения среды в данной точке. В общем случае плотность – функция пространственных координат и времени:
 .
.
В системе единиц СИ размерность плотности  , т. е.
, т. е.  .
.
Жидкости и газы, обладая общими свойствами (непрерывностью, легкой подвижностью или текучестью), отличаются друг от друга по своим физическим свойствам, что обусловлено различием их внутренней молекулярной структуры.
В жидкостях межмолекулярные расстояния очень малы по сравнению с газами, что приводит к возникновению значительных молекулярных сил сцепления, которые препятствуют изменению объема. Такие жидкости называются несжимаемыми (или капельными). Несжимаемая жидкость может изменять только свою форму (но не объем). Например, принесенный из магазина один литр молока не изменит свой объем, куда бы это молоко Вы не перелили, масса молока то же остается неизменной, а потому плотность молока не изменяется. Расходуя молоко, Вы меняете его объем пропорционально массе, а потому опять плотность остается постоянной. Капельные жидкости в поле силы тяжести могут иметь граничную поверхность (например, вода).
В газах межмолекулярные расстояния (по сравнению с капельными жидкостями) велики, а, следовательно, молекулярные силы сцепления малы. Поэтому газы легко могут менять свой объем, и их называют сжимаемыми жидкостями. Сжимаемые жидкости могут изменять как свою форму, так и объем. Например, в баллончике находится сжатый газ. Этот газ из баллончика можно выпустить, и он заполнит все представляемое им пространство (комнату). Объем газа изменится (увеличится), а масса останется постоянной. Согласно формуле (1), плотность газа уменьшится. Газообразные жидкости заполняют весь сосуд, в который они помещены.
Однако, с точки зрения общности, жидкости и газы называют одним термином – жидкость, различая, когда это необходимо, на несжимаемые и сжимаемые жидкости. В сжимаемой жидкости может иметь место изменение как ее формы, так и объема.
КИНЕМАТИКА
Кинема́тика (греч. κινειν — двигаться) в физике – раздел механики, изучающий движение идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость) с геометрической точки зрения без выяснения причин движения (массы, сил и т. д.). Исходные понятия кинематики – пространство и время. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел в пространстве и во времени. Фундамент классической кинематики заложил итальянский ученый Галилео Галилей (1564–1642).
В кинематике рассматривают два основных метода описания движения жидкости: метод Лагранжа (1736–1813) и метод Эйлера (1707–1783).
По методу Лагранжа следят за движением отдельной жидкой частицы. В некоторый (начальный) момент времени t0 каждая из жидких частиц маркируется путем присвоения ей значений координат в данный момент времени: х0 = а, у0 = b, z0 = c. В дальнейшем прослеживается движение каждой жидкой частицы индивидуально. Движение жидкой частицы будет выясненным, если в каждый момент времени t > t0 известно ее местонахождение (координаты х,у,z):
 ;
;
 ;
;
 .
.
Начальные координаты a,b,c выделенной частицы в момент времени t0 называют переменными Лагранжа.
Составляющие проекций скорости 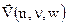 рассматриваемой частицы на координатные оси декартовой прямоугольной системы координат имеют вид:
рассматриваемой частицы на координатные оси декартовой прямоугольной системы координат имеют вид:
 ,
,  ,
,  . (2)
. (2)
Аналогично, составляющие ускорения  на соответствующие координатные оси запишутся в виде:
на соответствующие координатные оси запишутся в виде:
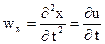 ,
,  ,
,  . (3)
. (3)
В формулах (2) и (3) при дифференцировании параметры a,b,c являются постоянными, следовательно, x,y,z и  зависят только от времени.
зависят только от времени.
Методом Лагранжа, например, определяют в интересуемый момент времени координаты запускаемых аппаратов (метеорологические радиозонды, спутники и пр.).
По методу Эйлера следят в неподвижной точке пространства (гидрологический пост, метеостанция) за изменением характеристик движущегося потока жидкости в этой точке. Частицы жидкости, проходящие через точку (x,y,z) в последовательные моменты времени, будут обладать определенными скоростями  . Поэтому в данной точке скорость
. Поэтому в данной точке скорость  есть функция времени
есть функция времени  . Но скорость
. Но скорость  неодинакова для различных точек пространства, а потому в общем случае она должна быть функцией четырех переменных
неодинакова для различных точек пространства, а потому в общем случае она должна быть функцией четырех переменных
 . (4)
. (4)
Переменные x,y,z,t называют переменными Эйлера. Дифференцируя (4), получим ускорение
 .
.
Используя обозначения 

 имеем:
имеем:
 (5)
(5)
Проектируя (5) последовательно на координатные оси, получим формулы для компонентов ускорения жидкой частицы:
 (6)
(6)
Все члены в (5) и (6) имеют специальные названия:
 
| – индивидуальная (субстанциональная, полная) производная с указанными в скобках компонентами – проекциями вектора скорости на соответствующие координатные оси; |

| – локальная (местная, или частная) производная, характеризующая изменение рассматриваемой величины с течением времени в данной точке пространства; |

| – конвективная производная, |
которой соответствуют скалярные записи в равенствах (6):

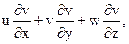
 .
.
Конвективная производная появляется вследствие перемещения частицы жидкости в неоднородном поле рассматриваемой величины, причем, в свою очередь, она распадается на адвекцию (перенос по горизонтали – производные по х и y) и конвекцию (перенос по вертикали – производная по z).
Уравнения (5)–(6) можно записать в виде:
 (7)
(7)
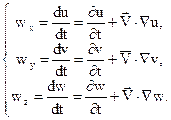 (8)
(8)
Здесь  – оператор градиента, действующий на соответствующую функцию
– оператор градиента, действующий на соответствующую функцию  .
.
Из последних записей (7)–(8) видно, что конвективная производная может возникнуть только в неоднородном движущемся поле.
Движение жидкости будет стационарным (установившимся), если скорости частиц жидкости явным образом не зависят от времени, т. е.  или, что то же,
или, что то же,  . В противном случае – движение нестационарное (неустановившееся).
. В противном случае – движение нестационарное (неустановившееся).
Двум описаниям движения жидкости соответствуют и две ее геометрические характеристики: траектория и линия тока.
Траектория – линия, по которой движется жидкая частица в течение некоторого отрезка времени (пространственный след, оставляемый жидкой частицей). В переменных Лагранжа траекторию можно определить, используя соотношения (2), благодаря которым можно записать:
 . (9)
. (9)
Система уравнений (9) – это дифференциальные уравнения траектории движения частицы.
Интегрируя (9) и разрешая относительно x, y, z, получим:


 ,
,
где С1, С2, С3 – константы интегрирования, значения которых можно определить из заданных начальных условий. Исключая из последней системы уравнений время t, найдем траекторию жидкой частицы.
Линия тока – линия, проведенная в жидкости в данный момент времени так, что скорости всех частиц, находящихся на этой линии, направлены по касательным к этой линии.
Дифференциальные уравнения линии тока:
 . (10)
. (10)
Время t в (10) – фиксированный параметр.
Таким образом, линии тока характеризуют картину движения в данный момент времени, а траектории – пространственный след движущейся частицы во времени.
Через каждую точку поля скоростей, в которой функции  не обращаются в нуль, в данный момент времени проходит только одна линия тока. Исключение составляют точки, через которые проходит несколько и даже бесчисленное количество линий тока. Эти точки называются особенными.
не обращаются в нуль, в данный момент времени проходит только одна линия тока. Исключение составляют точки, через которые проходит несколько и даже бесчисленное количество линий тока. Эти точки называются особенными.
В качестве примера особых точек, где скорость равна нулю, можно указать на разветвления потока, охватывающего тело в его начале и конце. Эти точки называют критическими (рис. 1).
Другим примером особой точки является так называемый точечный источник (рис. 2, а) или точечный сток (рис. 2, б).

Рис. 1. Обтекание тела
Источником называется точка, из которой в каждый момент времени непрерывно и равномерно выделяется жидкость и растекается по радиусам во все стороны (см. рис. 2, а). Стоком называется точка, в которой жидкость в каждый момент времени непрерывно и равномерно поглощается одинаково по всем направлениям (см. рис. 2, б). Стрелки на линиях показывают направление течения жидкости.
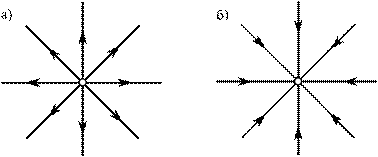
Рис. 2. Источник (а), сток (б)
Совокупность линий тока образуют поверхность тока, а часть жидкости, выделенная из нее поверхностью тока, проведенной через замкнутый контур, называется трубкой тока (рис. 3) с сечением  .
.
Часть жидкости, ограниченная траекториями точек замкнутого контура, называется струей.

Рис. 3. Трубка тока с сечением S
Для стационарного движения линии тока совпадают с траекториями, а следовательно и трубки тока совпадают со струей. В нестационарных течениях траектории отличаются от линий тока, трубки тока – от струи.
Поток векторного поля через поверхность. Предположим, что в некоторой части пространства задано течение несжимаемой жидкости с постоянной скоростью  . Перпендикулярно скорости движения поставлена проницаемая пластинка площадью
. Перпендикулярно скорости движения поставлена проницаемая пластинка площадью  (рис. 4). Объем жидкости
(рис. 4). Объем жидкости  , протекающий через данную пластинку за единицу времени, очевидно, будет
, протекающий через данную пластинку за единицу времени, очевидно, будет
P = VS, (11)
так как все частицы жидкости, находящиеся в начальный момент перед пластинкой на расстоянии не более чем  , за единицу времени пройдут через пластинку (вспомните, расстояние равно произведению скорости на время). Величину этого объема
, за единицу времени пройдут через пластинку (вспомните, расстояние равно произведению скорости на время). Величину этого объема  называют потоком постоянного вектора
называют потоком постоянного вектора  через площадку
через площадку  .
.
Пусть теперь пластинка поставлена к потоку под некоторым углом  (рис. 5), где угол
(рис. 5), где угол  – угол между вектором скорости
– угол между вектором скорости  и перпендикуляром
и перпендикуляром  к площадке
к площадке  , направленным в сторону общего потока жидкости.
, направленным в сторону общего потока жидкости.
В этом случае через пластинку  пройдут за единицу времени те частицы, которые отстояли от этой пластинки на расстоянии не более
пройдут за единицу времени те частицы, которые отстояли от этой пластинки на расстоянии не более  , т. е.
, т. е.
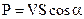 . (12)
. (12)


Рис. 4. Поток вектора скорости Рис. 5. Поток вектора скорости
к перпендикулярной площадке S под углом α к площадке S
Очевидно, что (11) – частный случай (12), так как при 
 ,
,  (
(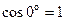 ).
).
Равенство (12) можно записать в векторном виде:
 ,
,
где  – проекция вектора
– проекция вектора  на направление единичного вектора
на направление единичного вектора  .
.
Теперь можно определить поток произвольного вектора  через поверхность
через поверхность  (замкнутую или незамкнутую) (рис. 6). В каждой точке поверхности построим единичный вектор нормали
(замкнутую или незамкнутую) (рис. 6). В каждой точке поверхности построим единичный вектор нормали  и условимся для замкнутой поверхности считать за положительное направление нормали – направление внешней нормали. Если поверхность
и условимся для замкнутой поверхности считать за положительное направление нормали – направление внешней нормали. Если поверхность  незамкнута, то направление нормали произвольно (оговаривая какое из направлений мы выбираем), при этом векторы
незамкнута, то направление нормали произвольно (оговаривая какое из направлений мы выбираем), при этом векторы  во всех точках поверхности должны лежать по одну ее сторону.
во всех точках поверхности должны лежать по одну ее сторону.
Разобьем поверхность  (см. рис. 6) на большое число элементарных площадок, в каждой из которых выберем произвольно точку
(см. рис. 6) на большое число элементарных площадок, в каждой из которых выберем произвольно точку  и построим в ней
и построим в ней  . Составим интегральную сумму
. Составим интегральную сумму
 ,
,
где  – число элементарных площадок разбиения,
– число элементарных площадок разбиения,  – угол между
– угол между  и
и  .
.

Рис. 6. Поток произвольного вектора  через поверхность
через поверхность
Потоком Р поля вектора  через поверхность
через поверхность  называется предел интегральной суммы
называется предел интегральной суммы  при стягивании каждой элементарной площадки в точку
при стягивании каждой элементарной площадки в точку
 . (13)
. (13)
Физический смысл потока векторного поля в случае гидродинамической интерпретации при
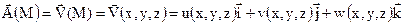
представляет поток вектора скорости через поверхность, т. е. объем жидкости  , протекающий за единицу времени через эту поверхность:
, протекающий за единицу времени через эту поверхность:
 .
.
Если поверхность замкнута, то ориентируя поверхность по внешней нормали (рис. 7), будем иметь:
а)  , если жидкость вытекает, так как
, если жидкость вытекает, так как  ,
, 
б)  , если жидкость втекает, так как
, если жидкость втекает, так как  .
.
В целом  . Причем, если
. Причем, если  , то говорят, что жидкости вытекает больше, чем втекает, т. е. внутри замкнутого объема имеются источники (например, тает лед). Если
, то говорят, что жидкости вытекает больше, чем втекает, т. е. внутри замкнутого объема имеются источники (например, тает лед). Если  , то жидкости втекает больше, чем вытекает, т. е. внутри замкнутого объема имеются стоки (например, жидкость испаряется). Если
, то жидкости втекает больше, чем вытекает, т. е. внутри замкнутого объема имеются стоки (например, жидкость испаряется). Если  , то в жидкости либо нет источников и стоков, либо они компенсируют друг друга. Надо отметить, что и в первых двух случаях в замкнутом объеме могут быть и источники, и стоки, но в первом случае источники превалируют над стоками, а во втором – стоки превалируют над источниками.
, то в жидкости либо нет источников и стоков, либо они компенсируют друг друга. Надо отметить, что и в первых двух случаях в замкнутом объеме могут быть и источники, и стоки, но в первом случае источники превалируют над стоками, а во втором – стоки превалируют над источниками.

Рис. 7. Втекание и вытекание жидкости через замкнутую поверхность
Дивергенция (расходимость) векторного поля характеризует отсутствие или наличие в точке поля источника или стока:
 ,
,
где  – поток произвольного векторного поля
– поток произвольного векторного поля  через замкнутую поверхность S (элементарная замкнутая поверхность
через замкнутую поверхность S (элементарная замкнутая поверхность  , где
, где  – ориентация площадки внешней нормалью), ограничивающей объем
– ориентация площадки внешней нормалью), ограничивающей объем  . Если
. Если  > 0, то в рассматриваемой точке имеется источник; если
> 0, то в рассматриваемой точке имеется источник; если  < 0, то – сток; если
< 0, то – сток; если  = 0, то в данной точке нет ни источника, ни стока.
= 0, то в данной точке нет ни источника, ни стока.
Дивергенция векторного поля  в точке рассчитывается по формуле:
в точке рассчитывается по формуле:
 .
.
Если векторное поле скоростное, то есть  , то
, то 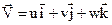 , и
, и
 . (14)
. (14)
Уравнение неразрывности (сплошности). Очевидно, что поток скорости выражает объем жидкости, протекающий за единицу времени через поверхность S, которая считается неподвижной. При замкнутой поверхности вытекающий из нее объем считается положительным (по направлению совпадает с ориентацией внешней нормали), а втекающий – отрицательным (направление противоположно ориентации внешней нормали). Рассматривая в пространстве протекание жидкости через замкнутую поверхность, можно заключить, что если за некоторый промежуток времени количество вытекающей жидкости не будет равно количеству втекающей, то внутри объем этой жидкости произойдет изменение плотности. Аналитически этот факт описывается уравнением неразрывности:
 , (15)
, (15)
которое является выражением закона сохранения масс (материи), установленны
|
|
|


