Частные производные, частные дифференциалы, полный дифференциал

Рассматриваются для функций более одной независимой переменной. Например, функция . Точка с координатами может смещаться не только на любое расстояние, но и в любом направлении. Скорость изменения функции будет различной при смещении этой точки в различных направлениях. Частные производные по переменным имеют вид:

,

,

.

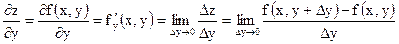Аналогичные записи для функций трех, четырех и т.д. независимых переменных.

Частный дифференциал: , .

Полный дифференциал: .

Для отыскания частных производных остаются справедливыми формулы и правила дифференцирования функции одной переменной.

Если в функции переменная , т. е. , то есть сложная функция и ее частные производные имеют вид:

, .

Теорема о среднем (теорема Лагранжа):

Если функция дифференцируема в замкнутом промежутке , то отношение равно производной, вычисленной в некоторой внутренней точке промежутка

.

Неопределенный интеграл

Задача нахождения первоначального вида функции (первообразной) по известной ее производной называется интегрированием. Так как при дифференцировании любой постоянной мы получаем нуль, то восстановить первообразную мы можем только с точностью до произвольного слагаемого (С). Под буквой С подразумевается любое (как положительное, так и отрицательное постоянное число). Итак, совокупность всех первообразных функций, имеющих одну и ту же производную (дифференциал), называют неопределенным интегралом:

 

,

 

где – подынтегральная функция, – подынтегральное выражение.

Неопределенный интеграл геометрически представляет бесконечное множество (семейство) кривых, отличающихся друг от друга на константу. Чтобы выделить из этого семейства вполне определенную кривую, надо задать какое-нибудь дополнительное условие, которое позволит определить константу С.

Таблица основных формул интегрирования

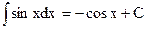
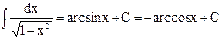
Формула интегрирования по частям:

Определенный интеграл. Принципиальное отличие неопределенного интеграла от определенного: неопределенный интеграл – это функция, производная которой равна подынтегральной функции; определенный интеграл, поскольку он является пределом интегральной суммы, есть некоторое определенное число. Геометрически определенный интеграл представляет площадь криволинейной трапеции, ограниченной графиком функции, осью абсцисс и двумя ординатами концов отрезка (пределами интегрирования), на котором рассматривается интеграл.

Формула Лейбница – Ньютона:

.

Двойной интеграл по поверхности

.

В подавляющем большинстве случаев вычисление двойного интеграла сводится к двум последовательным интегрированиям:

.

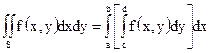Тройной интеграл по объему

.

Как и в случае двойных интегралов, основной прием, на котором базируется вычисление тройных интегралов, состоит в сведении тройного интеграла к повторному интегрированию, т. е. замене интегрирования по объему интегрированием по каждой из переменных в отдельности:

.

Криволинейный интеграл по координатам на плоскости легче представить на конкретной физической задаче.Пусть в плоскости задана какая-то кривая АВ, в каждой точке М которой задана сила . Компоненты силы на оси координат обозначим 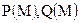. Определим работу по перемещению точки вдоль некоторой линии АВ. Если сила постоянна, а путь АВ прямолинеен, то работа равна, как известно из физики, произведению величины этой силы на длину пути и косинус угла между вектором силы и направлением перемещения, т. е. работа равна скалярному произведению .

В общем случае, когда сила переменна, а путь криволинеен, то необходимо эту кривую АВ разбить на части точками . Соединив полученные точки отрезками прямых, получим ломаную линию. Считая, что вдоль каждого звена ломаной линии работа постоянна, а путь прямолинеен, можем найти работу по перемещению вдоль всей ломаной:

, где – количество точек разбиения линии .

Эту сумму можно принять за приближенное значение работы в силовом поле. Для получения точного значения этой работы надо перейти в последней сумме к пределу, устремив максимальную длину отрезка ломаной линии к нулю. Если при этом сумма стремится к некоторому конечному пределу, то его называют криволинейным интегралом вектора по контуру АВ:

Если контур замкнут, то криволинейный интеграл по замкнутому контуру записывают

.

В этом случае криволинейный интеграл называют циркуляцией (круговое движение) вектора по замкнутому контуру . Если циркуляция положительна, то контур будет вращаться в положительном направлении (против направления обхода часовой стрелки), если циркуляция отрицательна – в отрицательном направлении (по часовой стрелке). Если величина циркуляции равна нулю, то контур вращаться не будет. Итак, циркуляция по данному контуру характеризует вращательное движение поля на данном контуре.

Связь между поверхностным, тройным и криволинейным интегралами:

– формула Остроградского – Гаусса, где – суть углы, составленные внешней нормалью к поверхности с координатными осями.

– формула Стокса.

Ряд Тейлора – разложение функции в окрестности точки :

Ряд Маклорена – разложение функции в окрестности точки :

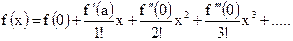
Теорема Лапласа. Если элементы некоторого столбца (строки) определителя умножить на соответствующие им алгебраические дополнения А_ij и эти произведения сложить, то получим значение данного определителя. Иначе, любой определитель можно разложить по элементам какой-либо строки или какого-либо столбца. Например, дан определитель третьего порядка; – его элементы, – номер строки, – номер столбца; минор – это определитель, полученный из данного путем вычеркивания строки и столбца; , т. е. минор, взятый со знаком плюс или минус в зависимости от четности или нечетности суммы 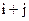. Приведем разложение по первой строке:

Скаляром называют величину, характеризующуюся при выбранной единице меры одним числом. Примерами скалярных величин являются отвлеченное число, температура, плотность среды, энергия и т. п. Два скаляра равны, если при измерении их одной и той же единицей меры получаются одинаковые числа.

Вектором называется величина, характеризующаяся численным значением и направлением в пространстве. Численное значение вектора называется величиной, модулем, нормой или длиной вектора. Это – величина скалярная. Например, вектор 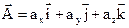имеет проекции на координатные оси соответственно ; – единичные векторы (орты) длиной 1 в выбранном масштабе и направлены по осям соответственно . Модуль вектора равен корню квадратному из суммы квадратов его проекций: . Заметим, так как речь идет о длине вектора, то в рассмотрение принимается только арифметический корень.

Скалярным или векторным полем называется часть пространства, каждой точке которого отнесено соответственно значение некоторой скалярной или векторной величины.

123	Поделиться:

Воспользуйтесь поиском по сайту: