 |
Для студентов III курса з/о специальностей
|
|
|
|
«Гидрология» и «Природопользование»
Задание 1. Определить семейство линий тока, а также линию тока, проходящую через точку А(1,1) в момент времени
t = 0. Определить траекторию частицы, которая в момент времени t = 0 находилась в точке А. Задано поле скоростей: u =2x; v = 3t;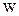 
= 0.
Задание 2. Компоненты поля скорости имеют вид:
, 
, 
.
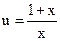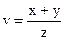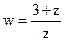1. Определить, будет ли:
а) жидкость несжимаема;
б) поток потенциален.
2. Найти составляющие вектора ускорений.
3. Записать вектор ускорения и его модуль.
Задание 3. Составить уравнения вихревых линий, если скорость потока жидкости
, 
, 
.
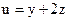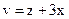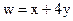Задание 4. Найти функцию тока, если потенциал скоростей
.
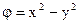Изобразить на графике линии тока и линии равного потенциала.
Задание 5.
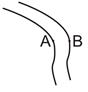Показать, что если река имеет закругление (см. схему), то у берега А уровень ниже, чем у берега В. Считать движение установившимся и безвихревым, зная, что в точке A скорость течения больше, чем в точке В.
Примечание. Использовать интеграл Д. Бернулли.
Задание 6.
1. Записать и доказать свойства осреднения.
2. Записать усредненные по Рейнольдсу уравнения движения в форме Навье (в векторном и скалярном видах).
3. Записать интеграл Бернулли. Дать его энергетическую и геометрическую интерпретацию.
Задание 7.
Определить режим течения воды в трубе диаметром d = 0,05 м, если расход воды Q = 5 л/с и кинематический коэффициент вязкости n = 0,0131 cм2/с (при температуре воды 10 oC).
КОНТРОЛЬНАЯ РАБОТА ПО КУРСУ
Для студентов III курса з/о специальности «Метеорология»
Задание 1. Определить семейство линий тока, а также линию тока, проходящую через точку А (1,1) в момент времени
t = 0. Определить траекторию частицы, которая в момент времени t = 0 находилась в точке A. Задано поле скоростей: u = xt; v = yt;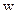 
= 0.
|
|
|
Задание 2. Компоненты поля скорости имеют вид:
, , 
.
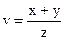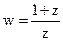1. Определить, будет ли:а) жидкость несжимаема; б) поток потенциален.
2. Найти составляющие вектора ускорений. 
3. Записать вектор ускорения и его модуль.
Задание 3. Составить уравнения вихревых линий, если скорость потока жидкости
, 
, 
.
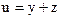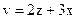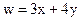Задание 4. Найти функцию тока, если потенциал скоростей
.
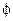
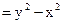Изобразить на графике линии тока и линии равного потенциала.
Задание 5. Определить, как изменится давление в зависимости от скорости течения несжимаемой жидкости в горизонтальной трубе переменного сечения, если движение установившееся и из массовых сил действует только сила тяжести.
Примечание. Использовать интеграл Д. Бернулли.
Задание 6.
1. Записать и доказать свойства осреднения
2. Записать усредненные по Рейнольдсу уравнения движения в форме Навье (в векторном и скалярном видах).
3. Записать интеграл Бернулли. Дать его энергетическую и геометрическую интерпретацию.
Задание 7. Описать и изобразить графически схему возникновения бризов днем и ночью.
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИКИ
Производной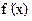 
функции 
называется предел отношения приращения функции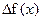 
к приращению аргумента 
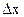, когда приращение аргумента 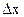стремится к нулю:
.
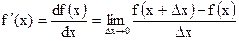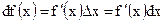, где, как известно, 
;
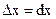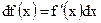– называют дифференциалом функции 
.
Действия вычисления производных и дифференциалов функций называется дифференцированием функций.
Геометрический смысл производной – тангенс угла наклона касательной, проведенной в данной точке графика функции, к положительному направлению оси абсцисс.
Физический смысл производной – скорость изменения функции.
Правила дифференцирования
1. 
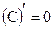, где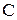 
– константа. Производная от константы равна нулю.
2. 
.
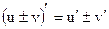3. 
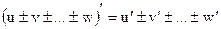. Производная от алгебраической суммы равна той же сумме производных от каждого слагаемого.
4. 
; 
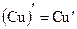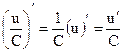. Постоянный множитель можно выносить за знак производной.
|
|
|
5. 
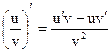. Производная дроби равна дроби, в числителе которой – разность произведений производной числителя на знаменатель и числителя на производную знаменателя, а в знаменателе – квадрат знаменателя.
6. Если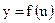 
, а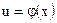 
, т. е. 
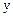есть сложная функция, то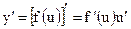 
7. 
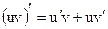. Производная произведения равна сумме произведений производной первого сомножителя на второй без изменения и первого сомножителя на производную от второго сомножителя.
8. 
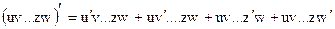– производная произведения нескольких сомножителей.
Примечание. При дифференцировании произведения многих переменных удобнее воспользоваться логарифмическим дифференцированием, а именно, представить
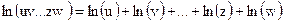, а затем дифференцировать:
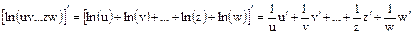
Таблица производных основных элементарных функций
| Простые функции | Сложные функции |
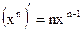 ,  – любое действительное число
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
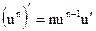
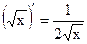
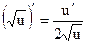
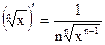
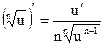
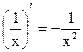
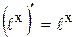
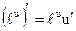
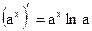
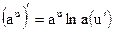
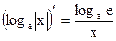
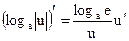
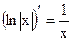
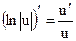
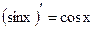
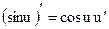
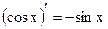
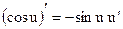
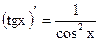
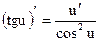
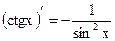
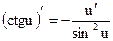
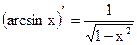
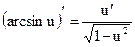
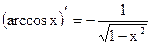
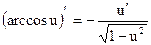
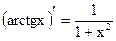
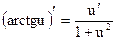
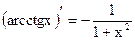
Вычисление производных от производных функций называется повторным дифференцированием: получаем производные второго, третьего и т. д. порядков.
|
|
|
