 |
Принцип нелинейного резонансного усиления. Энергетический выигрыш. Оптимальный угол отсечки.
|
|
|
|
Можно ли осуществить нелинейное резонансное усиление при углах отсечки 730 и 1600. Дать необходимые пояснения.
| Принцип работы нелинейного резонансного усилителя | Баскаков. РТЦиС | Стр. 283-284 |
| Энергетический выигрыш | Баскаков. РТЦиС | Стр. 285 |
| Оптимальный угол отсечки | Баскаков. РТЦиС | Стр. 284 |
Решение задачи:
В усилителях обычно стремятся максимально полно использовать источник питания, приближаясь к границе перенапряженного режима, тогда
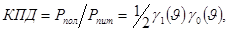
где 
угол отсечки;
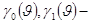функции Берга.
Найдем КПД для двух заданных углов:
С точки зрения эффективности использования источника питания выгоден режим с малым углом отсечки (730).
Вопрос 7
Умножение частоты (определение, схема, временные и спектральные диаграммы, применение). Оптимальный угол отсечки при умножении частоты.
Качественно построить графики временных и спектральных диаграмм, поясняющих умножение в 4 раза.
| Определение | Баскаков. РТЦиС | Стр. 285 (абзац 4) |
| Применение | Баскаков. РТЦиС | Стр. 285 (абзац 5) |
| Оптимальный угол отсечки | Баскаков. РТЦиС | Стр. 285 (последний абзац) - стр. 286 |
Схема и диаграммы.
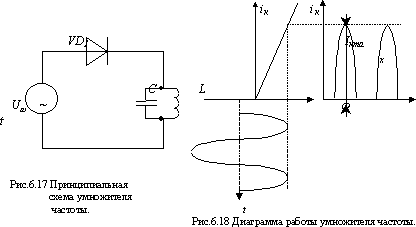
Рассмотрим процесс умножения частоты. Для этой цели используем нелинейный элемент, характеристика которого описывается полиномом 2-ой степени. К нелинейному элементу подводится синусоидальное напряжение:
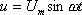
Ток в цепи нелинейного элемента
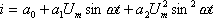
Используя следующее тригонометрические преобразование,
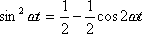
Из этого выражения следует, что ток, протекающий через нелинейный элемент, будет содержать постоянную составляющую, основную частоту w и вторую гармонику 2w. Видно, что степень полинома определяет номер гармоники, т.е. для получения 2-й гармоники необходимо использовать нелинейный элемент с чисто квадратичной характеристикой, описываемой полиномом 2-й степени, и т.д. Для выделения тока n-й гармоники фильтр в цепи нелинейного элемента (параллельный контур) должен быть настроен на частоту n-й гармоники. Спектральный состав тока, протекающего через нелинейный элемент в режиме умножения, показан на рис.6.19.
|
|
|
Однако, при использовании квадратичного (кубического) участка, которое имеет место при умножении слабого сигнала, амплитуда второй и высших гармоник оказывается очень малой. Более целесообразно использовать режим сильного сигнала. В этом случае характеристика нелинейного элемента описывается кусочно-линейной аппроксимацией (рис. 6.19).
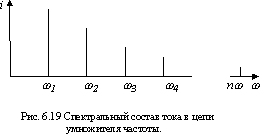
Рабочая точка лежит у изгиба характеристики. Для этой цели к нелинейному элементу должно быть приложено соответствующее отрицательное напряжение смещения. При отрицательных полуволнах входного синусоидального напряжения частотой w нелинейный элемент закрыт. Он открывается только при положительных полуволнах входного напряжения, и ток, протекающий через нелинейный элемент, принимает форму отсеченной косинусоиды. Полученные импульсы целиком определяются двумя величинами - амплитудой импульса тока Imax и углом отсечки q.
Решение задачи:
Пусть на вход цепи умножителя подан сигнал с характеристиками:
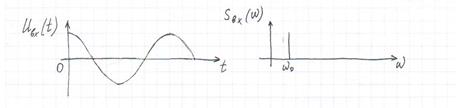
После прохождения через нелинейный элемент характеристики примут вид:
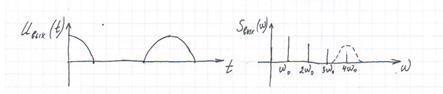
После прохождения через параллельный контур спектральная характеристика примет вид:
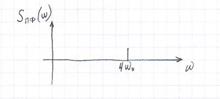
Вопрос 8.
Преобразование частоты (определение, схема, временные и спектральные диаграммы, применение). Преобразование по частоте «вверх», «вниз», их практическое использование в радиотехнических системах (с иллюстрацией в частотной области).
| Определение | Баскаков. РТЦиС | Стр. 308 |
| Схема | Баскаков. РТЦиС | Стр. 309 (Рис. «Схема преобразователя частоты») |
| Описание схемы | Баскаков. РТЦиС | Стр. 308 («Преобразователь частоты состоит из…») |
| Спектральные характеристики | Гоноровский. РТЦиС | Стр. 241 (рис. 8.32) Стр. 242 («В заключение следует…») |
| Применение | Баскаков. РТЦиС | С. 309 (первый абзац) |
|
|
|
Вопрос 9.
Амплитудная модуляция: определение временная функция, временные диаграммы, спектр АМ-сигнала при модуляции простым гармоническим сообщением. Ширина спектра. Определение глубины модуляции по временной и спектральной диаграммам.
Изобразить их графики для глубины модуляции 80%.
| Определение | Баскаков. РТЦиС | Стр.92 |
| Временная функция, временная диаграмма | Баскаков. РТЦиС | Стр. 93-94 |
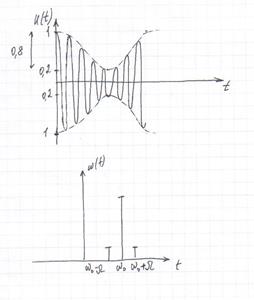
| Спектр АМ-сигнала | Баскаков. РТЦиС | Стр. 94, стр. 96 («Итак, в спектре…») |
Решение задачи:
При амплитудной модуляции связь между огибающей U(t) и модулирующим полезным сигналом s(t) принято определять следующим образом:
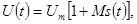
где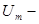 
постоянный коэффициент, равный амплитуде несущего колебания в отсутствие модуляции;
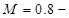коэффициент амплитудной модуляции.
Изобразим графики спектральной и временной диаграмм:
Вопрос 10.
|
|
|
