 |
Случайные процессы, основные определения.
|
|
|
|
Случайными сигналами (процессами) называются сигналы, математическим описанием которых являются случайные функции времени. Случайный процесс представляет собой изменения во времени какой-либо физической величины, которые заранее предсказать невозможно.
Случайной называется функция, значения которой при каждом значении аргумента являются случайными величинами. Случайная функция времени 
, описывающая случайный процесс, в результате опыта может принять ту или иную конкретную форму 
, неизвестную заранее (рис.1). Эти возможные формы случайной функции называются реализациями случайного процесса.В фиксированный момент времени 
значения случайного процесса 
являются случайной величиной с определенным распределением вероятностей. Случайные процессы могут быть непрерывными и дискретными. Реализации первых являются непрерывными функциями времени
Вероятностные характеристики. Если рассматривать не каждую реализацию в отдельности, а совокупность их большого числа, то окажется, что некоторые средние результаты обладают статистической устойчивостью, т.е. могут быть оценены количественно. Устойчивость средних результатов носит вероятностный характер.
Пусть имеется случайный процесс 
, который задан совокупностью N реализации 
(рис. 2). Произведем сечение случайного процесса в некоторый фиксированный момент времени t. Выделим из общего числа N те 
реализаций, значения которых в момент времени 
меньше некоторого уровня 
. При достаточно большом N относительная доля 
реализации, находящихся в момент времени 
ниже уровня , будет обладать статистической устойчивостью, т.е. будет оставаться приблизительно постоянной, колеблясь при изменении N и 
вокруг некоторого среднего значения. Это среднее значение определяет вероятность пребывания значений случайного процесса ниже уровня 
. Функция 
,определяющая вероятность нахождения значений случайного процесса момент времени 
ниже уровня 
, называется одномерной интегральной функцией распределения вероятностей случайного процесса. Ее производная, если она существует, 
называется одномерной плотностью вероятности или дифференциальной функцией распределения случайного процесса.
|
|
|
Введенные функции, и 
дают представление о процессе лишь для изолированных друг от друга моментов времени 
. Для более полной характеристики процесса необходимо учитывать статистическую связь между значениями случайного процесса в различные моменты времени. Эту связь для двух моментов времени учитывает двумерная интегральная функция распределения вероятностей 
определяющая вероятность того, что значения случайного процесса в момент времени 
, будут находиться ниже уровня 
, а в момент времени 
- ниже уровня 
. Частная производная второго порядка 
называется двумерной плотностью вероятностей случайного процесса. Эти функции зависят уже от четырех аргументов.
Аналогично определяются многомерные интегральная и дифференциальная функции распределения случайного процесса
которые зависят от 2 n -аргументов.
Если значения случайного процесса при любых значениях t зависимы, то многомерная функция распределения равна произведению одномерных
(3.1.7)
1. Числовые характеристики случайных сигналов.
Простейшей характеристикой случайного процесса является его среднее значение или математическое ожидание
Дисперсией случайного процесса называется неслучайная функция, значения которой для каждого момента времени t равны, т.е. математическому ожиданию квадрата отклонения случайного процесса от его среднего значения:
|
|
|
Следовательно, дисперсия определяет степень разброса значений случайного процесса около среднего значения. Среднее значение и дисперсия характеризуют поведение случайного процесса в отдельные моменты времени. В качестве характеристики, учитывающей статистическую зависимость между значениями случайного процесса в различные моменты времени, используется корреляционная (иначе - автокорреляционная) функция случайного процесса
определяемая как математическое ожидание от произведения значений процесса в два различных момента времени. Корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени. На рис. 3.5 и 3.6 показаны соответственно два случайных процесса с сильной и слабой статистической зависимостью их значений в моменты времени 
и 
.
Из определения корреляционной функции следует
т.е. она является симметричной относительно начала отсчета времени.
Для совокупности двух случайных и 
статистическая зависимость между их значениями в различные моменты времени определяется функцией взаимной корреляции
В некоторых случаях вместо корреляционной функции вводится нормированная корреляционная функция или кратко коэффициент корреляции
Свойства плотности вероятности и функции распределения.
Баскаков стр. 144
Вопрос 20
F=0 – нет реализаций расположенных ниже плоскости сечения.
F=1 – все реализации лежат ниже плоскости сечения
Вопрос 21
Энергетический спектр случайного процесса, теорема Хинчина-Винера.
Баскаков стр. 164-166
Эффективная ширина спектра, её связь с интервалом корреляции.
Баскаков стр. 169-170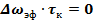 
Широкополосные и узкополосные случайные процессы.
Узкополосный случайный процесс – это такой процесс непрерывный спектр, которого сосредоточен около некоторой фиксированной частоты ω0.
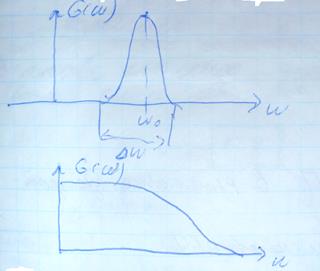
Δω<< ω0 Если данное условие не выполняется, то спектр называется широкополосным.
Функции корреляции таких спектров будут существенно отличаться друг от друга.
Белый шум, его функция корреляции.
Баскаков стр. 170.177
Задача Вопрос 21
Изобразим временные диаграммы случайных процессов ξi(t) и ηj(t)
|
|
|
ξi(t)
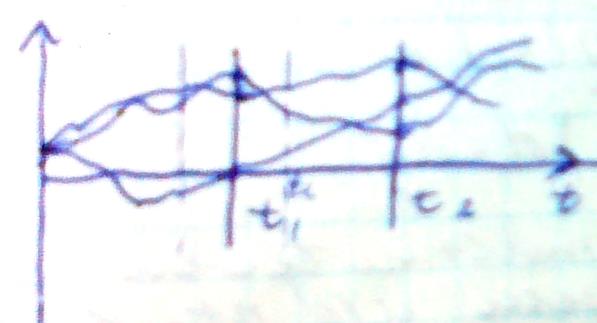
ηj(t)
Как видно из временных диаграмм сигнал ξi(t) изменяется медленно а сигнал ηj(t) изменяется быстрее.
Построим графики G(ω) и B(τ)
B1(τ) функция корреляции сигнала ξi(t)
B2(τ) функция корреляции сигнала ηj(t)
G1(ω) энергетический спектр сигнала ξi(t)
G2(ω) энергетический спектр сигнала ηj(t)
Вопрос № 22
|
|
|
