 |
Метод искусственного принудительного насчёта импульсов в счетчике
|
|
|
|
Теоретические сведения
Счетчики, в зависимости от количества разрядов N, реализуют коэффициент счета 
и их можно использовать в качестве делителей частоты, у которых 
. Часто при проектировании цифровых устройств возникает необходимость в делителях частоты с произвольным коэффициентом счета.
Известны различные методы построения таких делителей. Наиболее широкое распространение получили следующие:
- метод исключения лишних состояний счетчика;
- метод искусственного принудительного насчёта импульсов в счетчике;
- метод принудительного задания коэффициента пересчета в вычитающем счетчике;
- синтез счетчиков с использованием теории цифровых автоматов.
Метод исключения лишних состояний счетчика
Пусть счетчик в процессе счета проходит кодовые комбинации от нулевой до некоторой (N-1)-й, тогда очевидно, что его коэффициент пересчета равен N. Можно уменьшить коэффициент пересчета до значения M< N, исключая часть кодовых комбинаций от M до (N-1). Для этого необходимо сбрасывать счетчик в ноль, как только на его выходе будет установлена комбинация M.
Рассмотрим пример построения делителя, например на 10, на основе стандартной микросхемы К555ИЕ5 (см. рисунок 1.1).
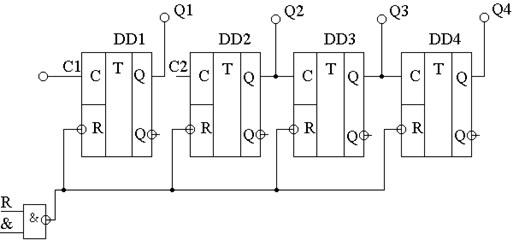
Рисунок 1.1 – Схема делителя на 10
Для k= 10 необходимо соединить Q1 и C2, R и Q4, & и Q2.
Каждый десятый импульс переводит счетчик в состояние 10102, на двух входах элемента 2И-НЕ устанавливаются “1”, и его выходной сигнал сбрасывает все триггеры в “0”. Если один из триггеров DD2 и DD4 сбросится раньше, чем другой, то возможно неполное обнуление счетчика и ошибка в счете. Для увеличения надежности сброса используют дополнительный RS триггер на элементах DD4 и DD5, обеспечивающий сигнал сброса R= 0 вплоть до переднего фронта следующего счетного импульса (см. рисунок 1.2). За это время все разряды счетчика гарантировано устанавливаются в “0”.
|
|
|
Рисунок 1.2 – Схема с дополнительным RS-триггером
Метод искусственного принудительного насчёта импульсов в счетчике
Пусть счётчик, в процессе счёта, проходит кодовые комбинации от нулевой до некоторой (N-1)-й, тогда очевидно, что его коэффициент пересчета равен N. Коэффициент пересчета можно уменьшить до значения M< N, если исключить кодовые комбинации от 0 до К= N-M-1. Для этого необходимо после появления на выходе счетчика комбинации N-1 производить установку триггеров в состояние, соответствующее N-M.
Рассмотрим особенности реализации на счетчиках с последовательным и параллельным переносом.
Алгоритм построения ДПКД на счетчике с последовательным переносом:
1. Разрабатывают счетчик с коэффициентом пересчета M< N.
2. Разрабатывают узел детектирования нулевого состояния счетчика для формирования сигнала установки.
3. Контролируют отсутствие паразитных импульсов в сигнале установки. В случае наличия паразитных импульсов, анализируют времена задержки распространения сигналов, поступающих на входы узла детектирования нулевого состояния, и затем устанавливают элементы задержки по критическим цепям.
4. Заводят сигнал установки на входы S тех триггеров, которые необходимо перевести в единичное состояние.
На рисунках 1.3 и 1.4 показаны ДПКД с коэффициентом пересчета 6 и временные диаграммы его работы.
Рисунок 1.3 – Схема ДПКД с коэффициентом пересчета 6
Рисунок 1.4 – Временные диаграммы работы ДПКД
К особенностям данного ДПКД можно отнести следующее:
- узел детектирования нулевого состояния наиболее просто реализовать на элементах ИЛИ, поскольку в этом случае в выходном сигнале отсутствуют паразитные импульсы;
|
|
|
- длительность сигнала Pset незначительна и зависит от параметров примененной элементной базы, что в ряде случаев может привести к сбоям в работе ДПКД.
Для обеспечения надежности работы ДПКД, импульс Pset следует формировать с помощью дополнительного RS-триггера. В этом случае длительность сигнала Pset равна половине периода сигнала синхронизации (см. рисунки 1.5 и 1.6).
Рисунок 1.5 – Схема ДПКД с коэффициентом пересчета 6 и дополнительным RS-триггером
В счетчиках с параллельным переносом детектируют единичное состояние, и сигнал Pset подают на вход S того триггера, состояние которого не должно измениться по приходу очередного синхросигнала (см. рисунки 1.7 и 1.8).
Из анализа временных диаграмм следует, что длительность сигнала Pset равна периоду входного сигнала синхронизации.
Вариант изменения коэффициента пересчета с установкой комбинации
N-M-1 можно реализовать в счетчиках, имеющих входы предварительной установки, например, на реверсивном счетчике К555ИЕ7 (см. рисунок 1.9).
Он имеет раздельные импульсные тактовые входы для счета на увеличение (+1) и уменьшение (-1) Состояние счетчика изменяется по положительным перепадам тактовых импульсов. Если для счета используется один из этих входов, то на другом тактовом входе следует зафиксировать напряжение высокого уровня.
При подаче “0” на вход LD код, зафиксированный ранее на входах предварительной установки, загружается в счетчик и появляется на его выходах.
Если на вход R подать напряжение “1”, то на всех выходах Qi установится нулевой уровень.
Рисунок 1.6 – Временные диаграммы работы ДПКД с дополнительным
RS-триггером
Рисунок 1.7 – Схема ДПКД с коэффициентом пересчета 6 на счетчике с параллельным переносом
Рисунок 1.8 – Временные диаграммы работы ДПКД на счетчике с параллельным переносом
Рисунок 1.9 – Четырехразрядный реверсивный счетчик с параллельным переносом между разрядами
Сигнал в режиме суммирования на выходе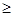 
15 возникает во время перехода из состояния 1111 в 0000.
В режиме вычитания сигнал заёма возникает на выходе 
0 при изменении 0000 на 1111.
Входы предварительной установки могут быть, например, реализованы по схеме, приведенной на рисунке 1.10.
|
|
|
Рисунок 1.10 – Входы предварительной установки
Схема делителя частоты с произвольным коэффициентом деления на микросхеме К555ИЕ7 представлена на рисунке 1.11, а временные диаграммы его работы – на рисунке 1.12.
Рисунок 1.11 – Схема делителя частоты с произвольным коэффициентом деления
Схема отличается простотой, однако выходной код изменяется от N-M до N-1, т.е. отсутствует N-M-1 начальных комбинаций.
Рисунок 1.12 – Временные диаграммы работы ДПКД на микросхеме К555ИЕ7
|
|
|
