 |
Рассмотрим пример косого изгиба.
|
|
|
|
Тема: Сложное сопротивление. Косой изгиб
Понятие о сложном сопротивлении.
На предыдущих лекциях мы рассмотрели простейшие виды деформаций: растяжение-сжатие, сдвиг, кручение, плоский изгиб, поперечный изгиб.
При этом в поперечных сечениях возникает только одно внутреннее усилие - продольная или поперечная сила, крутящий или изгибающий момент, за исключением плоского поперечного изгиба.
| Виды нагружения | Напряжения | Деформации |
 Растяжение Растяжение
|  Условие прочности:
Условие прочности:

|

|
 Сдвиг Сдвиг
| 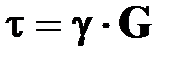 Условие прочности:
Условие прочности:
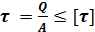
| 
|
 Кручение Кручение
| 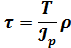 Условие прочности:
Условие прочности:

| 
|
 Изгиб Изгиб
|  Условие прочности:
Условие прочности:
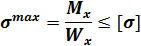
| 

|
На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более.
 Различные комбинации простых деформаций называются сложным сопротивлением.
Различные комбинации простых деформаций называются сложным сопротивлением.
Сегодня приступаем к изучению сложного сопротивления.
В общем случае нагружения бруса в его поперечных сечениях действуют шесть компонентов внутренних усилий (N, Qx, Qy, Mx, My, M кр).
В случае сложного сопротивления в поперечных сечениях элемента возникает два и более внутренних усилия.
При этом расчет элементов при сложном сопротивлении ведется в рамках принципа независимости действия сил. То есть, каждый из простых видов сопротивления, входящих в состав сложного, рассматривается независимо от остальных.
 Затем суммируются полученные решения (для внутренних усилий, напряжений, деформаций и т. д.), т.е. находится суперпозиция полученных решений.
Затем суммируются полученные решения (для внутренних усилий, напряжений, деформаций и т. д.), т.е. находится суперпозиция полученных решений.
Известная нам формулировка принципа суперпозиции или принципа независимости действия сил формулируется следующим образом: напряжение (деформация) от группы сил равно сумме напряжений (деформаций) от каждой силы в отдельности. Он справедлив, если функция и аргумент связаны линейной зависимостью.
|
|
|
 Он становится неприменимым, если:
Он становится неприменимым, если:
- напряжения в какой-либо части конструкции от одной из сил или группы сил превышают предел пропорциональности  ;
;
- деформации или перемещения становятся настолько большими, что нарушается линейная зависимость между ними и нагрузкой.
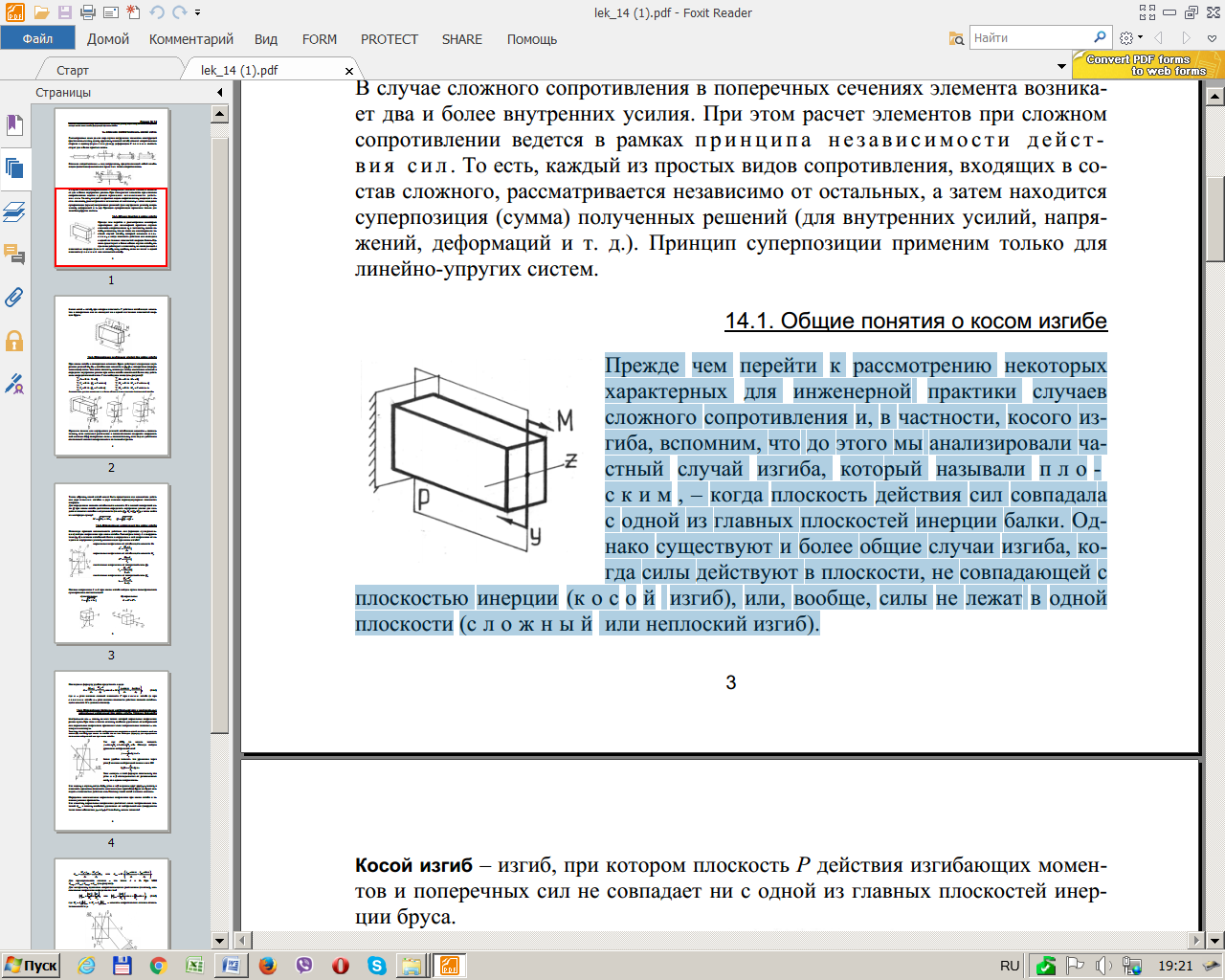
 Мы уже анализировали частный случай изгиба, который называли плоским, – когда плоскость действия сил совпадала с одной из главных плоскостей инерции балки.
Мы уже анализировали частный случай изгиба, который называли плоским, – когда плоскость действия сил совпадала с одной из главных плоскостей инерции балки.
Сегодня начинаем рассматривать более общие случаи изгиба, когда силы действуют в плоскости, не совпадающей с плоскостью инерции (косой изгиб), или, вообще, силы не лежат в одной плоскости (сложный или неплоский изгиб).
Различают:
- косой изгиб или изгиб в двух плоскостях
- межцентровое растяжение – сжатие
 - изгиб с кручением.
- изгиб с кручением.
Общие понятия о косом изгибе. Определение внутренних усилий при косом изгибе.
Дадим определение
Косой изгиб– изгиб, при котором плоскость действия нагрузок (изгибающих моментов, поперечных сил, РРН) не совпадает ни с одной из главных плоскостей сечения бруса.
При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: M x, My – изгибающие моменты и Q x, Q y – поперечные (перерезывающие) силы.
Это легко показать, используя метод сечений и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце.
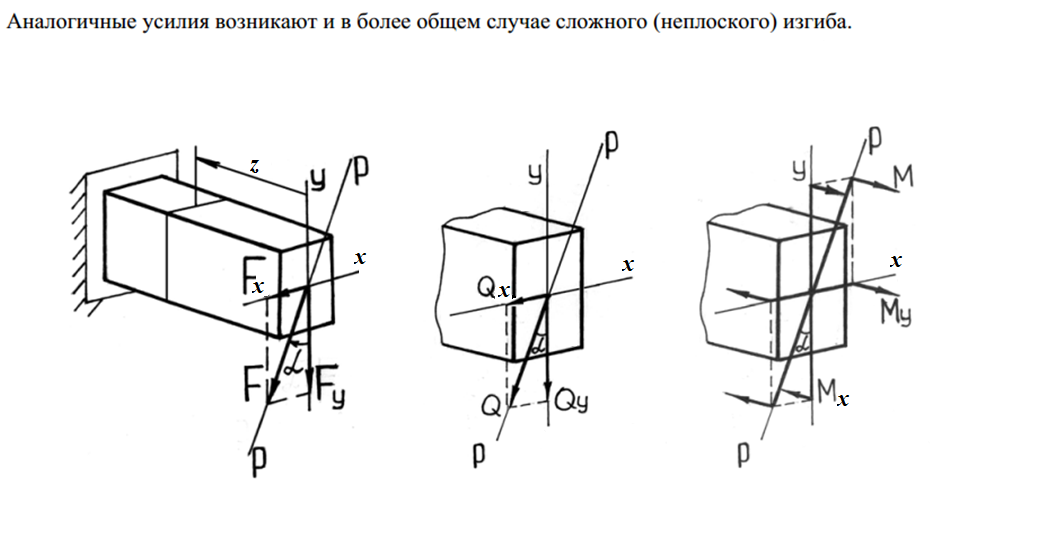
Рассмотрим пример косого изгиба.
Пусть на консольную балку прямоугольного сечения действует сила F, приложенная в плоскости его торцевого поперечного сечения таким образом, что ее линия действия составляет угол α с главной центральной осью OY.
|
|
|
Разложим эту силу на составляющие Fx и F у по главным осям ОХ и ОУ.


Каждая из этих составляющих вызывает прямой изгиб бруса в одной из главных плоскостей.
Сила Fx – в плоскости zOx и сила F у в плоскости zOy.
Следовательно косой изгиб можно рассматривать как совокупность двух прямых изгибов во взаимноперпендикулярных плоскостях, проходящих через главные центральные оси.
Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы x Oy; поперечные силы– положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.
Применим метод сечений и рассмотрим равновесие отсеченной части бруса.
В произвольном сечении бруса возникают два изгибающих момента: My относительно главной оси Ох и Mx относительно главной оси О y


 Получаем ВСФ
Получаем ВСФ
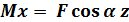

Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Q x, M x и Q y, My), а затем найти их векторную сумму:


|
|
|


