 |
Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу.
|
|
|
|
Например, верхний ряд знаков «+» и «—» соответствует напряжениям от Мx , а нижний ряд — от My
| y |
| x |
| + - |
| - |
| + - |
| + - |
| + - |
| - |
| - |
| - |
| А - |
| В - |
| D - |
| C - |
Точка А от Мx верхняя сила растягивает волокна, а нижняя сжимает, ставим знак плюс, от My левая сила сжимает волокна, а правая растягивает - ставим знак минус.
Точка В от Мx верхняя сила растягивает волокна, а нижняя сжимает, ставим знак плюс,от My левая сила сжимает волокна, а правая растягивает - ставим знак плюс
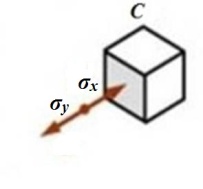Точка C от Мx нижняя сжимает сила волокна, а верхняя растягивает, ставим знак минус, от My левая сила сжимает волокна, а правая растягивает - ставим знак плюс.
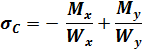
Точка D от Мx нижняя сила сжимает волокна, а верхняя растягивает, ставим знак минус, от My левая сила сжимает растягивает волокна, а правая растягивает ставим знак минус.
Из рисунка следует, что опасными являются точки, в которых складываются напряжения – B и D.
Пример 3
Напряжения точках A, B, C, D будут равны:
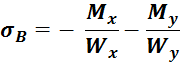
В случае поперечных сечений (прямоугольник сплошной и полый, двутавр) имеющих две оси симметрии и выступающие угловые точки с равными по модулю и максимальными одноименными координатами:
Напряжения в точках будут равны
При проведении расчетов на прочность условие прочности составляется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений.
Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.
|
|
|
В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.
Положение нейтральной оси при косом изгибе.
Нулевой или нейтральной линией называется геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю.
В точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.
Заметим, что при плоском изгибе нейтральная ось совпадала с одной из главных осей сечения (Oy или Oх), при косом же изгибе это не так.
Обозначим угол отклонения нейтральной оси от ох – β.
Обозначим хо и уо, положение точки О, принадлежащей нейтральной линии.
Выведем формулу для определения положения нейтральной оси при косом изгибе.
Положив σ =0, получим уравнение нейтральной линии.
Или
Найдем угол наклона нейтральной линии, из рисунка видно:
Следовательно:
Уравнение нейтральной оси:
Знак«минус» в этой формуле показывает, что углы α и β откладываются от разноименных осей, но в одном направлении.
Анализируя полученное выражение, приходим к выводу, что в отличие от прямого изгиба нулевая и силовая линии не будут взаимно перпендикулярны
Лишь в частном случае, когда 
, угол между нулевой и силовой линиями будет прямым.
Нулевая и силовая линии проходят через разные квадранты сечений
Свойства нейтральной линии
1. Если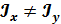 
, то 
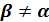, то есть силовая плоскость и нейтральная линия не являются перпендикулярными.
2. Если , то 
, то есть нейтральная линия и силовая плоскость перпендикулярны. В этом случае стержень испытывает плоский изгиб (примерами таких стержней являются стержни с сечением – круг, кольцо, квадрат).
|
|
|
3. Знак «минус» в формуле указывает, что силовая плоскость и нейтральная линия при косом изгибе проходят через противоположные квадранты.
Для определения опасных точек сечения следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными.
Пример 4
|
|
|
