 |
Рассмотрим распределение напряжений по поперечному сечению бруса.
|
|
|
|
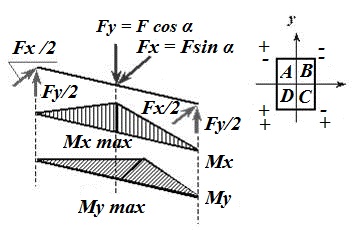
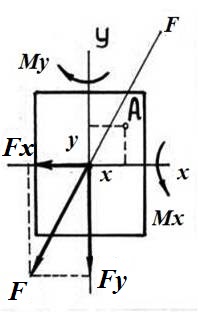Эпюра I показывает распределение напряжений от силы Fу (соответствующих моменту Мх), эпюра II – напряжений от силы Fx ( соответствующих моменту My,) аэпюра III суммарных напряжений
По эпюрам I и II легко установить в какую строрну от оси х должен быть отложен угол β, нейтральная ось должна пройти через те четверти (квадранты) сечения, в которых знаки составляющих напряжений различны. В рассматириваемом случае через 2 и 4 четверти.
| y |
| x |
| + - |
| - |
| + - |
| + - |
| + - |
| - |
| - |
| - |
| А - |
| В - |
| D - |
| C - |
Условие прочности при косом изгибе..
Условие прочности для балок из пластичного материала для сечений типа прямоугольник, двутавр, швеллер запишется в виде:
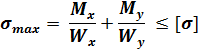
Или
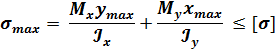
6. 
Определение перемещений при косом изгибе.
Перемещения при косом изгибе определяют по принципу независимости действия сил, т.е. рассчитывают прогибы f х и f у в направлении главных осей, а величину полного прогиба в любом сечении балки получают геометрическим суммированием:
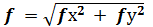
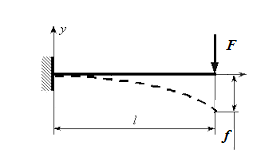
Например, для бруса защемленного одним концом и нагруженного силой на свободном конце, прогиб конца консоли определится следующим образом:
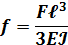
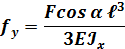
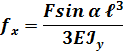
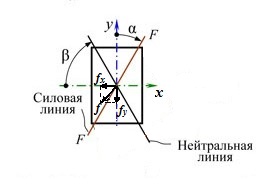
Направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы.
Определим направление полного прогиба
где β угол между направлением полного прогиба и осью ох.
|
|
|
При плоском косом изгибе направление полного прогиба перпендикулярно к нулевой линии.
Три типа задач расчета конструкций на прочность при косом изгибе.
1. Поверочный расчет - проверка прочности;
2. Проектный расчет или проектировочный расчет - подбор сечения [определить Wx (размеры сечения), при заданном отношении Wx / Wy ];
3. Определение грузоподъемности - проверка по несущей способности (определить M).
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе.
Для этого необходимо:
- построить эпюры внутренних усилий (изгибающих моментов).
Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие.
- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;
- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
- записать условие прочности в этих точках.
Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.
Пример 1.
Подобрать прямоугольное сечение балки при условии, что h = 2 b,[σ]= 160 МПа P = 60кН, α =30 ͦ, ℓ=2,8 м..
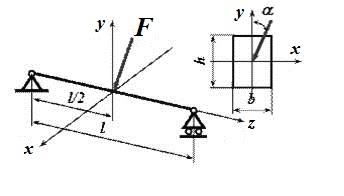
Решение:α
Разложив силу F на две составляющие, действующие по направлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов M x и M y. Наибольшие моменты действуют в среднем сечении, где
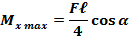
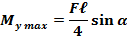
следовательно, это сечение является опасным.
Эпюры изгибающих моментов к примеру 1
Для определения положения опасной точки расставим знаки от σ (Mx) и σ (My) в угловых точках поперечного сечения балки.
При действии момента Mx в точках D и C будут иметь место положительные (растягивающие) напряжения, а в точках A и B - отрицательные (сжимающие) напряжения. При действии момента My в точках A и D будут иметь место положительные напряжения, а в точках B и C - отрицательные.
|
|
|
Точки поперечного сечения D и B, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.
Судя по условию задачи, материал, из которого изготовлена балка, является пластичным ([ σ ]=160 МПа) и, следовательно, одинаково сопротивляется деформации растяжения и деформации сжатия.
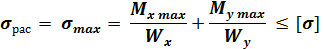
Вычислим моменты сопротивления сечения при заданном соотношении высоты и ширины
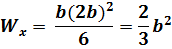
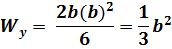
Подставляя в условие прочности выражения для изгибающих моментов и моментов сопротивления, получим:
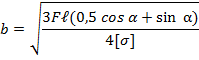
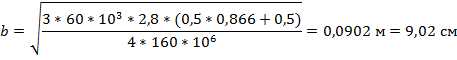
тогда h = 2 b = 18,04 см.
|
|
|
