 |
Закон распределения непрерывной
|
|
|
|
Цифровой сигнал
Цифровой сигнал - сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.
Сигналы представляют собой дискретные электрические или световые импульсы. При таком способе вся емкость коммуникационного канала используется для передачи одного сигнала. Цифровой сигнал использует всю полосу пропускания кабеля. Полоса пропускания - это разница между максимальной и минимальной частотой, которая может быть передана по кабелю. Каждое устройство в таких сетях посылает данные в обоих направлениях, а некоторые могут одновременно принимать и передавать. Узкополосные системы (baseband) передают данные в виде цифрового сигнала одной частоты.
Дискретный цифровой сигнал сложнее передавать на большие расстояния, чем аналоговый сигнал, поэтому его предварительно модулируют на стороне передатчика, и демодулируют на стороне приёмника информации. Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.
Замечание. Следует иметь в виду, что реальный цифровой сигнал по своей физической природе является аналоговым. Из-за шумов и изменения параметров линий передачи он имеет флуктуации по амплитуде, фазе/частоте (джиттер), поляризации. Но этот аналоговый сигнал (импульсный и дискретный) наделяется свойствами числа. В результате для его обработки становится возможным использование численных методов (компьютерная обработка).
Дискретность (от лат. discretus - разделенный, прерывистый) - прерывность; противопоставляется непрерывности. Напр., дискретное изменение к.-л. величины во времени - это изменение, происходящее через определенные промежутки времени (скачками); система целых (в противоположность системе действительных чисел) является дискретной.
|
|
|
Дискретный сигнал - сигнал, параметр которого принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы).
2. Что представляет собой ортогональный базис Котельникова и каковы его свойства? С.123
Теорема Котельникова
Теорема Котельникова (иногда в зарубежной литературе теорема Найквиста) позволяет выделить класс сигналов, для которых эти сигналы могут быть без потерь информации представлены своими дискретными отсчетами. Мы уже видели, что если в спектре аналоговой сигнала не содержится составляющих с частотами выше частоты Найквиста, то сдвинутые копии спектров не будут прерываться. В этом случае использование идеального ФНЧ с прямоугольной АЧХ позволит выделить исходную (несдвинутую) копию спектра, сосредоточенную в окрестности нулевой частоты и, таким образом, в точности восстановить исходный аналоговый сигнал. 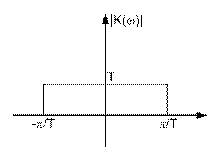 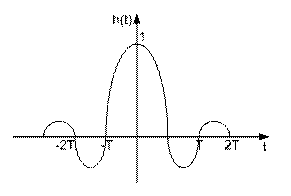 АЧХ идеального ФНЧ для восстановления показана на рисунке. Коэффициент передачи ФНЧ в полосе пропускания равен Т, а не единице, чтобы скомпенсировать множитель 4Т в формуле спектра. С помощью обратного преобразования Фурье находим импульсную характеристику фильтра АЧХ идеального ФНЧ для восстановления показана на рисунке. Коэффициент передачи ФНЧ в полосе пропускания равен Т, а не единице, чтобы скомпенсировать множитель 4Т в формуле спектра. С помощью обратного преобразования Фурье находим импульсную характеристику фильтра 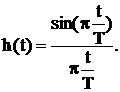 Дискретизованный сигнал – это сумма дельта-функций. При прохождении такого сигнала через восстанавливающий фильтр НЧ каждая дельта-функция породит на выходе соответственно сдвинутую и масштабированную копию импульсной характеристики фильтра. Выходной сигнал (в точности соответствующий исходному аналоговому сигналу) будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик идеального ФНЧ Дискретизованный сигнал – это сумма дельта-функций. При прохождении такого сигнала через восстанавливающий фильтр НЧ каждая дельта-функция породит на выходе соответственно сдвинутую и масштабированную копию импульсной характеристики фильтра. Выходной сигнал (в точности соответствующий исходному аналоговому сигналу) будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала копий импульсных характеристик идеального ФНЧ  Сформулируем теорему Котельникова: любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторого значения?в = 2?fв (сигнал с финитным, т.е. конечным спектром) может быть без потерь информации представлен своими отсчетами {s(kT)}, взятыми с интервалом Т, удовлетворяющим следующему равенству Сформулируем теорему Котельникова: любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторого значения?в = 2?fв (сигнал с финитным, т.е. конечным спектром) может быть без потерь информации представлен своими отсчетами {s(kT)}, взятыми с интервалом Т, удовлетворяющим следующему равенству 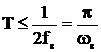 В зарубежной литературе эта теорема называется теоремой Найквиста (Nyquist Theorem) или теоремой дискретизации, теоремой о выборке (sampling theorem). Последняя формула представляет собой разложение сигнала s(t) в ряд по системе функций {?k(t)}, называемой базис Котельникова В зарубежной литературе эта теорема называется теоремой Найквиста (Nyquist Theorem) или теоремой дискретизации, теоремой о выборке (sampling theorem). Последняя формула представляет собой разложение сигнала s(t) в ряд по системе функций {?k(t)}, называемой базис Котельникова  Заметим, что функции всегда Заметим, что функции всегда 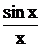 называются sinc-функциями. называются sinc-функциями.
|
Теорема Котельникова
|
|
|
В 1933 году В.А. Котельниковым доказана теорема отсчетов [6, 32], имеющая важное значение в теории связи: непрерывный сигнал  с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам
с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам  , взятым через интервалы
, взятым через интервалы 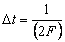 , где
, где  – верхняя частота спектра сигнала.
– верхняя частота спектра сигнала.
В соответствии с этой теоремой сигнал  можно представить рядом Котельникова [6, 32]:
можно представить рядом Котельникова [6, 32]:
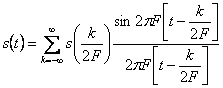 . .
| (1.21) |
Таким образом, сигнал  , можно абсолютно точно представить с помощью последовательности отсчетов
, можно абсолютно точно представить с помощью последовательности отсчетов 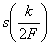 , заданных в дискретных точках
, заданных в дискретных точках 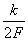 (рис.1.16).
(рис.1.16).

Функции
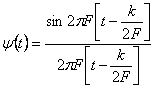
| (1.22) | |
образуют ортогональный базис в пространстве сигналов, характеризующихся ограниченным спектром:
| (1.23) |
Обычно для реальных сигналов можно указать диапазон частот, в пределах которого сосредоточена основная часть его энергии и которым определяется ширина спектра сигнала. В ряде случаев спектр сознательно сокращают. Это обусловлено тем, что аппаратура и линия связи должны иметь минимальную полосу частот. Сокращение спектра выполняют, исходя из допустимых искажений сигнала. Например, при телефонной связи хорошая разборчивость речи и узнаваемость абонента обеспечиваются при передаче сигналов в полосе частот 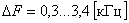 . Увеличение
. Увеличение 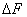 приводит к неоправданному усложнению аппаратуры и повышению затрат. Для передачи телевизионного изображения при стандарте в 625 строк полоса частот, занимаемая сигналом, составляет около 6 МГц.
приводит к неоправданному усложнению аппаратуры и повышению затрат. Для передачи телевизионного изображения при стандарте в 625 строк полоса частот, занимаемая сигналом, составляет около 6 МГц.
Из вышесказанного следует, что процессы с ограниченными спектрами могут служить адекватными математическими моделями многих реальных сигналов.
Функция вида 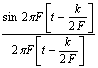 называется функцией отсчетов (рис.1.17).
называется функцией отсчетов (рис.1.17).
|
|
|
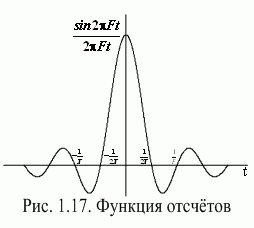 Она характеризуется следующими свойствами. Если
Она характеризуется следующими свойствами. Если  , функция отсчетов имеет максимальное значение при
, функция отсчетов имеет максимальное значение при  , а в моменты времени
, а в моменты времени  (
( ) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне равна
) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне равна 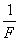 , поэтому минимальная длительность импульса, который может существовать на выходе линейной системы с полосой пропускания
, поэтому минимальная длительность импульса, который может существовать на выходе линейной системы с полосой пропускания  , равна
, равна 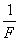 ; функции отсчетов ортогональны на бесконечном интервале времени.
; функции отсчетов ортогональны на бесконечном интервале времени.
На основании теоремы Котельникова может быть предложен следующий способ дискретной передачи непрерывных сигналов:
Для передачи непрерывного сигнала  по каналу связи с полосой пропускания
по каналу связи с полосой пропускания  определим мгновенные значения сигнала
определим мгновенные значения сигнала  в дискретные моменты времени
в дискретные моменты времени  , (
, ( ). После этого передадим эти значения по каналу связи каким - либо из возможных способов и восстановим на приемной стороне переданные отсчеты. Для преобразования потока импульсных отсчетов в непрерывную функцию пропустим их через идеальный ФНЧ с граничной частотой
). После этого передадим эти значения по каналу связи каким - либо из возможных способов и восстановим на приемной стороне переданные отсчеты. Для преобразования потока импульсных отсчетов в непрерывную функцию пропустим их через идеальный ФНЧ с граничной частотой  .
.
Можно показать, что энергия сигнала находится по формуле [6, 32]:
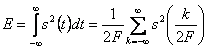 . .
| (1.24) |
Для сигнала, ограниченного во времени, выражение (1.24) преобразуется к виду:
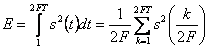 . .
| (1.25) |
Выражение (1.25) широко применяется в теории помехоустойчивого приема сигналов, но является приближенным, т.к. сигналы не могут быть одновременно ограничены по частоте и времени.
3. Как получить коэффициенты разложения сигнала в базисе Котельникова?
Фундаментальное значение для решения многих задач теории передачи сигналов имеет следующая теорема Котельникова: непрерывная функция времени
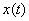 , не содержащая частот выше граничной сов, полностью определяется отсчетами мгновенных значений
, не содержащая частот выше граничной сов, полностью определяется отсчетами мгновенных значений  в точках, отстоящих друг от друга на интервалы
в точках, отстоящих друг от друга на интервалы  . Интервал
. Интервал 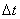 часто называют интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию
часто называют интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию 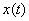 в виде ряда:
в виде ряда:
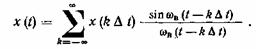 (1.69)
(1.69)
Из сопоставления ряда (1.69) с общим видом ортогонального разложения
 (1.70)
(1.70)
следует, что элементарными функциями в разложении Котельникова являются функции
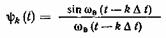 (1.71)
(1.71)
называемые функциями отсчетов.
|
|
|
Ортогональность этих функций (1.71) следует непосредственно из соотношения
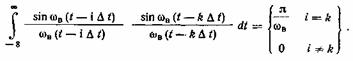
В соответствии с (1.16) коэффициенты 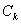 ортогонального разложения (1.70) в общем виде определяются выражением
ортогонального разложения (1.70) в общем виде определяются выражением
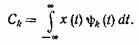 (1.72)
(1.72)
В частном случае, для коэффициентов разложения (1.70) по элементарным функциям (1.71) можем записать
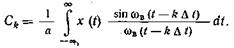 (1.73)
(1.73)
Покажем теперь, что 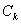 действительно мгновенные значения функции
действительно мгновенные значения функции 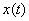 в момент
в момент  . Действительно, для функции с ограниченным спектром
. Действительно, для функции с ограниченным спектром
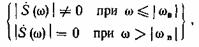
поэтому для преобразования Фурье можем записать
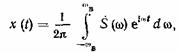 (1.74)
(1.74)
где

Преобразование (1.74) дает возможность определить функцию времени 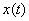 для любого момента времени t, в том числе и для интересующего нас момента
для любого момента времени t, в том числе и для интересующего нас момента  :
:

или после подстановки в последнее выражение вместо  его значения из (1.74) и изменения порядка интегрирования получим
его значения из (1.74) и изменения порядка интегрирования получим
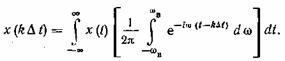 (1.75)
(1.75)
После вычисления интеграла в квадратных скобках
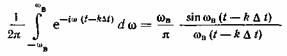
выражение (1.75) принимает вид
 (1.76)
(1.76)
Сравнение (1.76) с (1.73) при 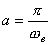 показывает, что полученные отсчеты
показывает, что полученные отсчеты  функции
функции 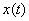 в моменты
в моменты  являются коэффициентами Фурье
являются коэффициентами Фурье 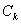 разложения (1.70) по ортогональным функциям (1.71) и потому полностью определяют функцию
разложения (1.70) по ортогональным функциям (1.71) и потому полностью определяют функцию 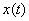 . Ряд (1.70) сходится к функции
. Ряд (1.70) сходится к функции 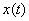 .
.
Таким образом, если известны значения функции 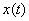 в точках отсчетов
в точках отсчетов  , то она может быть полностью восстановлена для всех t суммированием элементарных функций отсчетов (1.71) с соответствующими коэффициентами
, то она может быть полностью восстановлена для всех t суммированием элементарных функций отсчетов (1.71) с соответствующими коэффициентами  . Графики функций (1.71) для
. Графики функций (1.71) для  представлены на рис. 1.15 б: ось симметрии каждой функции вида
представлены на рис. 1.15 б: ось симметрии каждой функции вида 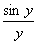 приходится на момент времени
приходится на момент времени  , где функции (1.71) обращаются в единицу; в моменты же времени
, где функции (1.71) обращаются в единицу; в моменты же времени 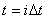 (при
(при 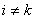 ) функция (1.71) равна нулю. Следовательно, сумма (1.69) дает значения функции
) функция (1.71) равна нулю. Следовательно, сумма (1.69) дает значения функции  , поскольку все остальные члены суммы в этот момент равны нулю. Из (1.69) следует и процедура восстановления функции
, поскольку все остальные члены суммы в этот момент равны нулю. Из (1.69) следует и процедура восстановления функции 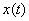 по отсчетам
по отсчетам  : нужно перемножить значения отсчетов
: нужно перемножить значения отсчетов  на соответствующие от счетные функции (1.71) и просуммировать полученные произведения (рис. 1.15 в). Для полного восстановления непрерывной функции
на соответствующие от счетные функции (1.71) и просуммировать полученные произведения (рис. 1.15 в). Для полного восстановления непрерывной функции 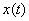 по значениям ее отсчетов нужно просуммировать бесконечное множество членов ряда (1.69).
по значениям ее отсчетов нужно просуммировать бесконечное множество членов ряда (1.69).
4. Что утверждает торема Котельникова? С. 122-123
В 1933 году В.А. Котельниковым доказана теорема отсчетов [6, 32], имеющая важное значение в теории связи: непрерывный сигнал  с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам
с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам  , взятым через интервалы
, взятым через интервалы 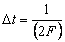 , где
, где  – верхняя частота спектра сигнала.
– верхняя частота спектра сигнала.
5. В чём сущность временной дискретизации, где она может применяться и с
какой целью?
Дискретизация - преобразование непрерывной функции в дискретную. При дискретизации только по времени, непрерывный аналоговый сигнал заменяется последовательностью отсчётов, величина которых может быть равна значению сигнала в данный момент времени. Возможность точного воспроизведения такого представления зависит от интервала времени между отсчётами Δt. Согласно теореме Котельникова:
|
|
|

где 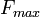 - наибольшая частота спектра сигнала
- наибольшая частота спектра сигнала
Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике - по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике - по вертикали).
Сигнал, к которому применены дискретизация и квантование, называется цифровым.
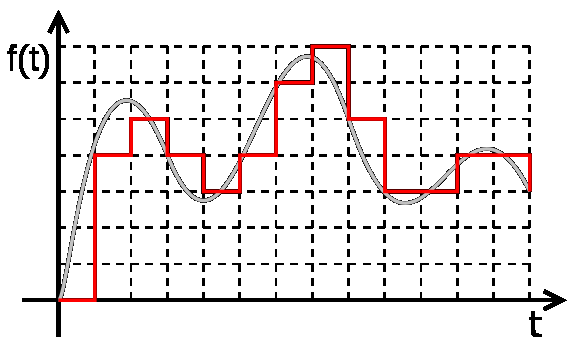
Рисунок 3 - Цифровой сигнал
Этапы дискретизации
Область определения функции разбивается точками x1, x2,., xn на отрезки равной длины и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке; полученная на этом этапе функция называется ступенчатой. Следующий шаг - проецирование значений "ступенек" на ось значений функции (ось ординат). Полученная таким образом последовательность значений функции y1, y2,., yn является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать путем уменьшения длин отрезков разбиения области значений аргумента.
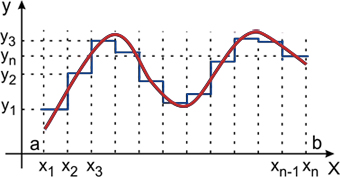
Рисунок 4 - Дискретизация
Ось значений функции можно разбить на отрезки с заданным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений. В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков.
Таким образом, любое сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер - цифровая машина, т.е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.
6. В чём состоят принципиальные трудности восстановления сигнала после
дискретизации в реальных условиях? С.124
Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит, что, если аналоговый сигнал  имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной верхней частоты
имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной верхней частоты 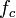 :
:

Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой 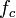 ».
».
Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и, обычно, имеют во временно́й характеристике разрывы. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают 2 следствия:
- Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой
 , где
, где 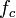 — максимальная частота, которой ограничен спектр реального сигнала.
— максимальная частота, которой ограничен спектр реального сигнала.
- Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.
7. Как восстановить исходный сигнал по его отсчетам?
Передискретиза́ция (англ. resampling) в обработке сигналов — изменение частоты дискретизации дискретного (чаще всего цифрового) сигнала.
Отсчёты сигнала, соответствующие новой частоте дискретизации, вычисляются по уже имеющимся отсчётам и не содержат новой информации.
Повышение частоты дискретизации называется интерполяцией, понижение — децимацией. [1]
Согласно теореме Котельникова любой непрерывный сигнал с финитным спектром (то есть таким спектром, в котором спектральные составляющие, соответствующие частотам выше или равным некоторой частоты f 0, отсутствуют) может быть представлен в виде отсчётов дискретного сигнала с частотой дискретизации fd > 2 f 0. При этом такое преобразование является взаимно однозначным, то есть при соблюдении условий теоремы Котельникова по дискретному сигналу можно восстановить исходный сигнал с финитным спектром без искажений.[2]
При передискретизации отсчёты сигнала, соответствующие одной частоте дискретизации, вычисляются по имеющимся отсчётам этого же сигнала, соответствующим другой частоте дискретизации (при этом предполагается, что обе частоты дискретизации соответствуют условиям теоремы Котельникова). Идеальная передискретизация эквивалентна восстановлению непрерывного сигнала по его отсчётам с последующей дискретизацией его на новой частоте.[3]
Точное вычисление значения исходного непрерывного сигнала в определённой точке производится следующим образом:[4][5]
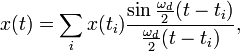
где x (ti) — i-й отсчёт сигнала, ti — момент времени, соответствующий этому отсчёту, ω d = 2π fd — циклическая частота дискретизации, x (t) — интерполированное значение сигнала в момент времени t.
Функция  не является финитной, поэтому для вычисления значения сигнала в определённый момент времени с помощью вышеприведённого выражения необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем), что нереализуемо на практике. В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид:[6][7]
не является финитной, поэтому для вычисления значения сигнала в определённый момент времени с помощью вышеприведённого выражения необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем), что нереализуемо на практике. В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид:[6][7]

где h (t) — импульсная характеристика соответствующего восстанавливающего фильтра. Вид этого фильтра выбирается в зависимости от задачи.[8]
Прямое вычисление новых отсчётов сигнала по вышеприведённым формулам требует значительных вычислительных ресурсов и нежелательно для приложений реального времени. Существуют важные частные случаи передискретизации, для которых вычисление новых отсчётов производится проще:[9]
- децимация с целым коэффициентом (уменьшение частоты дискретизации в целое число раз);
- интерполяция с целым коэффициентом (увеличение частоты дискретизации в целое число раз);
- изменение частоты дискретизации в рациональное (M / N) число раз (этот случай можно рассматривать как комбинацию двух предыдущих).
При таких ограничениях становится удобным применение стандартных реализаций цифровых фильтров для передискретизации.
8. Как получить амлитудно-импульсную модуляцию?
Амплитудно-импульсная модуляция (АИМ) заключается в изменении приращения амплитуды импульсов пропорционально функции управляющего сигнала при постоянной длительности импульсов и периоде их следования:
U(t) = Uo + k·s(t), wи = const, T = const. (15.4.1)
Спектр АИМ рассмотрим на примере модулирования однотонального сигнала s(t), приведенного на рис. 15.4.1. Напишем уравнение модулированного сигнала в следующей форме:
u(t) = (1+M cos wt)·f(t), (15.4.2)
где f(t) – периодическая последовательность прямоугольных импульсов с частотой wo, которую можно аппроксимировать рядом Фурье (без учета фазы):
f(t) = Uo + 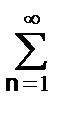 Un cos nwot. (15.4.3)
Un cos nwot. (15.4.3)
Подставляя (15.4.3) в (15.4.2), получаем:
u(t) = (1+M cos wt)Uo+ 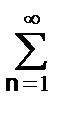 Un cos nwot ·(1+M cos wt)
Un cos nwot ·(1+M cos wt)
u(t) = Uo + UoM cos wt + 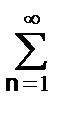 Un cos nwot +
Un cos nwot +
+ 0.5M 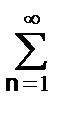 Un cos (nwo+w)t + 0.5M
Un cos (nwo+w)t + 0.5M 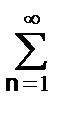 Un cos (nwo-w)t. (15.4.2)
Un cos (nwo-w)t. (15.4.2)
Форма спектра, в начальной части спектрального диапазона, приведена на рис. 15.4.1. В целом, спектр бесконечен, что определяется бесконечностью спектра прямоугольных импульсов. Около каждой гармоники nwo спектра прямоугольных импульсов появляются боковые составляющие nwo±w, соответствующие спектру моделирующей функции (при многотональном сигнале – боковые полосы спектров). При дополнительном высокочастотном заполнении импульсов весь спектр смещается в область высоких частот на частоту заполнения.

Рис. 15.4.1.
9. От чего зависит ширина спектра АИМ-сигнала?
Ширина спектра АИМ – сигнала:
ΔFАИМ= α / τи, где α от 3 до 5
коэффициент α зависит от формы импульсов.
Работа 3
1. Дайте определение понятия "случайный процесс»?
В реальных условиях при передаче информации сигнал в месте приема заранее неизвестен и потому не может быть описан определенной функцией времени. То же самое можно сказать и о помехах, появление которых обусловлено самыми различными и чаще всего неизвестными причинами.
Таким образом, реальные сигналы и помехи представляют собой случайные процессы. Случайный процесс описывается случайной функцией, значения которой при любом значении аргумента являются случайными величинами. В отличие от детерминированной функции, однозначно определяющей и, таким образом, достоверно предсказывающей значение описываемой величины в любой заданный момент времени, ход случайной функции предсказан быть не может. Самое большое, что можно сказать заранее о поведении случайной функции — это вероятность, с которой она в будущем может принять тот или иной вид из множества возможных.
В ряде практически важных задач случайный процесс наряду с вероятностным описанием можно описать совокупностью неслучайных числовых характеристик, постоянных или меняющихся во времени. От этих характеристик требуется, чтобы в условиях конкретно поставленной задачи они отражали самое существенное случайного процесса.
2. В чём разница между понятиями "случайный процесс" и "случайная
реализация"?
Под опытом или испытанием понимается, например, однократное включение источника случайного процесса на некоторое определенное время с соответствующей записью колебания. В результате многократного повторения опыта с данным источником можно получить множество реализаций процесса, внешне совершенно не похожих одна на другую. Для получения реализаций процесса таким путем необходима повторяемость условий испытаний. Во многих случаях повторяемость условий испытаний единственного источника не может быть соблюдена, так как параметры источника необратимо меняются во времени. В этих условиях следует оперировать понятием не единственного источника, а их множества. В результате опыта, предусматривающего параллельную работу источников, получаем множество реализаций. При этом источники могут быть неидентичными, их параметры имеют разброс и меняются во времени.
Случайный процесс полностью характеризуется бесконечным множеством реализаций, образующих ансамбль. Понятием ансамбля, состоящего из бесконечно большого или конечного, но достаточно большого числа реализаций (рис. 2.22), удобно пользоваться при установлении статистических закономерностей, свойственных случайным процессам. Совокупность мгновенных значений случайного процесса, заданного ансамблем, в произвольный момент времени называют сечением случайного процесса.
Если зафиксировать произвольный момент времени t1, т. е. получить сечение случайного процесса, то для этого сечения может быть вычислено распределение вероятности Ð(ŏ) непрерывной случайной величины Õ (t1):


3. Какие случайные процессы называются стационарными? С. 157-158
Так принято называть случайные процессы, статистичесие характеристики которых одинаковы во всех сечениях. Говорят, что случайный процесс стационарен в узком смысле, если любая его n-мерная плотность вероятности инвариантна относительно временного сдвига τ.
Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. Теория стационарных случайных функций разработана наиболее полно и для ее использования обычно достаточно определения стационарности в широком смысле: случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.
4. В чём состоит свойство эргодичности? С. 158-159
Стационарный случайный процесс называют эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени. Операция усреднения выполняется над единственной реализацией х(t), длительность Т которой теоретически может быть сколь угодно велика.
5. Как связаны между собой плотность распределения вероятности,
функция распределения и характеристическая функция случайной
величины?
Закон распределения непрерывной
Случайной величины
Для непрерывной случайной величины невозможно задать закон
распределения в том виде, в каком он задается для дискретной величины,
поскольку непрерывная случайная величина имеет бесконечное множест-
во возможных значений, сплошь заполняющих некоторый промежуток, и
вероятность появления любого конкретного значения равна нулю.
В связи с этим, для описания непрерывных случайных величин
используется другой способ установления соответствия между значениями
случайной величины и вероятностями их появления в виде функции
распределения вероятностей.
Функция распределения вероятностей (или просто функция
распределения) F (x) случайной величины X представляет собой
вероятность того, что случайная величина X примет значение меньшее,
чем некоторое заданное значение x:
F (x) =P(X<x). (2.1)
Функция распределения непрерывной случайной величины X,
принимающей любые значения из некоторого интервала, может быть
представлена:
· аналитически в виде математического выражения (2.1),
отражающего зависимость вероятности от значения случайной величины;
· графически в виде непрерывной функции, отображаю-
щей зависимость (2.1), или в виде гистограммы функции распределения
полученной экспериментально, например в процессе имитационного моделирования, и представляющей собой дискретный график, в
котором по оси абсцисс откладываются частотные интервалы, охватывающие все возможные значения случайной величины, а по оси ординат –
накопленная частота попадания случайной величины в эти частотные
интервалы.
Накопленная частота попадания в i -й частотный интервал
определяется отношением количества случайных величин, значения
которых находятся в интервале (-¥; i x), к общему количеству случайных
величин, полученных в процессе экспериментов.
Свойства функции распределения:
·функция распределения F (x) есть неубывающая функция своего
аргумента, то есть если xj > xi, то F(xj) ³ F (xi)
· F (-¥) = 0;
· F (+¥) = 1.
Если случайная величина определена только в области
положительных значений, ее функция распределения равна нулю на всем
промежутке от минус бесконечности до нуля.
Вероятность того, что случайная величина примет значение из
некоторого интервала (a, b), определяется через функцию распределения
как
P(a < x < b) = F (b) - F (a).
Функция распределения F (x) является универсальной характеристи-
кой случайной величины и существует как для непрерывных, так и для
дискретных величин. Функция распределения дискретной случайной
величины X, принимающей значения x 1, x 2,..., xi,..., определяется как
F(xm)=P(X < xm)= 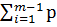 i
i
где pi - вероятность того, что случайная величина X примет значение xi.
На практике вместо функции распределения чаще используют
другой способ представления закона распределения непрерывной
случайной величины в виде плотности распределения вероятностей,
которая в отличие от функции распределения обладает большей
наглядностью и позволяет получить представление о близости того или
иного распределения к одному из известных теоретических распределений,
имеющих аналитическое выражение.
Плотность распределения вероятностей f (x) определяется как
производная от функции распределения F (x) по x:
f(x)=F′(x)=dF(x)/dx
Размерность плотности распределения f (x) обратна размерности
случайной величины, в то время как функция распределения F (x), как
всякая вероятность, есть величина безразмерная.
Плотность распределения непрерывной случайной величины X, как и
функция распределения, может быть представлена:
· аналитически в виде математического выражения y = f (x);
· графически в виде непрерывной функции (графика),
отображающей зависимость y = f (x), или в виде гистограммы
плотности распределения, в которой в отличие от гистограммы функции
распределения по оси ординат откладывается частота (или число)
попаданий случайной величины в каждый из частотных интервалов.
Свойства плотности распределения:
· плотность распределения есть функция неотрицательная: f (x) ³ 0;
· интеграл в бесконечных пределах от плотности распределения
равен единице.
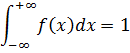
Функция и плотность распределения случайной величины однознач-
но связаны между собой. В частности, функция распределения определяет-
ся через плотность распределения следующим образом:

Тогда вероятность того, что случайная величина примет значение из
некоторого интервала (a, b), может быть определена через плотность
распределения как

Таким образом, закон распределения непрерывной случайной
величины (непрерывный закон распределения) может быть задан в виде:
· функции распределения F (x) случайной величины X, называемой
также интегральным законом распределения;
· плотности распределения f (x) случайной величины X, называемой
также дифференциальным законом распределения.
6. Каковы основные свойства плотности распределения вероятности для
случайной величины и случайного процесса?
7. Что такое "белый”,”квазибелый” и “окрашенный” шум"?
Термин «белый шум» обычно применяется к сигналу, имеющему автокорреляционную функцию, математически описываемую дельта-функцией Дирака по всем измерениям многомерного пространства, в котором этот сигнал рассматривается. Сигналы, обладающие этим свойством, могут рассматриваться как белый шум. Данное статистиче
|
|
|



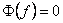 при
при 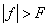 .
.