 |
Рассмотрим два крайних случая
|
|
|
|
1. Полоса пропускания цепи значительно уже спектра сигнала:
;
.
2. Полоса пропускания цепи значительно шире спектра сигнала.
.
10.Какова связь корреляционной функции и спектральной плотности
мощности случайного процесса?
Функция корреляции и спектр мощности стационарного случайного процесса связаны между собой преобразованием Фурье. Поэтому
Данная теорема в теории случайных процессов получила название теоремы Винера-Хинчина.
11.В чём состоит отличие корреляционной и ковариационной функций
случайного процесса?
Ширину спектра сигнала определяет максимальная скорость его изменения. С другой стороны, скорость изменения сигнала определяет и ход ковариационной функции, то есть можно утверждать, что Wx(w) и Kx(t) взаимосвязаны. Эту связь определили независимо друг от друга ученые Н.Винер и А.Я.Хинчин, поэтому ее называют теоремой Винера-Хинчина. Согласно этой теореме энергетический спектр стационарного случайного процесса и его ковариационная функция связаны прямым и обратным преобразованием Фурье, то есть
| (12) |
Для случайных процессов с нулевым средним (mx =0) вместо Kx(t) следует поставить корреляционную функцию Rx(t).
Из этой связи вытекает свойство, аналогичное свойствам преобразований Фурье для детерминированных сигналов: чем шире спектр случайного процесса, тем меньше интервал корелляции, и наоборот.
Для белого шума, имеющего в идеализации бесконечно широкий равномерный спектр W (w) =W 0,
.
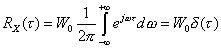где 
- дельта-функция.
Таким образом, такой случайный процесс, как белый шум, имеет корреляционную функцию, равную бесконечности только в точке t = 0, в другие моменты t корреляционная функция равна нулю, поэтому такой шум еще называется дельта -коррелированным процессом.
|
|
|
Если случайный гауссовский процесс с нулевым средним имеет равномерный энергетический спектр в полосе ± w 1 (рис. 1), то его корреляционная функция равна
Рис. 1
Нормированная корреляционная функция будет равна
Если увеличить полосу частот, например в k - раз, то есть 
, то корреляционная функция будет иметь вид
На рис. 2 показаны графики r1 (t) и r2(t) при k = 5.
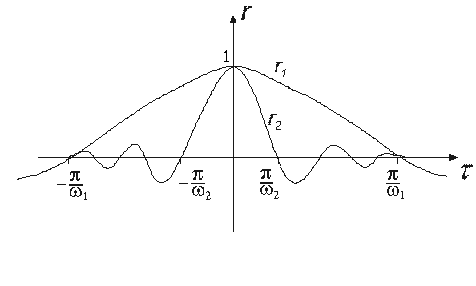
Рис. 2
Пусть энергетический спектр процесса имеет вид узкополосного спектра (рис. 3), причем внутри полосы он равномерен и равен W 3. В этом случае
Нормированная корреляционная функция
изображена на рис. 4
Рис. 4
Огибающая r3(t) по форме подобна функции r1(t), однако имеет вдвое большую протяженность. Высокочастотное заполнение корреляционной функции r3(t) имеет частоту w 0, равную центральной частоте спектра шума. Это говорит о том, что и мгновенное значение шумового колебания изменяется в среднем с частотой w 0 , то есть такое шумовое колебание может быть представлено в виде случайного УПС
где 
- медленно меняющиеся случайные огибающая, фаза и мгновенная частота узкополосного процесса.
12.Как найти взаимную корреляционную функцию случайных процессов на
входе и выходе линейной цепи? (см вопр. 9)
13.Каковы свойства взаимной корреляционной функции двух случайных
процессов?
Во многих случаях представляет интерес вопрос о том, какова статистическая связь между двумя стационарными случайными процессами Х(t) и Y(t). Принять вводить взаимные функции корреляции этих процессов по формулам:
Случайные процессы называются стационарно связанными, если функции
Зависят не от самих аргументов t1и t2 , а лишь от разности 
В этом случае очевидно,
Предположим, что случайные процессы X(t) и Y(t)статистически независимы в том смысле, что для мгновенных значений х = х(t) и 
=y(t+ 
независимо от величины 
двумерная совместная плотность вероятности p(x,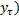 
=p1(x)p2(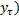. Тогда
|
|
|
) 
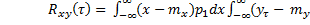Т.е. из статистической независимости случайных процессов вытекает их некоррелированность. Однако в общем случае обратное утверждение не справедливо.
14.Как связаны спектральные плотности мощности случайных процессов на
входе и выходе линейной цепи?
Спектральная плотность мощности на выходе определяется аналогично тому, как это делалось при определении спектра выходного детерминированного сигнала.
Если входной сигнал обладает спектром мощности Wвх(w), то на выходе сигнал будет иметь спектральную плотность мощности
Wвых (w)=Wвх(w) H2(w).
Корреляционную функцию определим как обратное преобразование Фурье
Аналогичные записи можно провести на основе знания импульсной характеристики цепи. Поскольку спектральной функции Wвх(w) соответствует корреляционная функция
а спектральной функции H2(w) соответствует
то произведению Wвх(w) H2(w) соответствует свертка
и
В случае белого шума на входе с Wвх(w)=W0 имеем Wвых(w)= W0H2, а
Это же выражение можно применить и для случая, когда спектральная плотность мощности случайного стационарного процесса на входе цепи равномерна лишь в полосе прозрачности цепи.
15.Что такое автокорреляционная функция импульсной характеристики
линейной цепи? Как и для чего её можно использовать?
При анализе преобразования стационарных случайных процессов линейными цепями известны корреляционная функция или спектральная плотность мощности процесса на входе и
структура цепи (еѐ характеристики). В результате анализа определяются корреляционная функция или спектральная плотность мощности процесса на выходе. Корреляционная функция процесса на выходе цепи определяется как свѐртка корреляционной функции процесса на входе и автокорреляционной функции импульсной характеристики цепи.
вых 
Где 
автокорреляционная функция импульсной характеристики цепи.
Спектральная плотность мощности процесса на выходе цепи может быть определена умножением квадрата АЧХ цепи на спектральную плотность мощности процесса на входе:
Nвых 
Работа 4
1. Какие цепи относятся к нелинейным?
2. Условие безынерционности нелинейного элемента.
|
|
|
3. Какие функции характеризуют БНЭ?
4. Что такое угол отсечки?
5. Условия применимости кусочно-линейной аппроксимации и функций
А.И.Берга.
6. В каких условиях допустима линейная аппроксимация характеристики
БНЭ?
7. В каких случаях целесообразно применение полиномиальной
аппроксимации?
8. Как определить плотность распределения вероятности случайного
процесса на выходе нелинейной цепи, зная нелинейную зависимость и
плотность распределения вероятности исходного случайного процесса?
|
|
|
