 |
Белый случайный процесс (белый шум)
|
|
|
|
Непрерывный во времени случайный процесс w (t), где  , является белым шумом, тогда и только тогда, когда его математическое ожидание и автокорреляционная функция удовлетворяют следующим равенствам соответственно:
, является белым шумом, тогда и только тогда, когда его математическое ожидание и автокорреляционная функция удовлетворяют следующим равенствам соответственно:

 .
.
В других обозначениях, более близких радиофизикам отечественной школы:

 .
.
То есть, это случайный процесс с нулевым математическим ожиданием, имеющий автокорелляционную функцию, являющуюся дельта-функцией Дирака. Такая автокорреляционная функция предполагает следующую спектральную плотность мощности:
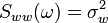
так как преобразование Фурье дельта-функции равно единице на всех частотах. Ввиду того, что спектральная плотность мощности одинакова на всех частотах, белый шум и получил своё название (по аналогии с частотным спектром белого света).
Квазибелым шумом называется случайный процесс n(t), спектр мощности которого равномерен в пределах некоторой полосы частот [-  m,
m,  m], и равен нулю вне этой полосы
m], и равен нулю вне этой полосы
N( )=0,5N0rect (
)=0,5N0rect ( m)
m)
Розовый шум
Спектральная плотность розового шума определяется формулой ~1 / f (плотность обратно пропорциональна частоте), то есть он является равномерно убывающим в логарифмической шкале частот. Например, мощность сигнала в полосе частот между 40 и 60 герц равна мощности в полосе между 4000 и 6000 герц. Спектральная плотность такого сигнала по сравнению с белым шумом затухает на 3 децибела на каждую октаву. Пример розового шума — звук пролетающего вертолёта. Розовый шум обнаруживается, например, в сердечных ритмах, в графиках электрической активности мозга, в электромагнитном излучении космических тел.
Иногда розовым шумом называют любой шум, спектральная плотность которого уменьшается с увеличением частоты
|
|
|
Броуновский (красный, коричневый) шум
Спектральная плотность красного шума пропорциональна 1/f², где f — частота. Это означает, что на низких частотах шум имеет больше энергии, чем на высоких. Энергия шума падает на 6 децибел на октаву. Акустический красный шум слышится как приглушённый, в сравнении с белым или розовым шумом. Может быть получен путем интегрирования белого шума, а также с помощью алгоритма, симулирующего броуновское движение. Спектр красного шума зеркально противоположен спектру фиолетового.
На слух броуновский шум воспринимается более «тёплым», чем белый.
Иногда (обычно в текстах, переведенных с английского языка) этот шум называют также коричневым, слепо переводя фамилию Роберта Броуна (Brown) на русский — причем с английского, хотя Броун был шотландцем. Впрочем, коричневый и красный цвета спектрально весьма близки. Однако в английской Википедии "коричневый" также указан одним из названий данного шума, наряду с броуновским и красным. Коричневый шум не назван в честь спектра мощности, что предполагает коричневый цвет, а, скорее в честь броуновского движения. Красный шум описывает форму спектра мощности, с розовым находясь между красным и белым. Также известен как шум случайных блужданий или шум пьяной ходьбы.
Синий (голубой) шум
Синий шум — вид сигнала, чья спектральная плотность увеличивается на 3 дБ на октаву. То есть его спектральная плотность увеличивается с ростом частоты, и, аналогично белому шуму, на практике он должен быть ограничен по частоте. На слух синий шум воспринимается более резким, нежели белый. Синий шум получается, если продифференцировать розовый шум; их спектры зеркальны
Серый шум
Термин серый шум относится к шумовому сигналу, который имеет одинаковую субъективную громкость для человеческого слуха на всём диапазоне воспринимаемых частот. Спектр серого шума получается, если сложить спектры броуновского и фиолетового шумов. В спектре серого шума виден большой «провал» на средних частотах, однако человеческий слух субъективно воспринимает серый шум как равномерный по спектральной плотности (без преобладания каких-либо частот).
|
|
|
Американский глоссарий Федерального стандарта 1037C по телекоммуникациям даёт определения белому, розовому, синему и чёрному шуму.
Чёрный шум
Термин «чёрный шум» имеет несколько определений:
- Тишина
- Шум со спектром 1/fβ, где β > 2 (Manfred Schroeder, «Fractals, chaos, power laws»). Используется для моделирования различных природных процессов. Считается характеристикой "природных и искусственных катастроф, таких как наводнения, обвалы рынка и т. п. "
- Ультразвуковой белый шум (с частотой более 20 кГц), аналогичный т. н. «черному свету» (с частотами слишком высокими, чтобы его можно было воспринимать, но способному воздействовать на наблюдателя или приборы).
- Шум, спектр которого имеет преимущественно нулевую энергию за исключением нескольких пиков.
8. Как определяется корреляционная функция случайного процесса?
ФУНКЦИЯ КОРРЕЛЯЦИОННАЯ СЛУЧАЙНОГО ПРОЦЕССА
X(t) есть Функция R(t,s) = E[X(t) - m(t)]· (X(s)-m(s)], где m(t) = EX(t) — математическое ожидание X(t). R(t,s) характеризует связь между отдельными точками t и s. Если имеются 2 случайных процесса Х(t) и Y(t) с Ф. к. с. п. Rx (t,s) и RY(t,s) и математическим ожиданием тX (t) и mY (t), to можно определить взаимную корреляционную функцию:
rxy (t,s) = E{X(t) — тX (t)}{Y(s) — mY (s)}. По виду Ф. к. с. п. можно проверить модель случайного процесса и тип динамической системы, его генерирующей. Ф. к. с. п. используется в литологии, в частности, при изучении геол. смысла распределения пористости и выяснении специфики условий осадконакопления.
9. Как связаны между собой корреляционные функции случайных
процессов на входе и выходе линейной цепи?
Пусть на входе четырехполюсника с передаточной функцией  и импульсной характеристикой g(t) действует сигнал
и импульсной характеристикой g(t) действует сигнал  , обладающий спектральной плотностью
, обладающий спектральной плотностью  и автокорреляционой функцией
и автокорреляционой функцией  . Требуется найти автокорреляционную функцию выходного сигнала
. Требуется найти автокорреляционную функцию выходного сигнала  и взаимно корреляционную функцию
и взаимно корреляционную функцию  .
.
 .
.
Произведению спектральных функций соответствует свертка их оригиналов
|
|
|
 , где
, где
 - автокорреляционная функция сигнала на входе.
- автокорреляционная функция сигнала на входе.
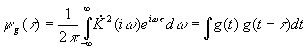 - автокорреляционная функция импульсной характеристики цепи.
- автокорреляционная функция импульсной характеристики цепи.
Найдем взаимно корреляционную функцию выходного и входного сигнала:
 - согласно выражению для спектра взаимно корреляционной функции.
- согласно выражению для спектра взаимно корреляционной функции.
 - комплексно-сопряженная функция
- комплексно-сопряженная функция  . Заменяя
. Заменяя  , получим
, получим 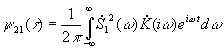 . Произведению двух спектральных функций соответствует свертка оригиналов
. Произведению двух спектральных функций соответствует свертка оригиналов  .
.
|
|
|


