Решение транспортной задачи методом потенциалов

Лабораторная работа №2

Методы принятия решений в условиях определенности

Принятие решения в транспортных задачах

Транспортные задачи, являясь подклассом задач линейного программирования, затрагивают, как правило, распределение ресурсов, находящихся у т производителей (поставщиков), по п потребителям этих ресурсов. К числу таких задач относятся:

– соответствие пунктов отправления и пунктов назначения;

– прикрепление потребителей ресурса к производителям;

– взаимная "привязка" грузопотоков прямого и обратного направлений;

– отдельные задачи оптимальной загрузки промышленного оборудования;

– оптимальное распределение объемов выпуска промышлен­ной продукции между заводами-изготовителями и др.

Рассмотрим модель транспортной задачи на примере прикреп­ления пунктов отправления к пунктам назначения. В т пунктах отправления (А₁ А₂,..., A_m)сосредоточено определенное коли­чество единиц некоторого однородного груза а₁, а₂, а_т . Известно также, что данный груз потребляется в и пунк­тах назначения (В₁, В₂,..., В_m) с объемом потребления b₁ b₂,..., b_n .Известна матрица стоимостей доставки С = (c_ij), где c_ij – расходы на перевозку единицы груза из пункта А_i в пункт В_j. Требуется составить экономико-математическую модель и рас­считать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого /-го пункта (поставщи­ка) в каждый j -й пункт (потребителю) с минимальными тран­спортными издержками.

Обозначим количество груза, перевозимого из пункта А. в пункт В через х_г. Тогда целевая функция задачи будет иметь вид

,

(1.5.1)

а ограничения выглядят следующим образом:

а) все грузы из i -х пунктов должны быть отправлены, т.е. должен быть осуществлен полный вывоз:

(1.5.2)

б) все 7-е пункты (потребители) должны быть обеспечены грузами, т.е. должно иметь место полное удовлетворение спроса:

(1.5.3)

Суммарные объемы отправления должны равняться суммар­ным объемам назначения, т.е. необходимым и достаточным ус­ловием разрешимости задачи является условие баланса:

(1.5.4)

Кроме того, должно выполняться условие неотрицательности переменных:

(1.5.5)

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения 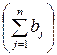, т.е. выполняется равенство (1.5.4). Если такого равенства нет (по­требности выше запасов или наоборот), задачу называют откры­той, т.е.

.

(1.5.6)

Исходные данные можно представить в виде табл. 1.5.1.

Таблица 1.5.1

Поставщики	Потребители	Запасы (объемы отправления)
В1	В2	…	Bn
A1	c11		c12		…	c1n		a1
	x11		x12		x1n
A2	c21		c22		…	c2n		a2
	x21		c22		x2n
…			…		…
Am	cm1		cm2		…	cmn		a3
	xm1		xm2		xmn
Потребитель	b1	b2	…	bn

 

Если дана открытая задача, то ее необходимо привести к закры­той форме. В случае, если потребности по пунктам назначения iпревышают запасы пунктов отправления, то вводится фиктив­ный поставщик с недостающим объемом отправления, а если [запасы поставщиков превышают потребности потребителей, то I вводится фиктивный потребитель с необходимым объемом потребления.

Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.

Транспортным задачам присущи следующие особенности:

· распределению подлежат однородные ресурсы;

· условия задачи описываются только уравнениями;

· все переменные выражаются в одинаковых единицах изме­рения;

· во всех уравнениях коэффициенты при неизвестных равны единице;

· каждая неизвестная встречается только в двух уравнениях системы ограничений.

 

Решение транспортной задачи методом потенциалов

 

Транспортные задачи могут решаться симплекс-методом. Однако, благодаря особенностям переменных задачи и ее ограничений существуют менее, громоздкие методы ее решения. Наиболее распространенным методом является метод потенциалов, при котором для каждой i -й строки (i -му поставщику) устанавлива­ется потенциал u_i, который можно интерпретировать как цену продукта в пункте поставщика, а для каждого столбца j (j -му по­требителю) – потенциал v_j,который можно принять за цену продукта в пункте потребителя. В простейшем случае цена в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е. .

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: