Методом северо-западного угла

 

Определяем элементы матрицы , начиная с верхнего ле­вого угла. Находим величину х₁₁ = тin{а₁, b₂}. Если b₁<a₁, то x₁₁ = b₁, и первый столбец закрыт для расчета остальных элемен­тов, т.е. х_i1 = 0, i = 1, 2, 3,..., т. Если b₁>а₁, то х₁₁ = а₁ и x_1j = 0, j = 1, 2, 3,..., n.

Затем вычисляем x₁₂ = min {a_x – x₁₁ b₂} при a₁>b₁, x₂₁ = min { a₂, b₁–х₁₁ }при а₁<b₁.

Этот процесс продолжается до тех пор, пока на каком-то этапе не исчерпаются ресурсы а_т и не удовлетворятся потребности b_п.

Пример 1. Даны: матрица транспортных издержек , ; объемы производства a_i и объемы истреб­ления b_j.

					ai
C=
bj

 

Проверяем условие баланса ; . Строим исходный опорный план Х_о:

x₁₁ = min{60, 70} = 60;

x₂₁ = min{55, 70-60}= 10;

x₂₂ = min {5, 55- 10}= 5;

x₂₃ = min {45, 55- 10-5} = 40;

x₃₃ = min{40, 45-40} = 5;

x₃₄ = min{70, 40-5}= 35;

x₄₄=35;

.

Полученный план невырожден, так как .

1.5.3. Построение начального опорного плана

Методом минимального элемента

 

Данный метод позволяет получить опорный план с учетом матрицы стоимости перевозок C=|c_ij|. План строим таким об­разом, чтобы перевозки x_ij выполнялись, по возможности, по маршрутам с минимальной стоимостью. Для этого элементы матрицы С (см. исходные данные предыдущего примера) нуме­руем, начиная от минимального в порядке возрастания (показа­но верхним индексом), а затем в этом же порядке определяем элементы матрицы X:

					ai
C=	11	24	916	714
36	410	12	512
613	411	818	39
25	37	38	13
bj

 

(1) x₁₁ = min{60, 70} = 60;

(2) x₂₃=min{55, 45} = 45;

(3) x₄₄=min{35, 70} = 35;

(4) х₁₂= 0;

(5) х₄₁=0;

(6) x₂₁=min{55, 70-60} = 10;

(7) х₄₂= 0;

(8) х₄₃=0;

(9) x₃₄=min{40, 70-35} = 35;

(10) х₂₂=0;

(11) x₃₂=min {40-35, 5} = 5.

Элементы матрицы Х, соответствующие (12), (13), (14), (15), (16), не рассматриваются в силу того, что исчерпаны все ресурсы и удовлетворены все потребности.

Строим опорный план , заполняя в порядке полученной нумерации:

.

Построенный план – невырожденный, поскольку количество ненулевых элементов равно 6, а .

 

Метод потенциалов

 

Рассмотрим работу алгоритма на данных, приведенный в примере 1. Допустим, был получен следующий начальный опорный план:

.

Для удобства вычисления потенциалов и представим графически план перевозок, соответствующий этому начальному опорному плану (см. рис. 1.5.1).

 

Рис. 1.5.1

По соответствующим маршрутам указываем стоимость пере­возки c_ij единицы груза из i -го пункта в j -й. Принимаем u₁ = 0 (можно взять любое число) и, пользуясь соотношением (1.5.8), определяем потенциалы:

Рассчитываем элементы оценочной матрицы по соотноше­нию (1.5.7):

и т.д.

Получаем следующую матрицу:

Так как в С₁ имеются отрицательные элементы, план Х₀ не является оптимальным.

Первая итерация. В матрице Х_о, начиная с элемента х₃₂, соот­ветствующего в оценочной матрице наибольшему по модулю от­рицательному элементу (-7), строим цепочку, в которую входят элементы . Изменяя элементы, входящие в цепочку, на величину q = min{5, 5} = 5 строим новый план Х₁ (см. пп. 2, 3 алгоритма):

,

.

Полученный план является вырожденным. Поскольку в даль­нейших расчетах оперируем невырожденным планом, один из нулей цепочки заменяем величиной . В случае вырожден­ности при построении начального опорного плана вводим по той коммуникации, которая необходима для определения по­тенциалов и .

В матрице вначале отметим подчеркиванием нули, соот­ветствующие базисным переменным плана Х₁, и зачерки­ваем 3-ю строку, содержащую наименьшее значение (-7), затем 4-й столбец, так как 3-я строка на 4-м месте содержит подчерк­нутый элемент, а затем 4-ю строку, так как 4-й столбец содержит подчеркнутый элемент. Имеем:

Затем ко всем элементам зачеркнутых строк прибавляем , а от элементов зачеркнутых столбцов вычитаем . Получаем новую оценочную матрицу С₂:

.

В оценочной матрице С₂ нет отрицательных элементов, следо­вательно, план X₁, является оптимальным. Стоимость перевозок будет равна:

.

Перечислим наиболее часто встречающиеся экономические задачи, которые относятся к транспортным задачам [4, 16, 18].

1. Отдельные поставки от определенных поставщиков неко­торым потребителям должны быть исключены (из-за отсутствия необходимых условий хранения, чрезмерной перегрузки комму­никаций и т.д.). Это ограничение требует, чтобы в матрице пе­ревозок, содержащей оптимальный план, определенные клетки оставались свободными, что достигается искусственным завы­шением затрат c_ij на перевозки. При этом производят завышение величины с_ij, до таких значений, которые будут заведомо больше всех и с которыми их придется сравнивать в процессе решения задачи.

2. На предприятии необходимо определить минимальные суммарные затраты на производство и транспортировку продукции. С подобной задачей сталкиваются при решении вопросов, Связанных с оптимальным размещением производственных проектов. Здесь может оказаться экономически более выгодным доставлять сырье из более отдаленных пунктов, но зато при меньшей его себестоимости. В таких задачах за критерий опти­мальности принимают сумму затрат на производство и транспортировку продукции.

3. Ряд транспортных маршрутов, по которым необходимо доставить грузы, имеет ограничения по пропускной способности. если, например, по маршруту A_iB_i можно провести не более p единиц груза, то В -йстолбец матрицы разбивается на два столбца – и . В первом столбце спрос принимается равным разности между действительным спросом b_j и ограничени­ем р: b' = b_j - p, во втором – равным ограничению р, т.е. 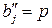. Затраты в обоих столбцах одинаковы и равны, но в первом столбце В' в клетке, соответствующей ограничению i, вместо ис­тинного тарифа c_ij ставится искусственно завышенный тариф М (клетка блокируется). Затем задача решается обычным способом.

4. Поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет. В этом случае уменьшают запас груза у поставщиков и спрос потребителей и решают задачу относительно тех поставок, которые необязательны. Полученное решение корректируют с учетом обязательных поставок.

5. Экономическая задача не является транспортной, но в мате­матическом отношении подобна транспортной, так как описыва­ется аналогичной моделью, например моделью распределения производства изделий между предприятиями, оптимального закрепления механизмов по определенным видам работы.

6. Необходимо максимизировать целевую функцию задачи транспортного типа. В этой ситуации при составлении опорного плана в первую очередь стараются заполнить клетки с наиболее высокими значениями показателей c_ij. Выбор клетки, подлежа­щей заполнению при переходе от одного допустимого плана к другому, должен производиться не по минимальной отрицатель­ной разнице , а по максимальной положительной разнице . Оптимальным будет план, которому в последней таблице сопутствуют свободные клетки с неположи­тельными элементами, т.е. .

7. Необходимо в одно время распределить груз различного рода по потребителям. Задачи данного типа называются много­продуктовыми транспортными задачами. В этих задачах постав­щики т родов грузов разбиваются на т условных поставщиков, а потребители п родов грузов разбиваются на п условных потре­бителей. С учетом этой разбивки составляют полную транспорт­ную таблицу. При этом заметим, что некоторые маршруты должны быть блокированы (закрыты), поскольку в данной по­становке задачи грузы разного рода не могут заменять друг дру­га. Этим маршрутам должна соответствовать очень высокая стоимость перевозки. Многопродуктовую задачу не всегда обяза­тельно описывать одной моделью. Например, если поставки грузов различного рода независимы, то задачу можно предста­вить в виде комплекса транспортных задач по каждому роду гру­за. Однако если между грузами различного рода существует связь (например, одни из грузов можно заменить другими), то в общем случае исходную модель (задачу) не удается разбить на комплекс простых транспортных задач.

Пример 2. Первый сыроваренный завод (A₁) производит сыр двух сортов в следующих количествах: 3 т – I сорта и 4 т – II сорта. Второй сыроваренный завод (А₂) также производит сыр двух сортов в следующих количествах: 5 т – I сорта и 2 т – II сорта. Сыр с заводов должен быть поставлен в два супермар­кета: "РАМСТОР" и "ПЯТЕРОЧКА". В первый (B₁) – 2т сыров I сорта и 3 т – II сорта и остальные 2 т сыра любого сорта. Во второй (В₂) – 8т сыров, в том числе обязательно 1 т – I сорта и 2 т – II сорта.

Стоимость перевозки в дсн. сд. 1 т сыра составляет: из пунк­та A₁ в пункты B₁ и В₂ – 10 и 15 ден. ед. соответственно; из пункта А₂ в пункты В₁и В₂ – 20 и 10 ден. ед. соответственно. Составить оптимальный план перевозок.

Решение. Каждого поставщика (сыроваренные заводы) разби­ваем на две составляющие согласно двум видам сыра ( и ; и ), аналогично потребителей (супермаркеты) разбиваем на три части (потребителей сыра I сорта, II сорта и любого сор­та): , и , а также , и . Потребности превышают запасы, поэтому вводим фиктивного поставщика А₃ с запасом сыра 1 т, перевозки от которого не производятся, т.е. строка таблицы заполняется нулями. В часть клеток таблицы вводим числа М, значения которых намного больше , например, в клетку (1; 2). Это значит, что поставщик не может удовлетво­рить потребителя сыром II сорта за счет имеющегося сыра I сорта.

Тем самым исходная таблица транспортной задачи будет сле­дующей.

Поставщики	Потребители	Запасы сыра, т
B1	B2
A1			M			M
	M			M
A2			M			M
	M			M
A3

 

Пример 3. Имеются три сорта ткани (, и ) в количестве 80, 70 и 50 м², которую используют при пошиве четырех типов курток (, , и ) в количестве 80, 60, 120, 110 штук. Расход ткани на одну куртку составляет: 0,4; 1,0; 0,6; 0,2 м² соответственно, а себестоимость куртки при использовании I-го сорта ткани задается матрицей C:

.

Определить оптимальное распределение ткани.

Решение. Данную задачу, которая по своему экономическому смыслу не является транспортной, можно привести к таковой. Зная количество и расход ткани на одну куртку, можно опреде­лить потребности в ткани каждого сорта:

80∙0,4 = 32 м²,

60∙1,0 = 60 м²,

120∙0,6 = 72 м²,

110∙0,2 = 22 м².

Общие запасы тканей составляют 200 м², а общие потреб­ности – 186 м², поэтому необходимо в таблицу ввести фиктив­ного потребителя В₅ с нулевыми затратами. А так как модель составляется относительно ткани, то исходную матрицу себестоимостей С следует преобразовать относительно единицы ткани (каждый столбец матрицы С разделим на количество ткани, приходящейся на одну куртку).

Исходная таблица будет следующей.

Поставщики	Потребители	Запасы, м2
В1	В2	В3	В4	В5
А1
А2
А3
Потребность, м2

Пример 4. Завод "Калибр" переводит свое производство на выпуск определенного вида изделий, которые будут выпускаться в течение года. Величины спроса в течение года распределяются поквартально и составляют 100, 180, 150 и 200 изделий соответ­ственно. В каждом квартале спрос можно удовлетворить за счет:

• запасов изделий, произведенных в прошлом квартале и со­храняющихся для реализации в будущем;

• производства изделий в течение текущего квартала;

• избытка производства изделий в более поздние кварталы в счет невыполненных заказов.

Затраты на одно изделие в каждом квартале составляют 30 усл. ед. Изделие, произведенное для более поздней реализа­ции, влечет за собой дополнительные издержки на хранение 10 усл. ед. в квартал. С другой стороны, каждое изделие, выпус­каемое в счет невыполненных заказов, облагается штрафом в размере 20 усл. ед. в квартал.

Объем производства изделий меняется от квартала к кварталу в зависимости от выпуска других изделий. В рассматриваемые четыре квартала предполагается выпуск 80, 120, 250 и 200 изде­лий соответственно.

Требуется составить план, имеющий минимальную стоимость производства и хранения изделий.

Решение. Данную задачу можно сформулировать как транс­портную, записав следующую эквивалентность между элемента­ми производственной и транспортной задач.

Транспортная система	Производственная система
1. Исходный пункт i.	1. Период производства i.
2. Пункт назначения j.	2. Период потребления j.
3. Предложение в пункте i.	3. Объем производства за период i.
4. Спрос в пункте j.	4. Реализация за периоду j.
Стоимость перевозки из i и j.	Стоимость производства и хранения за период i и j.

Для рассматриваемой задачи стоимость "перевозки" изделия из периода i в период j выражается как

стоимость производства в i -й период, i=j;

стоимость производства в i -й период плюс стоимость задержки от i до j, i <j;

стоимость производства в i -й период плюс штраф за нарушение срока, i>j.

Таким образом, затраты в период i при реализации продукции в тот же период j (i=j) оцениваются только стоимостью про­изводства. Если производимая в i -й период продукция будет потребляться позже (i < j), то возникают издержки, связанные с хранением. Аналогично, если производство в i -й период не будет выполнено (i>j), то возникают дополнительные расходы в виде штрафа. Например,

Исходная транспортная таблица выглядит следующим образом.

Период потребления	Период производства	Объем производства
Спрос

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: