 |
Решение транспортной задачи средствами
|
|
|
|
Табличного процессора Excel
Требуется решить следующую транспортную задачу. Известны три поставщика с имеющимися у них запасами продукции, четыре потребителя, нуждающиеся в данной продукции и транспортные затраты на поставку продукции от поставщиков к потребителям. Данные представлены в таблице.
| Поставщики | Потребители | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| A3 | |||||
| Потребность |
Необходимо прикрепить поставщиков к потребителям с учетом минимальных транспортных затрат.
Данная задача является закрытой, так как суммарные запасы и потребности в продукции совпадают, т.е.
 .
.
Решение задачи в Excel состоит из следующих шагов:
1) создание формы для ввода условий задачи;
2) ввод исходных данных;
3) определение целевой функции;
4) ввод ограничений и граничных условий;
5) проведение расчетов.
1. Создание формы для ввода условий задачи, ввод исходных данных и определение целевой функции
Создаем матрицу перевозок, которая имеет изменяемые ячейки ВЗ:Е5. После проведения расчетов на ее месте будет записан оптимальный план перевозок. По каждой строке и столбцу матрицы перевозок записываем соответствующую формулу:
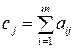 ,
,  .
.
В ячейки A9:F14 введем исходные данные задачи, а в ячейке А15 запишем значение целевой функции, используя функцию =СУММПРОИЗВ(В2:Е5;В11:Е13). Тем самым получим матрицы, как показано на рис. 1.5.2.

Рис. 1.5.2
Ввод ограничений и граничных условий
Устанавливаем курсор на ячейку А15, в которой записано значение целевой функции, и вызываем операцию Поиск решения: Сервис à Поиск решения. В появившемся окне "Поиск решения" в поле Установить целевую функцию следует внести адрес ячейки А15, в которой записано значение целевой функции (см. рис. 1.5.3).
|
|
|

Рис. 1.5.3
Так как решается задача на минимум, то следует установить, что целевая функция будет равной минимальному значению. В поле Изменяя ячейки ввести адреса изменяемых ячеек ВЗ:Е5. После этого следует добавить ограничения, нажав на клавишу Добавить. На экран будет выдано окно "Добавление ограничения" (см. рис. 1.5.4).

Рис. 1.5.4
Все потребности должны быть удовлетворены, т.е.

Аналогично строится ограничение и по запасам, которые должны быть распределены, т.е.
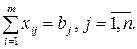
После ввода последнего ограничения вместо нажатия клавиши Добавить необходимо нажать клавишу ОК. На экране появится окно "Поиск решения", как показано на рис. 1.5.3.
Решение задачи
Перед тем как выполнить решение задачи, которое проводится в том же окне "Поиск решения", следует выполнить некоторые назначения, нажав на клавишу Параметры. Например, следует установить флажок Неотрицательные значения и флажок Линейная модель (см. рис. 1.5.5).

Рис. 1.5.5
После проведения всех необходимых установок надо нажать клавишу ОК, что приведет к возврату на окно "Поиск решения". В этом окне следует нажать на клавишу Выполнить, послечего на рабочем поле Excel будет выдан оптимальный план поставок (см. табл. 1.5.2) и диалоговое окно "Результаты поиска решения" (см. рис. 1.5.6), а в ячейке А15 будет выдан результат целевой функции для данной задачи, равный 300.
Таблица 1.5.2

Рис. 1.5.6
ЗАДАНИЕ 3
Имеются три пункта поставки однородного груза  и пять пунктов
и пять пунктов  потребления этого груза. На пунктах
потребления этого груза. На пунктах  находится груз соответственно в количестве
находится груз соответственно в количестве 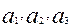 тонн. В пункты
тонн. В пункты  требуется доставить соответственно
требуется доставить соответственно  тонн груза. Затраты на перевозку 1 тонны груза между пунктами поставки и потребления приведены в матрице Д (в рублях).
тонн груза. Затраты на перевозку 1 тонны груза между пунктами поставки и потребления приведены в матрице Д (в рублях).
|
|
|
 ,
,
где  – есть стоимость в рублях перевозки 1 тонны груза от поставщика с номером
– есть стоимость в рублях перевозки 1 тонны груза от поставщика с номером  к потребителю с номером
к потребителю с номером  .
.
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты на перевозки были минимальными.
3.1. 

 .
.
3.2. 
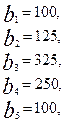
 .
.
3.3.


 .
.
3.4. 

 .
.
3.5. 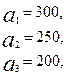

 .
.
3.6. 

 .
.
3.7. 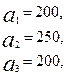

 .
.
3.8. 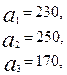

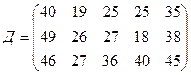 .
.
3.9. 

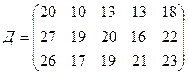 .
.
3.10. 

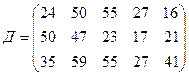 .
.
3.11. 

 .
.
3.12. 
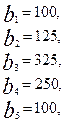
 .
.
3.13. 

 .
.
3.14. 

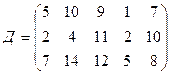 .
.
3.15. 

 .
.
3.16. 

 .
.
3.17. 

 .
.
3.18. 

 .
.
3.19. 

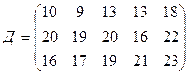 .
.
3.20. 

 .
.
3.21. 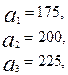

 .
.
3.22. 
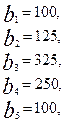
 .
.
3.23. 

 .
.
3.24. 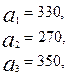

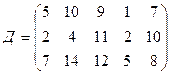 .
.
3.25. 

 .
.
3.26. 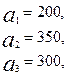

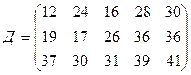 .
.
3.27. 

 .
.
3.28. 

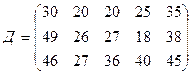 .
.
3.29.. 

 .
.
3.30. 

 .
.
Варианты заданий для решения транспортных задач
1. В пунктах А и В находятся соответственно 110 и 190 т горючего. Пунктам 1, 2, 3 требуются соответственно 70, 90, 140 т горючего. Стоимость перевозки 1 т горючего из пункта А в пункты 1, 2, 3 равна 200, 300, 400 руб. за 1 т соответственно, а из пункта В в пункты 1, 2, 3 – 600, 200, 500 тыс. руб. за 1 т соответственно. Составьте план перевозок горючего, минимизирующий общую сумму транспортных расходов.
2. Три завода выпускают станки, которые отправляются четырем потребителям. Первый завод поставляет 60 станков, второй – 70 станков, третий – 20 станков. Станки следует поставить потребителям следующим образом: первому – 40 шт., второму – 30, третьему – 30, четвертому – 50 шт. Стоимость перевозки одного станка от поставщика до потребителя указана в следующей таблице (в ден. ед.).
| Заводы | Потребители | |||
| I | ||||
| II | ||||
| III |
Составьте оптимальный план доставки станков.
3. Для строительства 3-х участков дорожной магистрали необходимо завозить песок. Песок может быть поставлен из 4-х карьеров. Перевозка песка из карьеров до участков осуществляется грузовиками одинаковой грузоподъемности. Расстояние в километрах от карьеров до участков, наличие песка в карьерах и потребность песка на участках дороги приведены в следующей таблице.
| Песчаные карьеры | Участки дороги | Наличие песка, тыс. т | |||
| I | II | III | IV | ||
| I | |||||
| II | |||||
| III | |||||
| Потребность в песке, тыс. т |
Составьте план перевозок, минимизирующий общий пробег грузовиков.
4. Груз, хранящийся на трех складах, необходимо развести по 5-ти магазинам. Для перевозки грузов требуются 40, 30, 35 автомашин соответственно. Первому магазину требуется 20 машин груза, второму – 34, третьему – 16, четвертому – 10 и пятому – 25 машин. Стоимость пробега одной автомашины за 1 км составляет 5 ден. ед. Расстояния от складов до магазинов указаны в следующей таблице.
|
|
|
| Склады | Магазины | ||||
| I | |||||
| II | |||||
| III |
Составьте оптимальный по стоимости план перевозки груза от складов до магазинов.
5. На четырех элеваторах А, В, С, D находится зерно в количестве 100, 120, 150, 130 т, которое нужно доставить на четыре сельскохозяйственных предприятия для посева. Предприятию 1 необходимо поставить 140 т, предприятию 2 – 130, предприятию 3 – 90, предприятию 4 – 140 т зерна. Стоимость доставки потребителям от поставщиков представлена в таблице.
| Элеваторы | Сельскохозяйственные предприятия | |||
| I | II | III | IV | |
| А | ||||
| В | ||||
| С | ||||
| D |
Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки.
6. Деревообрабатывающий комбинат имеет три цеха: А, В, С и четыре склада: 1, 2, 3, 4. Цеха и склады находятся на разных территориях.
Цех А производит 40 тыс. м3 материала, цех В – 30; цех С – 20 тыс. м3 материала. Пропускная способность складов за то же время характеризуется следующими показателями: склад 1 – 30 тыс. м3 материала, склад 2 – 25; склад 3 – 15 и склад 4 – 20 тыс. м3 материала. Стоимость перевозки 1 м3 материала из цеха А на склады 1, 2, 3, 4 соответственно: 10, 20, 60, 40 ден. ед., из цеха В – соответственно 30, 10, 30, 20, а из цеха С – соответственно 50, 70, 50, 10 ден. ед.
Составьте план перевозки изделий, при котором расходы на перевозку 90 тыс. м3 материала были бы наименьшими.
7. В области имеется пять кирпичных заводов, объем выпуска которых в сутки равен 105, 50, 80, 20, 25 т соответственно. Заводы удовлетворяют потребности шести строительных фирм соответственно в количестве 80, 43, 10, 17, 50, 30 т. Оставшийся кирпич отправляют по железной дороге в другие области. Кирпич на строительные объекты внутри области доставляется автомобильным транспортом. Расстояние в километрах от заводов до объектов приведено в таблице.
|
|
|
| Кирпичные заводы | Строительные фирмы | |||||
| Ф1 | Ф2 | Ф3 | Ф4 | Ф5 | Ф6 | |
Определите, с каких заводов и каким фирмам должен доставляться кирпич, а также какие заводы и в каком количестве должны отправлять кирпич в другие области, чтобы транспортные издержки по доставке кирпича автотранспортом были минимальными. Стоимость перевозки 1 т кирпича автотранспортом удовлетворяет условию c = a + d(l - 1), где a =30 ден. ед., d=10 ден. ед., l – пробег, км.
8. Аудиторская фирма, имеющая три подразделения, находящихся в разных местах города, оказывает аудиторские услуги трем предприятиям "Сокол", "Динамо", "Стрела". При этом руководящее звено названных предприятий должно приезжать в фирму для оказания услуг. Производственные мощности фирмы, стоимость услуг подразделений, временные затраты на проезд от предприятия до фирмы и обратно и прогнозируемое количество посещений в квартале приведены в таблице.
| Подразделения фирмы | Производственная мощность, чел. | Стоимость услуг, усл. ед. | Время проезда | ||
| "Сокол" | "Динамо" | "Стрела" | |||
| Требуемое кол-во посещений |
Требуется определить, какое количество посещений должно быть от каждого предприятия в каждое из подразделений, чтобы суммарные расходы на услуги и проезд были минимальными.
9. Завод выпускает продукцию в четырех цехах: А, В, С, D, расположенных на разных территориях. Свою продукцию завод поставляет в шесть магазинов города. Цех А производит130 тыс. шт. изделий, цех В – 90; цех С – 100 и цех D – соответственно 140 тыс. шт. изделий. Плановая потребность магазинов в продукции завода следующая: магазин 1 – 110 тыс. шт. изделий; магазин 2 – 50 тыс. шт.; магазин 3 – 30 тыс. шт., магазин 4 – 80 тыс. шт., магазин 5 – 100 тыс. шт. и магазин 6 – 90 тыс. шт. изделий. Стоимость перевозки 1 тыс. шт. изделий из цехов в магазины приведена в таблице.
| Цеха завода | Магазины | |||||
| М1 | M2 | M3 | M4 | M5 | M6 | |
| А | ||||||
| В | ||||||
| С | ||||||
| D |
Составьте такой план перевозки изделий, при котором расходы на перевозку изделий были бы наименьшими.
10. Четыре растворных узла поставляют раствор четырем строительным фирмам. Для перевозки раствора используются однотипные автомашины. Объем производства растворных узлов в день равен 30, 20, 40, 50 т. Потребности строительных фирм в день: 35, 20, 55, 30 т.
|
|
|
Расстояние в километрах от растворных узлов до строительных объектов указано в таблице.
| Растворный узел | Строительные фирмы | |||
| I | ||||
| II | ||||
| III | ||||
| IV |
Определите, в каком объеме, с каких растворных узлов и куда должен доставляться раствор, чтобы транспортные издержки по его доставке автотранспортом были минимальными.
11. В районе имеются четыре станции технического обслуживания (СТО) машин фирмы "ВОЛЬВО". Основными потребителями их ремонтных услуг являются пять автопредприятий. Производственные мощности СТО, стоимость их услуг, затраты на транспортировку от автопредприятий на СТО и обратно и прогнозируемое количество ремонтов в планируемом периоде на каждом автопредприятии приведены в следующей таблице.
| СТО | Стоимость рем. часа, усл. ед. | Затраты на транспортировку | Производственные мощности | ||||
| П1 | П2 | П3 | П4 | П5 | |||
| Кол-во ремонтов |
Требуется определить, какое количество автомашин из каждого автопредприятия необходимо отремонтировать на каждой СТО, чтобы суммарные расходы на ремонт и транспортировку были минимальными.
12. Имеются четыре овощехранилища, расположенные в разных районах города, в которых сосредоточено 10, 20, 35 и 45 т овощей соответственно. Овощи необходимо перевезти четырем потребителям соответственно в количестве 25, 30, 40 и 15 т. Расстояния от хранилищ до потребителей следующие:
| Хранилище | Потребители | |||
| I | ||||
| II | ||||
| III | ||||
| IV |
Затраты на перевозку 1 т овощей на 1 км постоянны и равны 20 руб.
Определите план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов.
13. Завод имеет три дочерних предприятия, расположенные в разных районах города, по ремонту и обслуживанию холодильных установок в 4-х овощехранилищах. Предприятия в течение года используют следующие мощности по обслуживанию овощехранилищ: 45, 35 и 60 чел. соответственно. Плановые потребности овощехранилищ в услугах предприятий составляют соответственно 20, 35, 40 и 45 чел. Расстояния от предприятий до овощехранилищ следующие:
| Хранилище | Потребители | |||
| I | ||||
| II | ||||
| III |
В стоимость обслуживания одним человеком входит фиксированная сумма ремонта в размере 100 усл. ед. и транспортные расходы в размере 10 усл. ед. за 1 км.
Определите план обслуживания, чтобы суммарные расходы на ремонт и транспортировку были минимальными.
14. Торговая фирма "Весна и осень" включает четыре предприятия и шесть складов в различных регионах страны. Каждый месяц предприятия фирмы производят 100, 15, 90 и 55 ед. продукции. Вся производимая продукция направляется на склады, вместимость которых следующая: 30, 40, 55, 80, 45 и 10 ед. продукции. Издержки транспортировки продукции от предприятий до складов следующие (ден. ед.):
| Предприятия фирмы "Весна и осень" | Склады | |||||
Распределите план перевозок из условия минимизации ежемесячных расходов на транспортировку.
15. Три хлебных комбината с производственными мощностями 130, 110, 80 т хлебобулочных изделий в сутки поставляют свою продукцию в 5 магазинов города. Потребность в хлебобулочных изделиях магазинов следующая: 60, 40, 50, 80, 90 т. Издержки транспортировки продукции от хлебных комбинатов до магазинов следующие (ден. ед.):
| Хлебные комбинаты | Магазины | ||||
| I | |||||
| II | |||||
| III |
Распределите план перевозок из условия минимизации ежедневных расходов на транспортировку.
16. Четыре растворных узла потребляют в сутки 170, 190, 230 и 150 т песка, который отгружается с трех песчаных карьеров. Суточная производительность карьеров равна соответственно 280, 240 и 270 т песка.
Карьеры взимают плату за погрузку песка каждые сутки не с количества отгруженного материала, а "с факта" его отгрузки, куда входит стоимость погрузки, цена песка и транспортные расходы доставки потребителю при закреплении его за карьером. Стоимость перевозки 1 т песка от карьеров до растворных узлов приведены в таблице.
| Растворные узлы | Карьеры | ||
| Цена 1 т песка, руб. | |||
| Суточная стоимость погрузки, руб. |
Найти оптимальный вариант закрепления растворных узлов за карьерами.
17. Потребность области в азотных удобрениях составляет 180 тыс. т в год. Поставку азотных удобрений могут осуществлять три завода со следующими мощностями: 200, 175 и 225 т удобрений в квартал. Потребителями азотных удобрений в области являются 5 агропромышленных фирм. Их потребности в удобрениях следующие: 100, 130, 80, 190 и 100 т в квартал. Транспортные затраты на поставку удобрений с заводов в агрофирмы представлены в таблице.
| Заводы | Агропромышленные фирмы | ||||
| I | |||||
| II | |||||
| III |
Найти оптимальный план поставки удобрений с минимальными транспортными издержками.
18. Три молочных фермы с суточным производством 40, 25 и 35 тыс. л молока снабжают четыре молокозавода, спрос у которых: 15, 40, 30 и 15 тыс. л молока в сутки. Молоко доставляется на заводы молоковозами, одинаковыми по вместимости. Стоимость провоза молока молоковозом на расстояние 1 км составляет 3 ден. ед. Ферма 2 не связана с молокозаводом 4. Расстояние от ферм до молокозаводов следующее:
| Молочные фермы | Молокозаводы | |||
| I | ||||
| II | ||||
| III |
Найти оптимальный план поставки молока с ферм на молокозаводы с минимальными транспортными издержками. Рассчитайте стоимость доставки молока от каждой фермы до молокозавода.
19. Четыре бензохранилища с суточным объемом хранения 60, 40, 100 и 50 тыс. т авиационного бензина снабжают пять аэропортов, спрос на бензин у которых составляет 30, 80, 65, 35 и 40 тыс. т бензина в сутки. Бензин транспортируется в аэропорты одинаковыми по вместимости бензозаправщиками. Стоимость провоза бензина бензозаправщиком на расстояние 1 км составляет 7 ден. ед. Бензохранилище 2 не связано с аэропортом 5, а 3-е бензохранилище не связано с 1-м аэропортом. Расстояние от бензохранилищ до аэропортов следующее:
| Бензохранилища | Аэропорты | ||||
| I | |||||
| II | |||||
| III | |||||
| IV |
Найти оптимальный план поставки бензина с минимальными транспортными издержками. Рассчитайте стоимость доставки бензина от каждого аэропорта до хранилища.
20. Пусть в задаче 1.5.19 объем хранения бензина в хранилище 1 снизился до 20 тыс. т. Кроме того, обязательно условие полного удовлетворения спроса на бензин для аэропорта 3. Недопоставки в аэропорты 2 и 4 штрафуются на сумму 10 ден. ед. за каждую тонну.
Сформулируйте соответствующую транспортную задачу и решите ее на минимум издержек.
|
|
|


