Задача на составление рациональных смесей

Пусть фирма имеет возможность готовить различные виды смесей (продуктов) из закупаемых различных видов сырья. Каж­дый вид сырья содержит разное количество питательных компо­нентов (ингредиентов).

Установлено, что продукция должна удовлетворять по край­ней мере некоторым минимальным требованиям с точки зрения питательности (полезности). Перед руководством фирмы стоит задача определить количество каждого i -го сырья, образующего смесь минимальной стоимости при соблюдении требований к общему расходу смеси и ее питательности.

Введем условные обозначения: – количество i -го сырья в смеси; т – количество видов сырья; п – количество ингредиен­тов в сырье; а_ij – количество i -го ингредиента, содержащегося в единице j -го вида сырья; bj – минимальное количество i -го ингредиента, содержащегося в единице смеси; c_i – стоимость единицы i -го сырья; q – минимальный вес смеси.

В общем виде задача может быть записана

(1.2.10)

при следующих ограничениях:

(1.2.11)

– на общий расход смеси;

(1.2.12)

– на питательность смеси;

(1.2.13)

– на неотрицательность переменных.

Пример 1. Для жизнедеятельности человека среднего возраста ежедневно необходимо потреблять 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных ве­ществ, содержащихся в 1 кг продуктов питания, а также стои­мость этих продуктов в магазине приведены в табл. 1.4. Требуется составить суточный рацион, содержащий не менее указанных выше необходимых питательных веществ и обеспечивающий минимальную общую стоимость закупаемых продуктов.

Таблица 1.4

Питательные вещества	Содержание питательных веществ в 1 кг продуктов, г
	Мясо	Рыба	Масло	Картофель	Сыр	Крупа
Белки
Жиры
Углеводы
Минеральные соли
Стоимость 1 кг продукта, руб.

Обозначим через x_v х,,..., х₆ количество покупаемого каждого вида продукта. Тогда целевая функция данной задачи – обеспече­ние минимальных затрат на покупку продуктов питания – будет записана в виде

F = 70x₁+ 100х₂+60х₃+ 15х₄+ 150х₅+ 20х₆ à min

при следующих ограничениях:

Еще один класс моделей, аналогичных рассмотренным выше, возникает при решении экономической проблемы, связанной с изготовлением смесей различных жидкостей с целью получения пользующихся спросом готовых продуктов.

Представим себе фирму, торгующую различного рода про­дуктами, каждый из которых является смесью нескольких ком­понентов. Предположим, что эта фирма планирует изготовление смесей т видов. Обозначим через количество литров i -го ком­понента, используемого для получения j -го продукта. Тогда пер­вая группа ограничений относится к объемам потребляемых компонентов:

,

где S_i – объем i -го компонента, которым располагает фирма в начале планируемого периода.

Вторая группа ограничений отражает требование, заключаю­щееся в том, чтобы запланированный выпуск продукции хотя бы в минимальной степени удовлетворял имеющийся спрос на каждый из производимых продуктов, т.е.

,

где D_j – минимальный спрос на продукцию j в течение плани­руемого периода.

Третья группа ограничений связана с технологическими осо­бенностями, которые необходимо принимать во внимание при приготовлении смеси. Например, отношение между объемами двух компонентов в процессе получения j -го продукта выглядит так:

, или .

где r – некоторая заданная константа.

Обозначив через доход с единицы продукции x_ij, запишем целевую функцию:

Пример 2. Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содер­жание серы в нем – не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в табл. 1.5.

Таблица 1.5

Характеристика	Компонент автомобильного бензина
№1	№2	№ 3	№4
Октановое число
Содержание серы, %	0,35	0,35	0,3	0,2
Ресурсы, т
Себестоимость, ден. ед. за т

Требуется определить, сколько тонн каждого компонента сле­дует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной.

Целевая функция данной задачи записывается в виде

Первое ограничение по октановому числу:

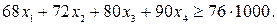
Второе ограничение по содержанию серы:

Приведем ограничения по используемым ресурсам:

Последнее ограничение должно быть на неотрицательность введенных переменных, т.е.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: